Out of Boundary Paths Problem

Problem

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 10^9 + 7.

Examples

Example 1:

1
2
3
4

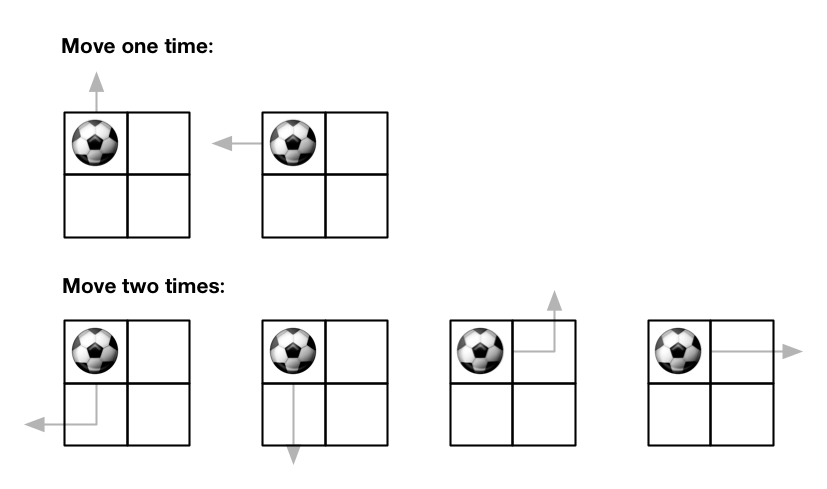
Input:
m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output:
 6

Example 2:

1
2
3
4

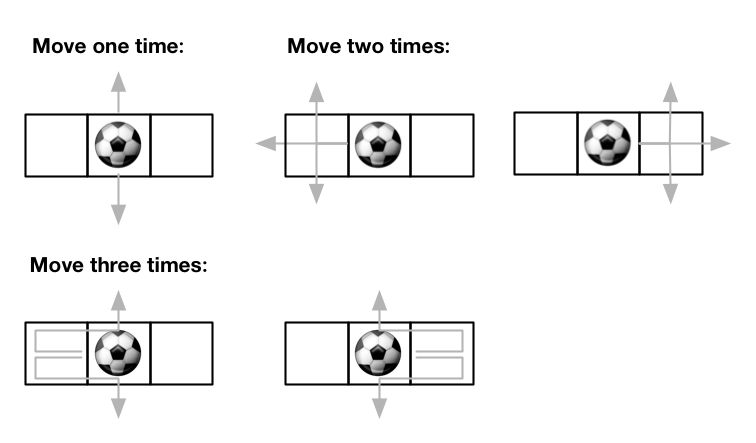
Input:
m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output:
 12

Solution

Method 1 – Dynamic Programming (Top-Down Memoization) 1

Intuition

We use dynamic programming to count the number of ways to move the ball out of the grid. For each position and move count, we recursively try all four directions, and use memoization to avoid recomputation.

Approach

  1. Define a recursive function dp(move, row, col) that returns the number of ways to move the ball out of the grid from position (row, col) with move moves left.
  2. If the ball is out of bounds, return 1.
  3. If no moves left, return 0.
  4. Use memoization to cache results for each (move, row, col).
  5. Try all four directions (up, down, left, right) and sum the results.
  6. Start the recursion from the initial position and maxMove.

Code

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
public:
    int MOD = 1e9 + 7;
    int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        vector<vector<vector<int>>> memo(maxMove+1, vector<vector<int>>(m, vector<int>(n, -1)));
        function<int(int,int,int)> dp = [&](int move, int r, int c) {
            if (r < 0 || r >= m || c < 0 || c >= n) return 1;
            if (move == 0) return 0;
            if (memo[move][r][c] != -1) return memo[move][r][c];
            int ans = 0;
            ans = (ans + dp(move-1, r-1, c)) % MOD;
            ans = (ans + dp(move-1, r+1, c)) % MOD;
            ans = (ans + dp(move-1, r, c-1)) % MOD;
            ans = (ans + dp(move-1, r, c+1)) % MOD;
            return memo[move][r][c] = ans;
        };
        return dp(maxMove, startRow, startColumn);
    }
};
Go
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

func findPaths(m, n, maxMove, startRow, startColumn int) int {
    MOD := int(1e9 + 7)
    memo := make([][][]int, maxMove+1)
    for i := range memo {
        memo[i] = make([][]int, m)
        for j := range memo[i] {
            memo[i][j] = make([]int, n)
            for k := range memo[i][j] {
                memo[i][j][k] = -1
            }
        }
    }
    var dp func(move, r, c int) int
    dp = func(move, r, c int) int {
        if r < 0 || r >= m || c < 0 || c >= n {
            return 1
        }
        if move == 0 {
            return 0
        }
        if memo[move][r][c] != -1 {
            return memo[move][r][c]
        }
        ans := 0
        ans = (ans + dp(move-1, r-1, c)) % MOD
        ans = (ans + dp(move-1, r+1, c)) % MOD
        ans = (ans + dp(move-1, r, c-1)) % MOD
        ans = (ans + dp(move-1, r, c+1)) % MOD
        memo[move][r][c] = ans
        return ans
    }
    return dp(maxMove, startRow, startColumn)
}
Java
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    int MOD = 1000000007;
    Integer[][][] memo;
    public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
        memo = new Integer[maxMove+1][m][n];
        return dp(maxMove, startRow, startColumn, m, n);
    }
    int dp(int move, int r, int c, int m, int n) {
        if (r < 0 || r >= m || c < 0 || c >= n) return 1;
        if (move == 0) return 0;
        if (memo[move][r][c] != null) return memo[move][r][c];
        int ans = 0;
        ans = (ans + dp(move-1, r-1, c, m, n)) % MOD;
        ans = (ans + dp(move-1, r+1, c, m, n)) % MOD;
        ans = (ans + dp(move-1, r, c-1, m, n)) % MOD;
        ans = (ans + dp(move-1, r, c+1, m, n)) % MOD;
        return memo[move][r][c] = ans;
    }
}
Kotlin
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    val MOD = 1000000007
    lateinit var memo: Array<Array<Array<Int?>>>
    fun findPaths(m: Int, n: Int, maxMove: Int, startRow: Int, startColumn: Int): Int {
        memo = Array(maxMove+1) { Array(m) { Array<Int?>(n) { null } } }
        return dp(maxMove, startRow, startColumn, m, n)
    }
    fun dp(move: Int, r: Int, c: Int, m: Int, n: Int): Int {
        if (r < 0 || r >= m || c < 0 || c >= n) return 1
        if (move == 0) return 0
        memo[move][r][c]?.let { return it }
        var ans = 0
        ans = (ans + dp(move-1, r-1, c, m, n)) % MOD
        ans = (ans + dp(move-1, r+1, c, m, n)) % MOD
        ans = (ans + dp(move-1, r, c-1, m, n)) % MOD
        ans = (ans + dp(move-1, r, c+1, m, n)) % MOD
        memo[move][r][c] = ans
        return ans
    }
}
Python
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

def findPaths(m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
    MOD = 10**9 + 7
    from functools import lru_cache
    @lru_cache(None)
    def dp(move: int, r: int, c: int) -> int:
        if r < 0 or r >= m or c < 0 or c >= n:
            return 1
        if move == 0:
            return 0
        ans = 0
        ans = (ans + dp(move-1, r-1, c)) % MOD
        ans = (ans + dp(move-1, r+1, c)) % MOD
        ans = (ans + dp(move-1, r, c-1)) % MOD
        ans = (ans + dp(move-1, r, c+1)) % MOD
        return ans
    return dp(maxMove, startRow, startColumn)
Rust
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

impl Solution {
    pub fn find_paths(m: i32, n: i32, max_move: i32, start_row: i32, start_column: i32) -> i32 {
        const MOD: i32 = 1_000_000_007;
        use std::collections::HashMap;
        fn dp(move: i32, r: i32, c: i32, m: i32, n: i32, memo: &mut HashMap<(i32,i32,i32),i32>) -> i32 {
            if r < 0 || r >= m || c < 0 || c >= n { return 1; }
            if move == 0 { return 0; }
            if let Some(&v) = memo.get(&(move,r,c)) { return v; }
            let mut ans = 0;
            ans = (ans + dp(move-1, r-1, c, m, n, memo)) % MOD;
            ans = (ans + dp(move-1, r+1, c, m, n, memo)) % MOD;
            ans = (ans + dp(move-1, r, c-1, m, n, memo)) % MOD;
            ans = (ans + dp(move-1, r, c+1, m, n, memo)) % MOD;
            memo.insert((move,r,c), ans);
            ans
        }
        let mut memo = HashMap::new();
        dp(max_move, start_row, start_column, m, n, &mut memo)
    }
}
TypeScript
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

class Solution {
    findPaths(m: number, n: number, maxMove: number, startRow: number, startColumn: number): number {
        const MOD = 1e9 + 7;
        const memo: number[][][] = Array.from({length: maxMove+1}, () => Array.from({length: m}, () => Array(n).fill(-1)));
        const dp = (move: number, r: number, c: number): number => {
            if (r < 0 || r >= m || c < 0 || c >= n) return 1;
            if (move === 0) return 0;
            if (memo[move][r][c] !== -1) return memo[move][r][c];
            let ans = 0;
            ans = (ans + dp(move-1, r-1, c)) % MOD;
            ans = (ans + dp(move-1, r+1, c)) % MOD;
            ans = (ans + dp(move-1, r, c-1)) % MOD;
            ans = (ans + dp(move-1, r, c+1)) % MOD;
            memo[move][r][c] = ans;
            return ans;
        };
        return dp(maxMove, startRow, startColumn);
    }
}

Complexity

  • ⏰ Time complexity: O(maxMove * m * n), since each state is computed once.
  • 🧺 Space complexity: O(maxMove * m * n), for memoization table.