problemmediumalgorithmsleetcode-276leetcode 276leetcode276

Pain Fence

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are painting a fence of n posts with k different colors. You must paint the posts following these rules:

  • Every post must be painted exactly one color.
  • There cannot be three or more consecutive posts with the same color.

Given the two integers n and k, return the number of ways you can paint the fence.

Examples

Example 1

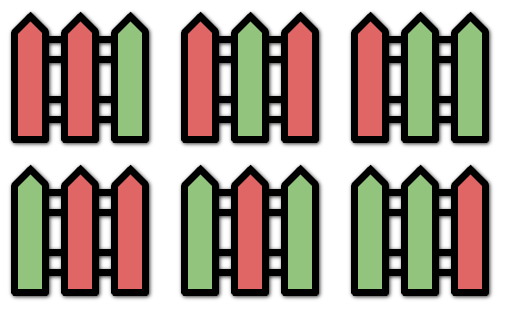
Input: n = 3, k = 2
Output: 6
Explanation: All the possibilities are shown.
Note that painting all the posts red or all the posts green is invalid because there cannot be three posts in a row with the same color.

Example 2

Input: n = 1, k = 1
Output: 1

Example 3

Input: n = 7, k = 2
Output: 42

Solution

Method 1 - Bottom Up DP

Intuition

Use dynamic programming to count the number of ways to paint the fence such that no more than two adjacent posts have the same color. Track two states: painting the current post the same color as the previous (but not the one before that), and painting it a different color.

Approach

Let same be the number of ways to paint the current post the same color as the previous, and diff be the number of ways to paint it a different color. Initialize for the first two posts, then iterate for the rest, updating the states.

Code

C++
class Solution {
public:
    int numWays(int n, int k) {
        if (n == 0) return 0;
        if (n == 1) return k;
        int same = 0, diff = k;
        for (int i = 2; i <= n; ++i) {
            int new_same = diff;
            int new_diff = (same + diff) * (k - 1);
            same = new_same;
            diff = new_diff;
        }
        return same + diff;
    }
};
Go
func numWays(n int, k int) int {
    if n == 0 {
        return 0
    }
    if n == 1 {
        return k
    }
    same, diff := 0, k
    for i := 2; i <= n; i++ {
        newSame := diff
        newDiff := (same + diff) * (k - 1)
        same, diff = newSame, newDiff
    }
    return same + diff
}
Java
public int numWays(int n, int k) {
    if (n == 0) return 0;
    if (n == 1) return k;
    int same = 0, diff = k;
    for (int i = 2; i <= n; i++) {
        int newSame = diff;
        int newDiff = (same + diff) * (k - 1);
        same = newSame;
        diff = newDiff;
    }
    return same + diff;
}
Kotlin
fun numWays(n: Int, k: Int): Int {
    if (n == 0) return 0
    if (n == 1) return k
    var same = 0
    var diff = k
    for (i in 2..n) {
        val newSame = diff
        val newDiff = (same + diff) * (k - 1)
        same = newSame
        diff = newDiff
    }
    return same + diff
}
Python
class Solution:
    def numWays(self, n: int, k: int) -> int:
        if n == 0:
            return 0
        if n == 1:
            return k
        same, diff = 0, k
        for _ in range(2, n+1):
            new_same = diff
            new_diff = (same + diff) * (k - 1)
            same, diff = new_same, new_diff
        return same + diff
Rust
impl Solution {
    pub fn num_ways(n: i32, k: i32) -> i32 {
        if n == 0 { return 0; }
        if n == 1 { return k; }
        let mut same = 0;
        let mut diff = k;
        for _ in 2..=n {
            let new_same = diff;
            let new_diff = (same + diff) * (k - 1);
            same = new_same;
            diff = new_diff;
        }
        same + diff
    }
}
TypeScript
function numWays(n: number, k: number): number {
    if (n === 0) return 0;
    if (n === 1) return k;
    let same = 0, diff = k;
    for (let i = 2; i <= n; i++) {
        const newSame = diff;
        const newDiff = (same + diff) * (k - 1);
        same = newSame;
        diff = newDiff;
    }
    return same + diff;
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of posts.
  • 🧺 Space complexity: O(1), constant space for state variables.

Comments