Painting a Grid With Three Different Colors

Problem

You are given two integers m and n. Consider an m x n grid where each cell is initially white. You can paint each cell red, green, or blue. All cells must be painted.

Return the number of ways to color the grid with no two adjacent cells having the same color. Since the answer can be very large, return it modulo 10^9 + 7.

Examples

Example 1:

Input: m = 1, n = 1
Output: 3
Explanation: The three possible colorings are shown in the image above.

Example 2:

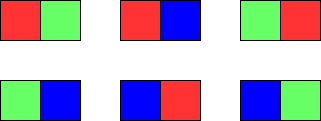
Input: m = 1, n = 2
Output: 6
Explanation: The six possible colorings are shown in the image above.

Example 3:

Input: m = 5, n = 5
Output: 580986

Constraints:

• 1 <= m <= 5
• 1 <= n <= 1000

Solution

Method 1 - Using Dynamic Programming

To solve this problem, we use dynamic programming with state compression. Here's a detailed explanation of the approach:

1. Problem Analysis:
   • We need to calculate the number of valid ways to colour an m x n grid such that no two adjacent cells (vertically or horizontally) have the same colour.
   • Colours are limited to red, green, and blue.
2. Key Insight:
   • For a fixed number of rows m, we can precompute all valid row patterns where no two adjacent cells in a row have the same colours.
   • To transition from one column to another, we compute which row patterns are valid to follow a given row pattern in terms of maintaining "no adjacent colour conflict" vertically.
3. Dynamic Programming:
   • Let prev represent the row pattern for column j - 1 and curr represent the row pattern for column j.
   • We calculate the number of ways to assign valid colours column by column, keeping track of compatible row patterns between adjacent columns.
4. Modulo Operation: Since the result can be large, we compute the result modulo 10^9 + 7.

Code

Java

class Solution {

    public int colorTheGrid(int m, int n) {
        final int MOD = 1000000007;

        // List to store all valid row patterns
        List<Integer> patterns = new ArrayList<>();
        generatePatterns(m, 0, 0, patterns);

        // Number of patterns
        int k = patterns.size();

        // Build compatibility list
        boolean[][] compatible = new boolean[k][k];
        for (int i = 0; i < k; i++) {
            for (int j = 0; j < k; j++) {
                compatible[i][j] = isCompatible(
                    patterns.get(i),
                    patterns.get(j),
                    m
                );
            }
        }

        // DP array
        int[] dp = new int[k];
        Arrays.fill(dp, 1);

        // Transition for each column
        for (int col = 1; col < n; col++) {
            int[] newDp = new int[k];
            for (int i = 0; i < k; i++) {
                for (int j = 0; j < k; j++) {
                    if (compatible[i][j]) {
                        newDp[i] = (newDp[i] + dp[j]) % MOD;
                    }
                }
            }
            dp = newDp;
        }

        // Sum up all the ways to paint the grid
        int ans = 0;
        for (int x : dp) {
            ans = (ans + x) % MOD;
        }
        return ans;
    }

    // Helper method to generate valid patterns for a single column
    private void generatePatterns(
        int m,
        int curr,
        int pos,
        List<Integer> patterns
    ) {
        if (pos == m) {
            patterns.add(curr);
            return;
        }
        for (int i = 0; i < 3; i++) {
            if (pos == 0 || (curr % 3) != i) { // Ensure no adjacent cells have the same colour
                generatePatterns(m, curr * 3 + i, pos + 1, patterns);
            }
        }
    }

    // Helper method to check if two patterns are vertically compatible
    private boolean isCompatible(int p1, int p2, int m) {
        for (int i = 0; i < m; i++) {
            if ((p1 % 3) == (p2 % 3)) { // Conflict if colours are the same
                return false;
            }
            p1 /= 3;
            p2 /= 3;
        }
        return true;
    }
}

Python

class Solution:
    MOD = 10**9 + 7

    def colorTheGrid(self, m: int, n: int) -> int:
        # Generate all valid patterns for one column
        def generate_patterns(pos: int, curr: int) -> List[int]:
            if pos == m:
                patterns.append(curr)
                return
            for c in range(3):
                if pos == 0 or c != curr % 3:
                    generate_patterns(pos + 1, curr * 3 + c)

        def is_compatible(p1: int, p2: int) -> bool:
            for _ in range(m):
                if p1 % 3 == p2 % 3:
                    return False
                p1 //= 3
                p2 //= 3
            return True

        # Precompute valid column patterns and compatibility
        patterns: List[int] = []
        generate_patterns(0, 0)
        k = len(patterns)

        compatibility = [[is_compatible(p1, p2) for p2 in patterns] for p1 in patterns]

        # Initialize DP, one column at a time
        dp: List[int] = [1] * k
        
        for _ in range(1, n):
            new_dp = [0] * k
            for i in range(k):
                for j in range(k):
                    if compatibility[i][j]:
                        new_dp[i] = (new_dp[i] + dp[j]) % self.MOD
            dp = new_dp

        # Return total count
        return sum(dp) % self.MOD

Complexity

• ⏰ Time complexity: O((3^m) * (3^m) * n)
  • Computing all valid row patterns (for m) takes 3^m time.
  • The DP solution iterates over valid row patterns, hence overall time complexity is O((3^m) * (3^m) * n).
• 🧺 Space complexity: O(3^m)
  • Storing valid row patterns requires O(3^m).
  • The DP table requires another O(3^m).
  • Thus, total space complexity is O(3^m).