Palindrome Partitioning

Problem

Given a string s, partition s such that every substring of the partition is a palindrome. Return all possible palindrome partitioning of s.

Definition

[Palindrome Definition](/gk/algorithms/palindrome-definition)

Examples

Example 1:

Input: s = "aab"
Output:[["a","a","b"],["aa","b"]]

Example 2:

Input: s = "a"
Output:[["a"]]

Solution

Method 1 - Depth-first Search and Backtracking

In the examples, we can see each char itself is palindrome. For aab, we have a, a and b. But then we have to break aab again to aa and b. This is how the decision tree looks:

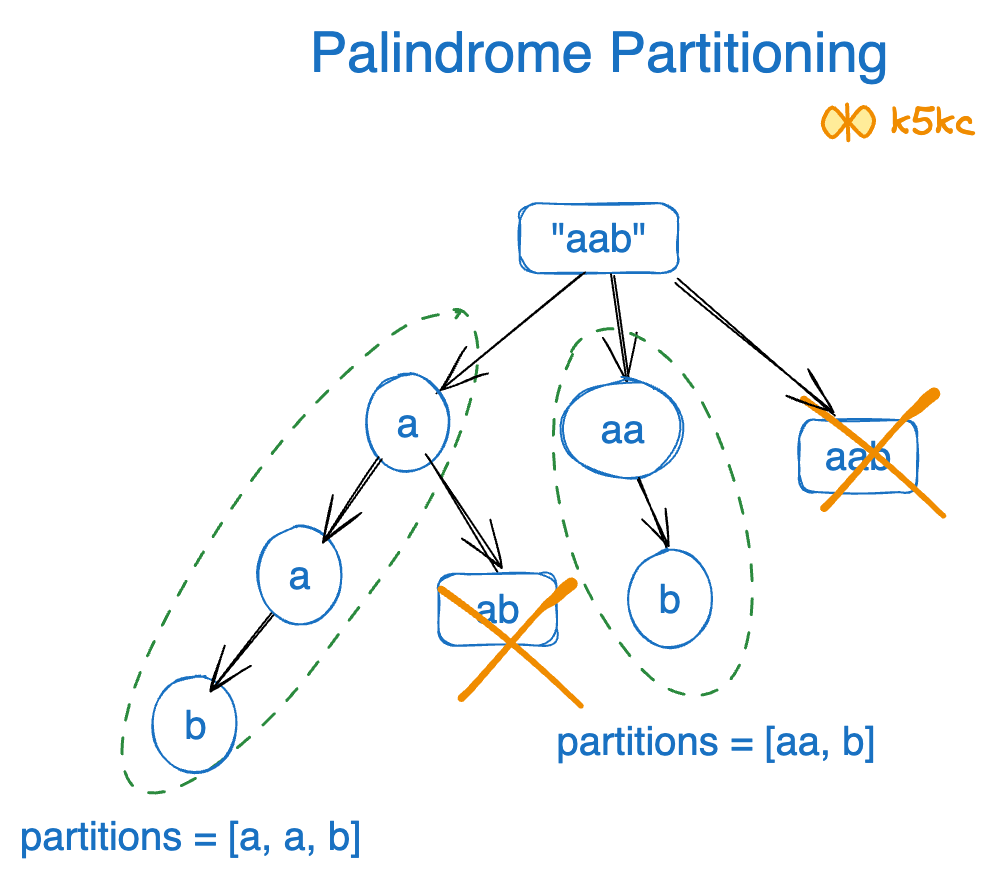
We have already seen how to [Check if given string is palindrome or not](check-if-given-string-is-palindrome-or-not).

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/kTOFIMN16FY" frameborder="0" allowfullscreen></iframe></div>

Code

Java

subAns tracks the current partition.

Without Caching isPalindrome

class Solution {
    public List < List<String>> partition(String s) {
        List < List<String>> ans = new ArrayList<>();

        if (s == null || s.length() == 0) {
            return ans;
        }

        //track each possible partition
        dfs(s, 0, new ArrayList<String>(), ans);

        return ans;
    }


    private void dfs(String s, int idx, List<String> subAns, List < List<String>> ans) {
        //stop condition
        if (idx == s.length()) {
            ans.add(new ArrayList<String> (subAns));
            return;
        }

        for (int i = idx; i < s.length(); i++) {
            String str = s.substring(idx, i + 1);

            if (isPalindrome(str)) {
                subAns.add(str); // take the substr and store it in subAns & call the next substr from idx + 1
                dfs(s, i + 1, subAns, ans);
                subAns.remove(subAns.size() - 1); // remove the string, and try now with substr(idx, i + 2) for eg.
            }
        }
    }


    private boolean isPalindrome(String str) {
        int left = 0;
        int right = str.length() - 1;

        while (left < right) {
            if (str.charAt(left) != str.charAt(right)) {
                return false;
            }

            left++;
            right--;
        }

        return true;
    }
}

Caching isPalindrome

We can make algorithm faster, by caching isPalindrome function using map of string and isPalindrome.

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> ans = new ArrayList<>();

        if (s == null || s.length() == 0) {
            return ans;
        }

        dfs(s, 0, new ArrayList<String>(), ans, new HashMap<>());

        return ans;
    }

    private void dfs(String s, int idx, List<String> subAns, List<List<String>> ans, Map<String, Boolean> map) {
        //stop condition
        if (idx == s.length()) {
            ans.add(new ArrayList<String>(subAns));
            return;
        }

        for (int i = idx; i < s.length(); i++) {
            String str = s.substring(idx, i + 1);
            if (isPalindrome(str, map)) {
                subAns.add(str);
                dfs(s, i + 1, subAns, ans, map);
                subAns.remove(subAns.size() - 1);
            }
        }
    }

    private boolean isPalindrome(String str, Map<String, Boolean> map) {
        if (map.containsKey(str)) {
            return map.get(str);
        }
        boolean isPal = isPalindrome(str);
        map.put(str, isPal);
        return isPal;
    }

    private boolean isPalindrome(String str) {
        int left = 0;
        int right = str.length() - 1;

        while (left<right) {
            if (str.charAt(left) != str.charAt(right)) {
                return false;
            }

            left++;
            right--;
        }

        return true;
    }
}

Complexity

• ⏰ Time complexity: O(n.2^n)
• 🧺 Space complexity: O(n) (using recursion stack)