Problem

Given a string s, return the number of palindromic substrings in it.

A string is a palindrome when it reads the same backward as forward.

A substring is a contiguous sequence of characters within the string.

Examples

Example 1:

Input: s = "abc"
Output: 3

Explanation: Three palindromic strings: “a”, “b”, “c”.

Example 2:

Input: s = "aaa"
Output: 6

Explanation: Six palindromic strings: “a”, “a”, “a”, “aa”, “aa”, “aaa”.

Solution

Method 1 - Brute Force

Create all substrings, by nested looping and check if the strings are palindrome or note.

Time complexity for generating substring is O(n^2) and checking palindrome is O(n), hence time complexity is O(n^3).

Method 2 - Going Outward on Each Index and Check for Palindrome

We have solved similar problem - Longest Palindromic Substring.

For each char, we will go 1 to left and 1 to right, if the chars match, that is 1 substring:

For eg. s[1] is palindrome, as it is just 1 char. Now, we go left or right. As, s[0] and s[2] are same chars, s[0:2] is now a palindrome as well. But this approach gives us odd length palindrome.

To, get even length palindrome, we have to take 2 chars, with left pointer being L and Right pointer being L+1.

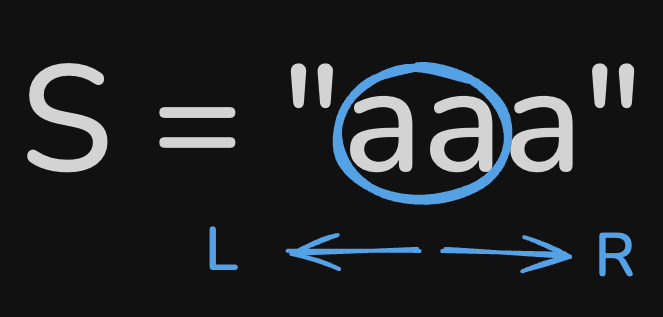
Code

Java
class Solution {
	public int countSubstrings(String s) {
		int ans = 0;
		int n = s.length();
		char[] arr = s.toCharArray();
		int l,r;
	    l = r = 0;
		for (int i = 0; i < n; i++) {
			// odd length
			l = r = i;
			while(l >= 0 && r < n && arr[l]==arr[r]){
				ans += 1;
				l--;
				r++;
			}
			
			// even length
			l = i;
			r = i + 1;
			while(l >= 0 && r < n && arr[l]==arr[r]){
				ans += 1;
				l--;
				r++;
			}
		}
		return ans;
	}
}
Python
class Solution:
    def countSubstrings(self, s: str) -> int:
        ans = 0
        n = len(s)
        arr = list(s)
        
        for i in range(n):
            # Odd length
            l = r = i
            while l >= 0 and r < n and arr[l] == arr[r]:
                ans += 1
                l -= 1
                r += 1
            
            # Even length
            l = i
            r = i + 1
            while l >= 0 and r < n and arr[l] == arr[r]:
                ans += 1
                l -= 1
                r += 1
    
        return ans

Complexity

  • ⏰ Time complexity: O(n^2) for nested loops.
  • 🧺 Space complexity: O(n) for storing results.

Method 3 - Using DP

Here is the approach:

  1. DP Table:
    • dp[i][j] is True if the substring s[i:j+1] is a palindrome.
    • Otherwise, dp[i][j] is False.
  2. Base Cases:
    • Substrings of length 1 (i == j) are always palindromes, so we initialise dp[i][i] = True.
    • Substrings of length 2 (s[i] == s[i+1]) are palindromes if both characters are the same.
  3. General Case:
    • For substrings of length 3 or more, s[i:j+1] is a palindrome if:
      • The first and last characters are the same: s[i] == s[j].
      • The substring in between (s[i+1:j]) is also a palindrome: dp[i+1][j-1] = True.

Code

Java
public int countSubstrings(String s) {
    int n = s.length();
    boolean[][] dp = new boolean[n][n]; // DP table to track palindromic substrings
    int count = 0;

    // Base case: Single character substrings are always palindromes
    for (int i = 0; i < n; i++) {
        dp[i][i] = true;
        count++;
    }

    // Base case: Two consecutive characters are palindromes if they are the same
    for (int i = 0; i < n - 1; i++) {
        if (s.charAt(i) == s.charAt(i + 1)) {
            dp[i][i + 1] = true;
            count++;
        }
    }

    // General case: Substrings of length >= 3
    for (int length = 3; length <= n; length++) { // length goes from 3 to n
        for (int i = 0; i <= n - length; i++) {  // Starting index of the substring
            int j = i + length - 1;  // Ending index of the substring

            // A substring is a palindrome if its first and last characters match,
            // and the substring without them is also a palindrome
            if (s.charAt(i) == s.charAt(j) && dp[i + 1][j - 1]) {
                dp[i][j] = true;
                count++;
            }
        }
    }

    return count;
}
Python
def countSubstrings(s: str) -> int:
    n = len(s)
    dp = [[False] * n for _ in range(n)]  # DP table to track palindromic substrings
    count = 0

    # Base case: Single character substrings are always palindromes
    for i in range(n):
        dp[i][i] = True
        count += 1

    # Base case: Two consecutive characters are palindromes if they are the same
    for i in range(n - 1):
        if s[i] == s[i + 1]:
            dp[i][i + 1] = True
            count += 1

    # General case: Substrings of length >= 3
    for length in range(3, n + 1):  # length goes from 3 to n
        for i in range(n - length + 1):  # Starting index of the substring
            j = i + length - 1  # Ending index of the substring

            # A substring is a palindrome if its first and last characters match,
            # and the substring without them is also a palindrome
            if s[i] == s[j] and dp[i + 1][j - 1]:
                dp[i][j] = True
                count += 1

    return count

Complexity

  • ⏰ Time complexity: O(n^2), since it iterates over each substring (nested loops).
  • 🧺 Space complexity: O(n^2) for using dp array.