Problem

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given an array relations where relations[i] = [prevCoursei, nextCoursei], representing a prerequisite relationship between course prevCoursei and course nextCoursei: course prevCoursei has to be taken before course nextCoursei.

In one semester, you can take any number of courses as long as you have taken all the prerequisites in the previous semester for the courses you are taking.

Return theminimum number of semesters needed to take all courses. If there is no way to take all the courses, return -1.

Examples

Example 1:

1
2
3
4
5
6

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1100-1199/1136.Parallel%20Courses/images/course1graph.jpg)
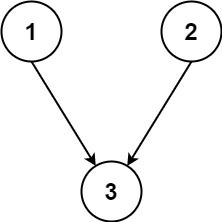
Input: n = 3, relations = [[1,3],[2,3]]
Output: 2
Explanation: The figure above represents the given graph.
In the first semester, you can take courses 1 and 2.
In the second semester, you can take course 3.

Example 2:

1
2
3
4

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1100-1199/1136.Parallel%20Courses/images/course2graph.jpg)
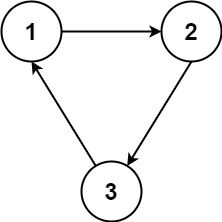
Input: n = 3, relations = [[1,2],[2,3],[3,1]]
Output: -1
Explanation: No course can be studied because they are prerequisites of each other.

Constraints:

  • 1 <= n <= 5000
  • 1 <= relations.length <= 5000
  • relations[i].length == 2
  • 1 <= prevCoursei, nextCoursei <= n
  • prevCoursei != nextCoursei
  • All the pairs [prevCoursei, nextCoursei] are unique.

Solution

Method 1 – Topological Sort (Kahn’s Algorithm)

Intuition

We need to find the minimum number of semesters to finish all courses, where in each semester we can take any number of courses as long as all their prerequisites are completed. This is equivalent to finding the longest path in a DAG (Directed Acyclic Graph) formed by the prerequisites. If there is a cycle, it’s impossible to finish all courses.

Approach

  1. Build a graph and compute the in-degree for each course.
  2. Use a queue to perform BFS (Kahn’s algorithm):
    • Start with all courses with in-degree 0 (no prerequisites).
    • For each semester, process all courses in the queue (can be taken in parallel), and reduce the in-degree of their neighbors.
    • Add neighbors with in-degree 0 to the queue for the next semester.
  3. Count the number of semesters (levels of BFS).
  4. If all courses are processed, return the number of semesters; otherwise, return -1 (cycle detected).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
public:
    int minimumSemesters(int n, vector<vector<int>>& relations) {
        vector<vector<int>> g(n+1);
        vector<int> indeg(n+1, 0);
        for (auto& r : relations) {
            g[r[0]].push_back(r[1]);
            indeg[r[1]]++;
        }
        queue<int> q;
        for (int i = 1; i <= n; ++i) if (indeg[i] == 0) q.push(i);
        int taken = 0, sem = 0;
        while (!q.empty()) {
            int sz = q.size();
            for (int i = 0; i < sz; ++i) {
                int u = q.front(); q.pop();
                taken++;
                for (int v : g[u]) {
                    if (--indeg[v] == 0) q.push(v);
                }
            }
            sem++;
        }
        return taken == n ? sem : -1;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

func minimumSemesters(n int, relations [][]int) int {
    g := make([][]int, n+1)
    indeg := make([]int, n+1)
    for _, r := range relations {
        g[r[0]] = append(g[r[0]], r[1])
        indeg[r[1]]++
    }
    q := []int{}
    for i := 1; i <= n; i++ {
        if indeg[i] == 0 {
            q = append(q, i)
        }
    }
    taken, sem := 0, 0
    for len(q) > 0 {
        sz := len(q)
        next := []int{}
        for i := 0; i < sz; i++ {
            u := q[i]
            taken++
            for _, v := range g[u] {
                indeg[v]--
                if indeg[v] == 0 {
                    next = append(next, v)
                }
            }
        }
        q = next
        sem++
    }
    if taken == n {
        return sem
    }
    return -1
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    public int minimumSemesters(int n, int[][] relations) {
        List<List<Integer>> g = new ArrayList<>();
        for (int i = 0; i <= n; i++) g.add(new ArrayList<>());
        int[] indeg = new int[n+1];
        for (int[] r : relations) {
            g.get(r[0]).add(r[1]);
            indeg[r[1]]++;
        }
        Queue<Integer> q = new LinkedList<>();
        for (int i = 1; i <= n; i++) if (indeg[i] == 0) q.offer(i);
        int taken = 0, sem = 0;
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int u = q.poll();
                taken++;
                for (int v : g.get(u)) {
                    if (--indeg[v] == 0) q.offer(v);
                }
            }
            sem++;
        }
        return taken == n ? sem : -1;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    fun minimumSemesters(n: Int, relations: Array<IntArray>): Int {
        val g = Array(n+1) { mutableListOf<Int>() }
        val indeg = IntArray(n+1)
        for (r in relations) {
            g[r[0]].add(r[1])
            indeg[r[1]]++
        }
        var taken = 0
        var sem = 0
        var q = mutableListOf<Int>()
        for (i in 1..n) if (indeg[i] == 0) q.add(i)
        while (q.isNotEmpty()) {
            val next = mutableListOf<Int>()
            for (u in q) {
                taken++
                for (v in g[u]) {
                    indeg[v]--
                    if (indeg[v] == 0) next.add(v)
                }
            }
            q = next
            sem++
        }
        return if (taken == n) sem else -1
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution:
    def minimumSemesters(self, n: int, relations: list[list[int]]) -> int:
        g = [[] for _ in range(n+1)]
        indeg = [0] * (n+1)
        for u, v in relations:
            g[u].append(v)
            indeg[v] += 1
        q = [i for i in range(1, n+1) if indeg[i] == 0]
        taken = sem = 0
        while q:
            nxt = []
            for u in q:
                taken += 1
                for v in g[u]:
                    indeg[v] -= 1
                    if indeg[v] == 0:
                        nxt.append(v)
            q = nxt
            sem += 1
        return sem if taken == n else -1
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

impl Solution {
    pub fn minimum_semesters(n: i32, relations: Vec<Vec<i32>>) -> i32 {
        let n = n as usize;
        let mut g = vec![vec![]; n+1];
        let mut indeg = vec![0; n+1];
        for r in relations.iter() {
            g[r[0] as usize].push(r[1] as usize);
            indeg[r[1] as usize] += 1;
        }
        let mut q: Vec<usize> = (1..=n).filter(|&i| indeg[i] == 0).collect();
        let mut taken = 0;
        let mut sem = 0;
        while !q.is_empty() {
            let mut next = vec![];
            for &u in &q {
                taken += 1;
                for &v in &g[u] {
                    indeg[v] -= 1;
                    if indeg[v] == 0 {
                        next.push(v);
                    }
                }
            }
            q = next;
            sem += 1;
        }
        if taken == n { sem } else { -1 }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    minimumSemesters(n: number, relations: number[][]): number {
        const g: number[][] = Array.from({length: n+1}, () => []);
        const indeg: number[] = Array(n+1).fill(0);
        for (const [u, v] of relations) {
            g[u].push(v);
            indeg[v]++;
        }
        let taken = 0, sem = 0;
        let q: number[] = [];
        for (let i = 1; i <= n; i++) if (indeg[i] === 0) q.push(i);
        while (q.length) {
            const next: number[] = [];
            for (const u of q) {
                taken++;
                for (const v of g[u]) {
                    indeg[v]--;
                    if (indeg[v] === 0) next.push(v);
                }
            }
            q = next;
            sem++;
        }
        return taken === n ? sem : -1;
    }
}

Complexity

  • ⏰ Time complexity: O(n + m), where n is the number of courses and m is the number of relations. Each edge and node is processed once.
  • 🧺 Space complexity: O(n + m), for the adjacency list and in-degree array.