Problem

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.

You must find the minimum number of months needed to complete all the courses following these rules:

  • You may start taking a course at any time if the prerequisites are met.
  • Any number of courses can be taken at the same time.

Return the minimum number of months needed to complete all the courses.

Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).

Examples

Example 1:

1
2
3
4
5
6
7
8

Input:
n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
Output:
 8
Explanation: The figure above represents the given graph and the time required to complete each course.
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

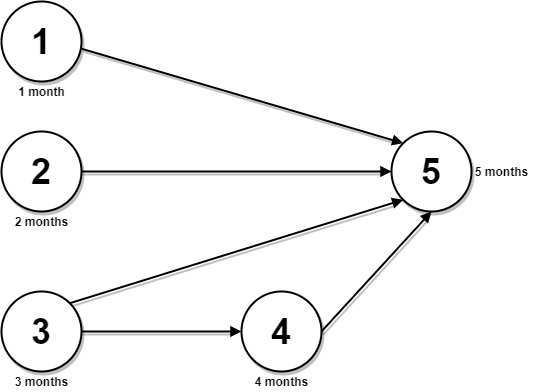
Input:
n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
Output:
 12
Explanation: The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.

Solution

Method 1 – Topological Sort with Dynamic Programming (1)

Intuition

The key idea is to use topological sorting to process courses in order of their dependencies. For each course, the minimum time to finish it is the maximum time to finish all its prerequisites plus its own time. This can be efficiently computed using dynamic programming as we traverse the graph in topological order.

Approach

  1. Build the graph and compute the in-degree for each course.
  2. Initialize a queue with all courses having in-degree zero (no prerequisites).
  3. For each course taken from the queue:
    • For each neighbor (dependent course), update its earliest finish time as the maximum of its current value and the finish time of the current course plus its own time.
    • Decrement the in-degree of the neighbor. If it becomes zero, add it to the queue.
  4. The answer is the maximum finish time among all courses.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int minimumTime(int n, vector<vector<int>>& relations, vector<int>& time) {
        vector<vector<int>> g(n);
        vector<int> indeg(n), dp(time);
        for (auto& e : relations) {
            g[e[0]-1].push_back(e[1]-1);
            indeg[e[1]-1]++;
        }
        queue<int> q;
        for (int i = 0; i < n; ++i) if (indeg[i] == 0) q.push(i);
        while (!q.empty()) {
            int u = q.front(); q.pop();
            for (int v : g[u]) {
                if (dp[v] < dp[u] + time[v]) dp[v] = dp[u] + time[v];
                if (--indeg[v] == 0) q.push(v);
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

func minimumTime(n int, relations [][]int, time []int) int {
    g := make([][]int, n)
    indeg := make([]int, n)
    dp := make([]int, n)
    copy(dp, time)
    for _, e := range relations {
        g[e[0]-1] = append(g[e[0]-1], e[1]-1)
        indeg[e[1]-1]++
    }
    q := []int{}
    for i := 0; i < n; i++ {
        if indeg[i] == 0 {
            q = append(q, i)
        }
    }
    for len(q) > 0 {
        u := q[0]
        q = q[1:]
        for _, v := range g[u] {
            if dp[v] < dp[u]+time[v] {
                dp[v] = dp[u] + time[v]
            }
            indeg[v]--
            if indeg[v] == 0 {
                q = append(q, v)
            }
        }
    }
    ans := 0
    for _, v := range dp {
        if v > ans {
            ans = v
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
    public int minimumTime(int n, int[][] relations, int[] time) {
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; i++) g[i] = new ArrayList<>();
        int[] indeg = new int[n], dp = time.clone();
        for (int[] e : relations) {
            g[e[0]-1].add(e[1]-1);
            indeg[e[1]-1]++;
        }
        Queue<Integer> q = new ArrayDeque<>();
        for (int i = 0; i < n; i++) if (indeg[i] == 0) q.add(i);
        while (!q.isEmpty()) {
            int u = q.poll();
            for (int v : g[u]) {
                if (dp[v] < dp[u] + time[v]) dp[v] = dp[u] + time[v];
                if (--indeg[v] == 0) q.add(v);
            }
        }
        int ans = 0;
        for (int v : dp) ans = Math.max(ans, v);
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    fun minimumTime(n: Int, relations: Array<IntArray>, time: IntArray): Int {
        val g = Array(n) { mutableListOf<Int>() }
        val indeg = IntArray(n)
        val dp = time.copyOf()
        for (e in relations) {
            g[e[0]-1].add(e[1]-1)
            indeg[e[1]-1]++
        }
        val q = ArrayDeque<Int>()
        for (i in 0 until n) if (indeg[i] == 0) q.add(i)
        while (q.isNotEmpty()) {
            val u = q.removeFirst()
            for (v in g[u]) {
                if (dp[v] < dp[u] + time[v]) dp[v] = dp[u] + time[v]
                if (--indeg[v] == 0) q.add(v)
            }
        }
        return dp.maxOrNull() ?: 0
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

class Solution:
    def minimumTime(self, n: int, relations: list[list[int]], time: list[int]) -> int:
        g = [[] for _ in range(n)]
        indeg = [0] * n
        dp = time[:]
        for u, v in relations:
            g[u-1].append(v-1)
            indeg[v-1] += 1
        q = [i for i in range(n) if indeg[i] == 0]
        while q:
            u = q.pop(0)
            for v in g[u]:
                if dp[v] < dp[u] + time[v]:
                    dp[v] = dp[u] + time[v]
                indeg[v] -= 1
                if indeg[v] == 0:
                    q.append(v)
        return max(dp)
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

impl Solution {
    pub fn minimum_time(n: i32, relations: Vec<Vec<i32>>, time: Vec<i32>) -> i32 {
        let n = n as usize;
        let mut g = vec![vec![]; n];
        let mut indeg = vec![0; n];
        let mut dp = time.clone();
        for e in relations.iter() {
            g[(e[0]-1) as usize].push((e[1]-1) as usize);
            indeg[(e[1]-1) as usize] += 1;
        }
        let mut q = vec![];
        for i in 0..n {
            if indeg[i] == 0 {
                q.push(i);
            }
        }
        while let Some(u) = q.get(0).cloned() {
            q.remove(0);
            for &v in &g[u] {
                if dp[v] < dp[u] + time[v] {
                    dp[v] = dp[u] + time[v];
                }
                indeg[v] -= 1;
                if indeg[v] == 0 {
                    q.push(v);
                }
            }
        }
        *dp.iter().max().unwrap()
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    minimumTime(n: number, relations: number[][], time: number[]): number {
        const g: number[][] = Array.from({length: n}, () => []);
        const indeg = Array(n).fill(0);
        const dp = time.slice();
        for (const [u, v] of relations) {
            g[u-1].push(v-1);
            indeg[v-1]++;
        }
        const q: number[] = [];
        for (let i = 0; i < n; i++) if (indeg[i] === 0) q.push(i);
        while (q.length) {
            const u = q.shift()!;
            for (const v of g[u]) {
                if (dp[v] < dp[u] + time[v]) dp[v] = dp[u] + time[v];
                if (--indeg[v] === 0) q.push(v);
            }
        }
        return Math.max(...dp);
    }
}

Complexity

  • ⏰ Time complexity: O(n + m), where n is the number of courses and m is the number of relations; each node and edge is processed once.
  • 🧺 Space complexity: O(n + m), for the graph, in-degree array, and dp array.