Problem

Given an integer numRows, return the first numRows of Pascal’s triangle.

Examples

Example 1:

1
2

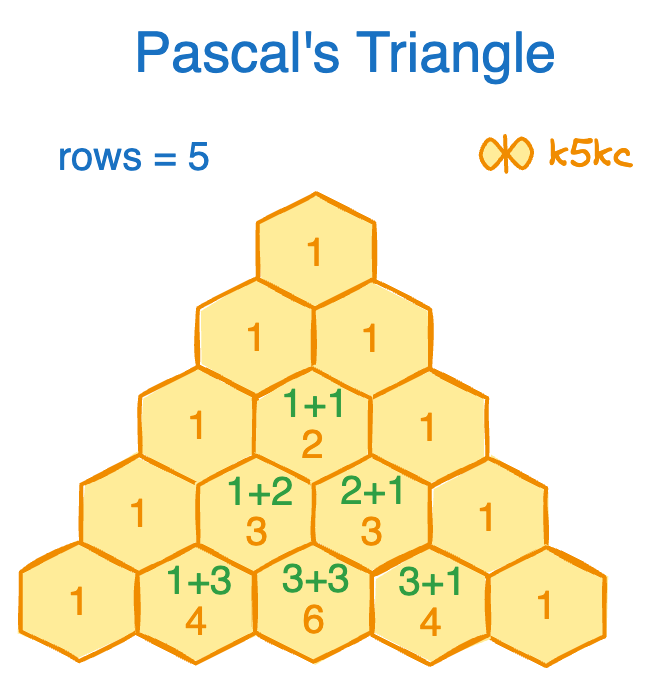
Input: numRows = 5
Output:[[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

This is how the pascal triangle will look:

1
2
3
4
5
6
7

[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

Example 2:

1
2

Input: numRows = 1
Output:[[1]]

For example, given numRows = 5, the result should be:

Follow up

Can you do this using only O(n) space? where n is number of rows.

Solution

Method 1 - Recursion

Here is how the recursion work:

  • Base case: If numRows is 1, return [[1]].
  • Recursively generate the triangle for numRows - 1.
  • Calculate the current row by summing adjacent elements from the previous row.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    public List<List<Integer>> generate(int numRows) {
        if (numRows == 0) {
	        return new ArrayList<>();
	    }
        if (numRows == 1) {
		    List<List<Integer>> ans = new ArrayList<>();
			ans.add(new ArrayList<>(List.of(1)));
            return ans;
        }
        
        List<List<Integer>> prevRows = generate(numRows - 1);
        List<Integer> newRow = new ArrayList<>();
        
        for (int i = 0; i < numRows; i++) {
            newRow.add(1);
        }
        
        for (int i = 1; i < numRows - 1; i++) {
            newRow.set(i, prevRows.get(numRows - 2).get(i - 1) + prevRows.get(numRows - 2).get(i));
        }
        
        prevRows.add(newRow);
        return prevRows;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2). generate is called for numRows times, and in that we have loop to fill newRow from old row, and that takes O(n) time. So, time complexity is O(n^2).
  • 🧺 Space complexity: O(n) for the recursive stack.

Method 2 - Generating binomial coeff in each row

We can use Binomial Coefficient. We know that formula is: $$ C(n, k) = \frac{n!}{k! * (n - k)!} $$

We can fill the values in nth row and kth column. For eg.

  • row 1 ⇨ n = 0, k = 0 and C(0, 0,) = 1
  • row 2 ⇨ n = 1. k is in range [0, 1]. C(1, 0) = 1!/0!1! = 1, C(1, 1) = 1
  • and so on.

So, for nth row, and kth column we will use C(n - 1, k - 1) to fill it up.

To sum it up:

  • Use the binomial coefficient formula C(n, k) to calculate each element.
  • Build the triangle row by row using the formula.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Solution {

	public List < List<Integer>> generate(int numRows) {
		List < List<Integer>> ans = new ArrayList<>();

		for (int row = 1; row <= numRows; row++) {
			List<Integer> currRow = new ArrayList<>();

			for (int col = 1; col <= row; col++) {
				currRow.add(binomialCoeff(row - 1, col - 1));
			}

			ans.add(currRow);
		}

		return ans;
	}

	private int binomialCoeff(int n, int k) {
		int ans = 1;

		if (k > n - k) {
			k = n - k;
		}

		for (int i = 0; i < k; ++i) {
			ans *= (n - i);
			ans /= (i + 1);
		}

		return ans;
	}
}

Complexity

  • ⏰ Time complexity: O(n^3) - O(n^2) for nested loop in generate, and then O(n) time for generating the binomial coefficient.
  • 🧺 Space complexity: O(1)

Method 3 - Reuse the generated binomial coefficient

This is optimization on previous solution. Once, we calculate the value for nth row, and kth column, we can use it to generate the values.

If we take a closer at the triangle, we observe that every entry is sum of the two values above it.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {

	public List < List<Integer>> generate(int numRows) {
		List <List<Integer>> ans = new ArrayList<>();
		// do the first row separately to avoid if condition on prevRow in loop
        List<Integer> firstRow = new ArrayList<>();
        firstRow.add(1);
        ans.add(firstRow);
		// note: no row<= numRows, as first row already handled
		for (int row = 1; row < numRows; row++) {
			List<Integer> prevRow = ans.get(row - 1);
			List<Integer> currRow = new ArrayList<>();
            
            currRow.add(1);
            // no col <= row here as well, to handle index out of bounds
			for (int col = 1; col < row; col++) {
				currRow.add(prevRow.get(col - 1) + prevRow.get(col));
			}
            currRow.add(1);
            
			ans.add(currRow);
		}

		return ans;
	}
}

Complexity

  • ⏰ Time complexity: O(n^2)
  • 🧺 Space complexity: O(1) (as we return the answer, no aux space is used, but O(n) space)