Pascal’s Triangle 2 - Return nth row

Problem

Given an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.

In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:

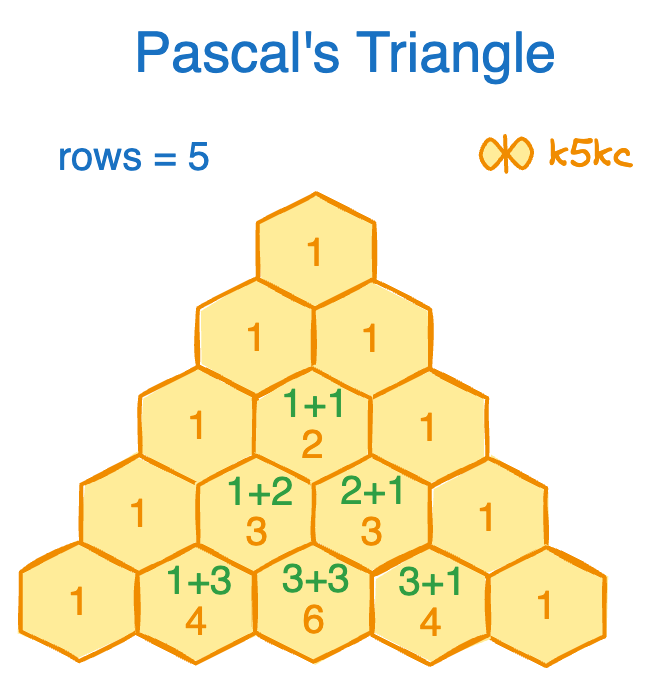
OR

Given an input k, return the kth row of Pascal's triangle.

Bonus: Can you do this using only O(k) space?

Examples

Example 1:

Input: rowIndex = 3
Output: [1,3,3,1]

Example 2:

Input: rowIndex = 0
Output: [1]

Example 3:

Input: rowIndex = 1
Output: [1,1]

Solution

Method 1 - Use the generate function

This problem is related to [Pascal's Triangle](pascal-s-triangle-1-generate-first-n-rows) which gets all rows of Pascal's triangle. In this problem, only one row is required to return. So, we can generate the whole triangle and return the last row.

class Solution {
	public List<Integer> getRow(int rowIndex) {
		List<List<Integer>> allRows = generate(rowIndex);
		return allRows.get(rowIndex);
	}
}

Method 2 - Simple Iteration

We can use method similar to method 3.

Code

Java

public class Solution {

	public List<Integer> getRow(int rowIndex) {
		List<Integer> row = new ArrayList<>(rowIndex + 1);

		for (int i = 0; i < rowIndex + 1; i++) {
			row.add(1);
		}

		// Build the Pascal's triangle row by row
		for (int i = 1; i < rowIndex; i++) {
			for (int j = i; j > 0; j--) {
				row.set(j, row.get(j) + row.get(j - 1));
			}
		}

		return row;
	}
}

Complexity

• ⏰ Time complexity: O(n^2), where n is rowIndex.
• 🧺 Space complexity: O(1)