Problem

You are given an integer n representing the number of nodes in a graph, labeled from 0 to n - 1.

You are also given an integer array nums of length n sorted in non-decreasing order, and an integer maxDiff.

An undirected edge exists between nodes i and j if the absolute difference between nums[i] and nums[j] is at most maxDiff (i.e., |nums[i] - nums[j]| <= maxDiff).

You are also given a 2D integer array queries. For each queries[i] = [ui, vi], determine whether there exists a path between nodes ui and vi.

Return a boolean array answer, where answer[i] is true if there exists a path between ui and vi in the ith query and false otherwise.

Example 1

1
2
3
4
5
6

Input: n = 2, nums = [1,3], maxDiff = 1, queries = [[0,0],[0,1]]
Output: [true,false]
Explanation:
* Query `[0,0]`: Node 0 has a trivial path to itself.
* Query `[0,1]`: There is no edge between Node 0 and Node 1 because `|nums[0] - nums[1]| = |1 - 3| = 2`, which is greater than `maxDiff`.
* Thus, the final answer after processing all the queries is `[true, false]`.

Example 2

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Input: n = 4, nums = [2,5,6,8], maxDiff = 2, queries =
[[0,1],[0,2],[1,3],[2,3]]
Output: [false,false,true,true]
Explanation:
The resulting graph is:
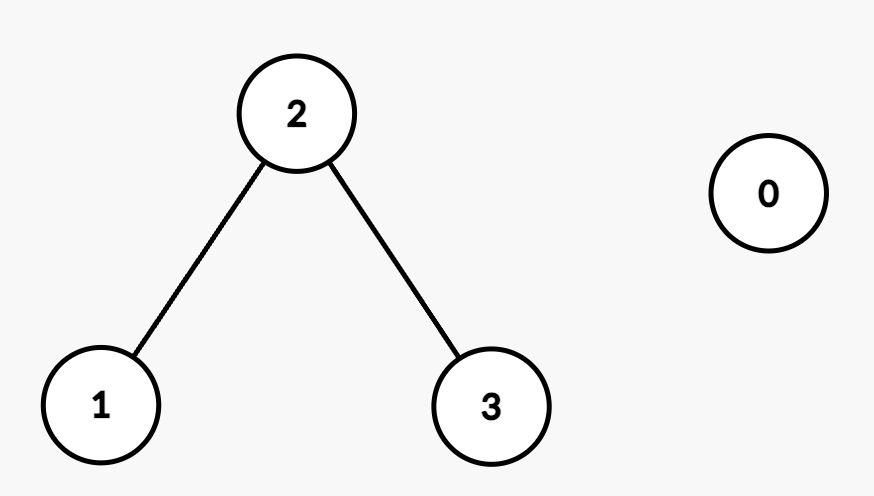
![](https://assets.leetcode.com/uploads/2025/03/25/screenshot-2025-03-26-at-122249.png)
* Query `[0,1]`: There is no edge between Node 0 and Node 1 because `|nums[0] - nums[1]| = |2 - 5| = 3`, which is greater than `maxDiff`.
* Query `[0,2]`: There is no edge between Node 0 and Node 2 because `|nums[0] - nums[2]| = |2 - 6| = 4`, which is greater than `maxDiff`.
* Query `[1,3]`: There is a path between Node 1 and Node 3 through Node 2 since `|nums[1] - nums[2]| = |5 - 6| = 1` and `|nums[2] - nums[3]| = |6 - 8| = 2`, both of which are within `maxDiff`.
* Query `[2,3]`: There is an edge between Node 2 and Node 3 because `|nums[2] - nums[3]| = |6 - 8| = 2`, which is equal to `maxDiff`.
* Thus, the final answer after processing all the queries is `[false, false, true, true]`.

Constraints

  • 1 <= n == nums.length <= 10^5
  • 0 <= nums[i] <= 10^5
  • nums is sorted in non-decreasing order.
  • 0 <= maxDiff <= 10^5
  • 1 <= queries.length <= 10^5
  • queries[i] == [ui, vi]
  • 0 <= ui, vi < n

Examples

Solution

Method 1 - Union-Find (Disjoint Set Union)

Intuition

Since nums is sorted, nodes with consecutive indices are connected if their values differ by at most maxDiff. Thus, the graph consists of connected components formed by joining consecutive nodes where the difference is within maxDiff. We can use Union-Find to efficiently group nodes into components, then answer each query by checking if ui and vi are in the same component.

Approach

  1. Initialize Union-Find for all nodes.
  2. For each i from 1 to n-1, if nums[i] - nums[i-1] <= maxDiff, union i and i-1.
  3. For each query [ui, vi], check if find(ui) == find(vi).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

#include <vector>
using namespace std;
struct DSU {
    vector<int> p;
    DSU(int n): p(n) { for (int i = 0; i < n; ++i) p[i] = i; }
    int find(int x) { return p[x] == x ? x : p[x] = find(p[x]); }
    void unite(int x, int y) { p[find(x)] = find(y); }
};
vector<bool> pathExistence(int n, vector<int>& nums, int maxDiff, vector<vector<int>>& queries) {
    DSU dsu(n);
    for (int i = 1; i < n; ++i) {
        if (nums[i] - nums[i-1] <= maxDiff) dsu.unite(i, i-1);
    }
    vector<bool> res;
    for (auto& q : queries) res.push_back(dsu.find(q[0]) == dsu.find(q[1]));
    return res;
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

func pathExistence(n int, nums []int, maxDiff int, queries [][]int) []bool {
    parent := make([]int, n)
    for i := range parent { parent[i] = i }
    var find func(int) int
    find = func(x int) int {
        if parent[x] != x { parent[x] = find(parent[x]) }
        return parent[x]
    }
    unite := func(x, y int) { parent[find(x)] = find(y) }
    for i := 1; i < n; i++ {
        if nums[i]-nums[i-1] <= maxDiff { unite(i, i-1) }
    }
    res := make([]bool, len(queries))
    for i, q := range queries {
        res[i] = find(q[0]) == find(q[1])
    }
    return res
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

import java.util.*;
class Solution {
    public List<Boolean> pathExistence(int n, int[] nums, int maxDiff, int[][] queries) {
        int[] parent = new int[n];
        for (int i = 0; i < n; ++i) parent[i] = i;
        for (int i = 1; i < n; ++i) {
            if (nums[i] - nums[i-1] <= maxDiff) union(parent, i, i-1);
        }
        List<Boolean> res = new ArrayList<>();
        for (int[] q : queries) res.add(find(parent, q[0]) == find(parent, q[1]));
        return res;
    }
    private int find(int[] p, int x) { return p[x] == x ? x : (p[x] = find(p, p[x])); }
    private void union(int[] p, int x, int y) { p[find(p, x)] = find(p, y); }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

fun pathExistence(n: Int, nums: IntArray, maxDiff: Int, queries: Array<IntArray>): List<Boolean> {
    val parent = IntArray(n) { it }
    fun find(x: Int): Int {
        if (parent[x] != x) parent[x] = find(parent[x])
        return parent[x]
    }
    fun unite(x: Int, y: Int) { parent[find(x)] = find(y) }
    for (i in 1 until n) {
        if (nums[i] - nums[i-1] <= maxDiff) unite(i, i-1)
    }
    return queries.map { find(it[0]) == find(it[1]) }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

from typing import List
def pathExistence(n: int, nums: List[int], maxDiff: int, queries: List[List[int]]) -> List[bool]:
    parent = list(range(n))
    def find(x):
        if parent[x] != x:
            parent[x] = find(parent[x])
        return parent[x]
    def unite(x, y):
        parent[find(x)] = find(y)
    for i in range(1, n):
        if nums[i] - nums[i-1] <= maxDiff:
            unite(i, i-1)
    return [find(u) == find(v) for u, v in queries]
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

pub fn path_existence(n: usize, nums: Vec<i32>, max_diff: i32, queries: Vec<Vec<usize>>) -> Vec<bool> {
    let mut parent: Vec<usize> = (0..n).collect();
    fn find(p: &mut Vec<usize>, x: usize) -> usize {
        if p[x] != x { p[x] = find(p, p[x]); }
        p[x]
    }
    fn unite(p: &mut Vec<usize>, x: usize, y: usize) {
        let px = find(p, x); let py = find(p, y);
        p[px] = py;
    }
    for i in 1..n {
        if nums[i] - nums[i-1] <= max_diff {
            unite(&mut parent, i, i-1);
        }
    }
    queries.iter().map(|q| find(&mut parent.clone(), q[0]) == find(&mut parent.clone(), q[1])).collect()
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

function pathExistence(n: number, nums: number[], maxDiff: number, queries: number[][]): boolean[] {
    const parent = Array.from({length: n}, (_, i) => i);
    function find(x: number): number {
        if (parent[x] !== x) parent[x] = find(parent[x]);
        return parent[x];
    }
    function unite(x: number, y: number) { parent[find(x)] = find(y); }
    for (let i = 1; i < n; ++i) {
        if (nums[i] - nums[i-1] <= maxDiff) unite(i, i-1);
    }
    return queries.map(([u, v]) => find(u) === find(v));
}

Complexity

  • ⏰ Time complexity: O(n + Q * α(n)) where α is the inverse Ackermann function (almost constant), n is the number of nodes, and Q is the number of queries.
  • 🧺 Space complexity: O(n) for the parent array.