Path Existence Queries in a Graph II
Problem
You are given an integer n representing the number of nodes in a graph, labeled from 0 to n - 1.
You are also given an integer array nums of length n and an integer
maxDiff.
An undirected edge exists between nodes i and j if the absolute difference between nums[i] and nums[j] is at most maxDiff (i.e.,
|nums[i] - nums[j]| <= maxDiff).
You are also given a 2D integer array queries. For each queries[i] = [ui, vi], find the minimum distance between nodes ui and vi. If no path exists between the two nodes, return -1 for that query.
Return an array answer, where answer[i] is the result of the ith query.
Note: The edges between the nodes are unweighted.
Examples
Example 1
Input: n = 5, nums = [1,8,3,4,2], maxDiff = 3, queries = [[0,3],[2,4]]
Output: [1,1]
Explanation:
The resulting graph is:
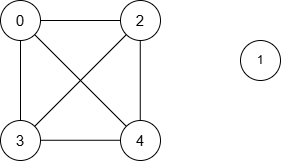
Query | Shortest Path | Minimum Distance
---|---|---
[0, 3] | 0 -> 3 | 1
[2, 4] | 2 -> 4 | 1
Thus, the output is `[1, 1]`.
Example 2
Input: n = 5, nums = [5,3,1,9,10], maxDiff = 2, queries =
[[0,1],[0,2],[2,3],[4,3]]
Output: [1,2,-1,1]
Explanation:
The resulting graph is:
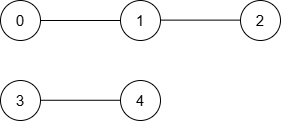
Query | Shortest Path | Minimum Distance
---|---|---
[0, 1] | 0 -> 1 | 1
[0, 2] | 0 -> 1 -> 2 | 2
[2, 3] | None | -1
[4, 3] | 3 -> 4 | 1
Thus, the output is `[1, 2, -1, 1]`.
Example 3
Input: n = 3, nums = [3,6,1], maxDiff = 1, queries = [[0,0],[0,1],[1,2]]
Output: [0,-1,-1]
Explanation:
There are no edges between any two nodes because:
* Nodes 0 and 1: `|nums[0] - nums[1]| = |3 - 6| = 3 > 1`
* Nodes 0 and 2: `|nums[0] - nums[2]| = |3 - 1| = 2 > 1`
* Nodes 1 and 2: `|nums[1] - nums[2]| = |6 - 1| = 5 > 1`
Thus, no node can reach any other node, and the output is `[0, -1, -1]`.
Constraints
1 <= n == nums.length <= 10^50 <= nums[i] <= 10^50 <= maxDiff <= 10^51 <= queries.length <= 10^5queries[i] == [ui, vi]0 <= ui, vi < n
Solution
Method 1 - BFS on-the-fly (Efficient for Sparse Graph)
Intuition
The graph is defined by connecting nodes whose values differ by at most maxDiff. For each query, we need the shortest path between two nodes. Since the graph is implicit and can be very large, we avoid building the full adjacency list. Instead, we use value bucketing and BFS for each query, leveraging the fact that for each node, its neighbors are those with values in [nums[i] - maxDiff, nums[i] + maxDiff].
Approach
- Build a mapping from value to indices (nodes with that value).
- For each query, run BFS from
uitovi, only traversing nodes whose values are withinmaxDiffof the current node. - Use a visited set to avoid cycles.
- If
ui == vi, answer is 0. - If no path exists, return -1.
Code
C++
#include <vector>
#include <queue>
#include <unordered_map>
#include <unordered_set>
using namespace std;
vector<int> minimumDistance(int n, vector<int>& nums, int maxDiff, vector<vector<int>>& queries) {
unordered_map<int, vector<int>> val2idx;
for (int i = 0; i < n; ++i) val2idx[nums[i]].push_back(i);
vector<int> res;
for (auto& q : queries) {
int u = q[0], v = q[1];
if (u == v) { res.push_back(0); continue; }
queue<pair<int, int>> qBFS;
unordered_set<int> visited;
qBFS.push({u, 0});
visited.insert(u);
bool found = false;
while (!qBFS.empty() && !found) {
auto [cur, dist] = qBFS.front(); qBFS.pop();
for (int d = -maxDiff; d <= maxDiff; ++d) {
int val = nums[cur] + d;
if (val2idx.count(val)) {
for (int nei : val2idx[val]) {
if (nei == cur || visited.count(nei)) continue;
if (nei == v) { res.push_back(dist + 1); found = true; break; }
visited.insert(nei);
qBFS.push({nei, dist + 1});
}
}
if (found) break;
}
}
if (!found) res.push_back(-1);
}
return res;
}
Go
func minimumDistance(n int, nums []int, maxDiff int, queries [][]int) []int {
val2idx := map[int][]int{}
for i, v := range nums {
val2idx[v] = append(val2idx[v], i)
}
res := make([]int, 0, len(queries))
for _, q := range queries {
u, v := q[0], q[1]
if u == v {
res = append(res, 0)
continue
}
visited := make(map[int]bool)
queue := [][2]int{{u, 0}}
visited[u] = true
found := false
for len(queue) > 0 && !found {
cur, dist := queue[0][0], queue[0][1]
queue = queue[1:]
for d := -maxDiff; d <= maxDiff; d++ {
val := nums[cur] + d
if idxs, ok := val2idx[val]; ok {
for _, nei := range idxs {
if nei == cur || visited[nei] { continue }
if nei == v {
res = append(res, dist+1)
found = true
break
}
visited[nei] = true
queue = append(queue, [2]int{nei, dist + 1})
}
}
if found { break }
}
}
if !found { res = append(res, -1) }
}
return res
}
Java
import java.util.*;
class Solution {
public List<Integer> minimumDistance(int n, int[] nums, int maxDiff, int[][] queries) {
Map<Integer, List<Integer>> val2idx = new HashMap<>();
for (int i = 0; i < n; ++i) val2idx.computeIfAbsent(nums[i], k -> new ArrayList<>()).add(i);
List<Integer> res = new ArrayList<>();
for (int[] q : queries) {
int u = q[0], v = q[1];
if (u == v) { res.add(0); continue; }
Queue<int[]> qBFS = new LinkedList<>();
Set<Integer> visited = new HashSet<>();
qBFS.offer(new int[]{u, 0});
visited.add(u);
boolean found = false;
while (!qBFS.isEmpty() && !found) {
int[] node = qBFS.poll();
int cur = node[0], dist = node[1];
for (int d = -maxDiff; d <= maxDiff; ++d) {
int val = nums[cur] + d;
if (val2idx.containsKey(val)) {
for (int nei : val2idx.get(val)) {
if (nei == cur || visited.contains(nei)) continue;
if (nei == v) { res.add(dist + 1); found = true; break; }
visited.add(nei);
qBFS.offer(new int[]{nei, dist + 1});
}
}
if (found) break;
}
}
if (!found) res.add(-1);
}
return res;
}
}
Kotlin
fun minimumDistance(n: Int, nums: IntArray, maxDiff: Int, queries: Array<IntArray>): List<Int> {
val val2idx = mutableMapOf<Int, MutableList<Int>>()
for (i in 0 until n) val2idx.getOrPut(nums[i]) { mutableListOf() }.add(i)
val res = mutableListOf<Int>()
for (q in queries) {
val u = q[0]; val v = q[1]
if (u == v) { res.add(0); continue }
val visited = mutableSetOf<Int>()
val queue = ArrayDeque<Pair<Int, Int>>()
queue.add(u to 0)
visited.add(u)
var found = false
while (queue.isNotEmpty() && !found) {
val (cur, dist) = queue.removeFirst()
for (d in -maxDiff..maxDiff) {
val valN = nums[cur] + d
val2idx[valN]?.forEach { nei ->
if (nei == cur || nei in visited) return@forEach
if (nei == v) { res.add(dist + 1); found = true; return@forEach }
visited.add(nei)
queue.add(nei to dist + 1)
}
if (found) break
}
}
if (!found) res.add(-1)
}
return res
}
Python
from collections import defaultdict, deque
from typing import List
def minimumDistance(n: int, nums: List[int], maxDiff: int, queries: List[List[int]]) -> List[int]:
val2idx = defaultdict(list)
for i, v in enumerate(nums):
val2idx[v].append(i)
res = []
for u, v in queries:
if u == v:
res.append(0)
continue
visited = set([u])
q = deque([(u, 0)])
found = False
while q and not found:
cur, dist = q.popleft()
for d in range(-maxDiff, maxDiff + 1):
val = nums[cur] + d
for nei in val2idx.get(val, []):
if nei == cur or nei in visited:
continue
if nei == v:
res.append(dist + 1)
found = True
break
visited.add(nei)
q.append((nei, dist + 1))
if found:
break
if not found:
res.append(-1)
return res
Rust
use std::collections::{HashMap, HashSet, VecDeque};
pub fn minimum_distance(n: i32, nums: Vec<i32>, max_diff: i32, queries: Vec<Vec<i32>>) -> Vec<i32> {
let mut val2idx: HashMap<i32, Vec<usize>> = HashMap::new();
for (i, &v) in nums.iter().enumerate() {
val2idx.entry(v).or_default().push(i);
}
let mut res = Vec::new();
for q in queries.iter() {
let (u, v) = (q[0] as usize, q[1] as usize);
if u == v { res.push(0); continue; }
let mut visited = HashSet::new();
let mut queue = VecDeque::new();
queue.push_back((u, 0));
visited.insert(u);
let mut found = false;
while let Some((cur, dist)) = queue.pop_front() {
for d in -max_diff..=max_diff {
let val = nums[cur] + d;
if let Some(neis) = val2idx.get(&val) {
for &nei in neis {
if nei == cur || visited.contains(&nei) { continue; }
if nei == v { res.push(dist + 1); found = true; break; }
visited.insert(nei);
queue.push_back((nei, dist + 1));
}
}
if found { break; }
}
if found { break; }
}
if !found { res.push(-1); }
}
res
}
TypeScript
function minimumDistance(n: number, nums: number[], maxDiff: number, queries: number[][]): number[] {
const val2idx = new Map<number, number[]>();
for (let i = 0; i < n; ++i) {
if (!val2idx.has(nums[i])) val2idx.set(nums[i], []);
val2idx.get(nums[i])!.push(i);
}
const res: number[] = [];
for (const [u, v] of queries) {
if (u === v) { res.push(0); continue; }
const visited = new Set<number>([u]);
const queue: [number, number][] = [[u, 0]];
let found = false;
while (queue.length && !found) {
const [cur, dist] = queue.shift()!;
for (let d = -maxDiff; d <= maxDiff; ++d) {
const val = nums[cur] + d;
if (val2idx.has(val)) {
for (const nei of val2idx.get(val)!) {
if (nei === cur || visited.has(nei)) continue;
if (nei === v) { res.push(dist + 1); found = true; break; }
visited.add(nei);
queue.push([nei, dist + 1]);
}
}
if (found) break;
}
}
if (!found) res.push(-1);
}
return res;
}
Complexity
- ⏰ Time complexity: For each query, in the worst case,
O(n * maxDiff)(but usually much less if the graph is sparse or maxDiff is small). For all queries:O(Q * n * maxDiff)in the worst case, but typically much faster in practice. - 🧺 Space complexity:
O(n + Q)for value mapping and visited sets.