Problem

Given the root of a binary tree and an integer targetSum, return the number of paths where the sum of the values along the path equals targetSum.

The path does not need to start or end at the root or a leaf, but it must go downwards (i.e., traveling only from parent nodes to child nodes).

Examples

Example 1:

1
2
3
4
5

Input:
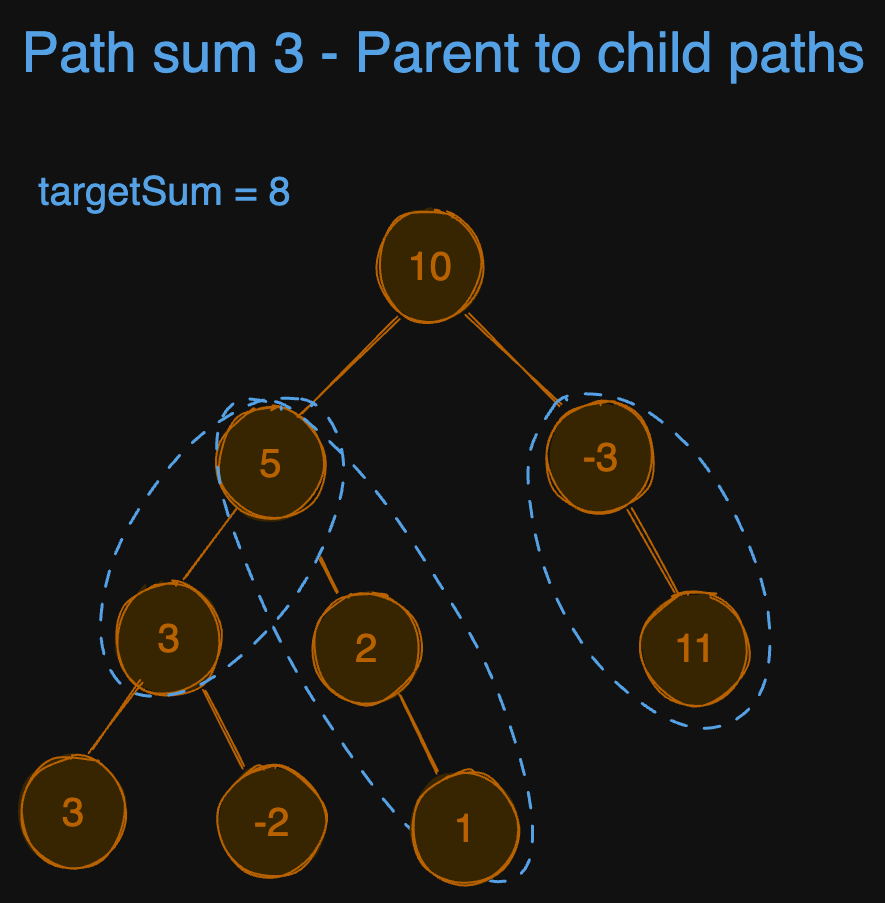
root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
Output:
 3
Explanation: The paths that sum to 8 are shown.

Example 2:

1
2
3
4

Input:
root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
Output:
 3

Solution

Method 1 - Using Prefix sum and hashmap

So the idea is similar as Two Sum, using HashMap to store ( key : the prefix sum, value : how many ways get to this prefix sum).

So, for each node, we check if prefix sum - target exists in hashmap or not, if it does, we added up the ways of prefix sum - target into ans. For instance : in one path we have [1,2,-1,-1,2], then the prefix sum will be: [1, 3, 2, 1, 3], let’s say we want to find target sum is 2, then we will have [[2], [1,2,-1], [2,-1,-1,2] and [2]] aka 4 ways.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    public int pathSum(TreeNode root, int sum) {
        Map<Integer, Integer> map = new HashMap();
        map.put(0,1);
        return helper(root, 0, sum, map);
    }
    
    public int helper(TreeNode root, int currSum, int target, Map<Integer, Integer> map) {
        if (root == null) {
            return 0;
        }
        
        currSum += root.val;
        int ans = map.getOrDefault(currSum - target, 0);
        map.put(currSum, map.getOrDefault(currSum, 0) + 1);
        
        ans += helper(root.left, currSum, target, map) + helper(root.right, currSum, target, map);
        map.put(currSum, map.get(currSum) - 1);
        return ans;
    }
}

Complexity

  • Time: O(n)
  • Space: O(n)

Method 2 - Using DFS

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

public class Solution {
    public int pathSum(TreeNode root, int sum) {
        if (root == null) {
	        return 0;
	    }
        return dfs(root, sum) + pathSum(root.left, sum) + pathSum(root.right, sum);
    }
    
    private int dfs(TreeNode node, int sum) {
        if (node == null) {
	        return 0;
	    }
        return (node.val == sum ? 1 : 0) 
            + dfs(node.left, sum - node.val) + dfs(node.right, sum - node.val);
    }
}

Complexity

  • Time: O(n^2)
  • Space: O(n) due to recursion stack