Path with Maximum Gold

Problem

In a gold mine grid of size m x n, each cell in this mine has an integer representing the amount of gold in that cell, 0 if it is empty.

Return the maximum amount of gold you can collect under the conditions:

• Every time you are located in a cell you will collect all the gold in that cell.
• From your position, you can walk one step to the left, right, up, or down.
• You can't visit the same cell more than once.
• Never visit a cell with 0 gold.
• You can start and stop collecting gold from any position in the grid that has some gold.

Examples

Example 1:

Input: grid =[[0,6,0],[5,8,7],[0,9,0]]
Output: 24
Explanation:
[[0,6,0],
 [5,8,7],
 [0,9,0]]
Path to get the maximum gold, 9 -> 8 -> 7.

Example 2:

Input: grid =[[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
Output: 28
Explanation:
[[1,0,7],
 [2,0,6],
 [3,4,5],
 [0,3,0],
 [9,0,20]]
Path to get the maximum gold, 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7.

Solution

The idea is simple, using backtracking to try all possible paths and return the path with maximum gold. Lets Look at backtracking examples.

Backtracking example

Lets say we start with the node 6, we get sum as 23.

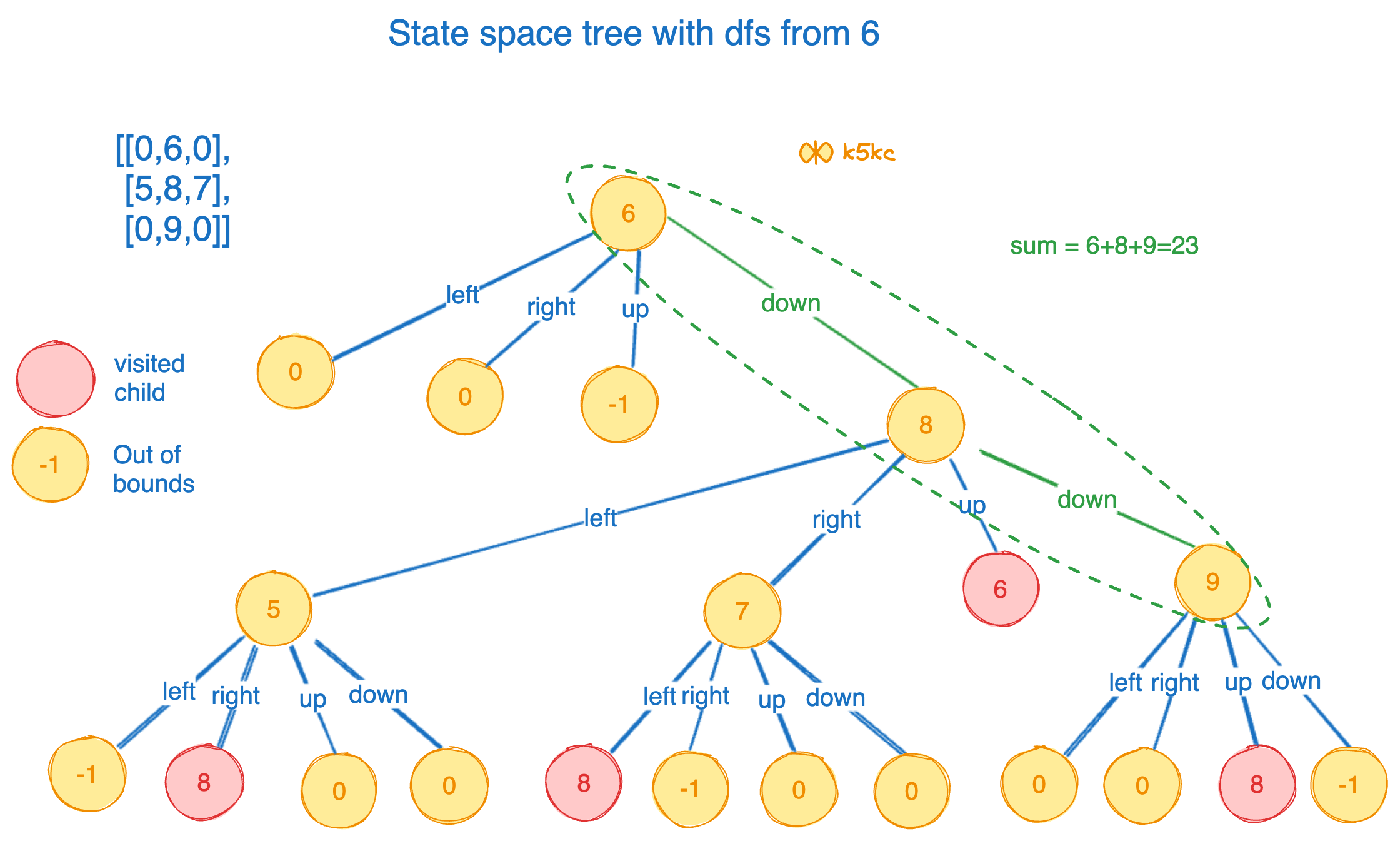
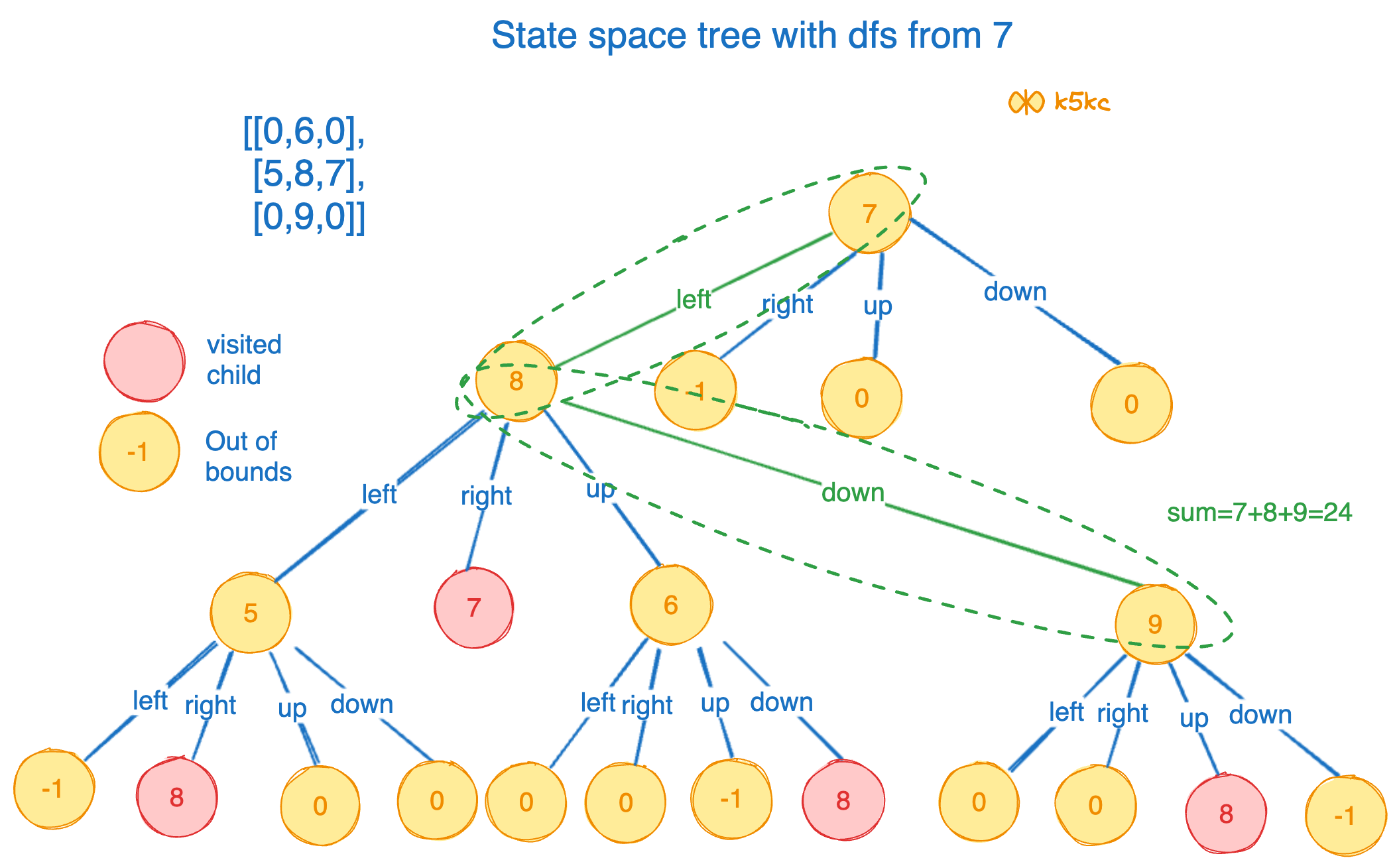
Now, lets look at the case, where we start with the node 7, we get sum as 24, which is what we are expecting:

Why Dynamic Programming (DP) will not work?

One might think that this problem can be solved using DP similar to Leetcode 329 - Longest Increasing Path in a Matrix. Indeed, at face value, it seems we can use a 2D array to store at each position what's the maximum path, which can give us a O(M*N) runtime. However, unlike problem 329, here we cannot devise the caching strategy. We cannot store any meaningful solution for the overlapping subproblems. Lets look at example why.

Since 329 is looking for increasing path, same path cannot be used both directions.

0 6 0
5 8 7
0 9 0

Take the above matrix as an example. At position of element 7, if we are looking for longest increasing path, it's 7,8. So at 8 the longest increasing path is not 8, 7. However, if we are finding the maximum sum, the result can come from any direction.

For this problem, for eg., say we started a DFS path from element grid[0][1] (element 6). The max path would be 6 -> 8 -> 9 as explained above. At element 8, (grid[1][1], we would have stored that the max path sum from grid[1][1] would be 8 -> 9, totalling 17.

But now say later in the nested for loop traversal of the grid, we start a DFS path from grid[2][1], (element 9). We can't just use the memoized solution that we stored for grid[1][1] at 8, because it would mean we would revisit 9 which is not allowed. The max path sum at any element is effected by the path of visited elements we have already seen. Thus, there is no real meaningful method/reason to capture this information and use DP.

Video Explanation

Here is the video explanation: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/42V_LlZSpGI" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Using DFS and modifying grid temporarily for visited set

Intuition

• The best path can start at any nonzero cell and depends on which cells have already been visited, so we must explore all paths starting from every gold cell.

Approach

• For each cell with gold, run a DFS that:
  • Adds the current cell's gold to the path sum.
  • Marks the cell visited by setting it to 0 (temporary mutation) to avoid revisits.
  • Recursively explores four neighbors and takes the best continuation.
  • Restores the cell's gold on return (backtracking).
  • Returns the total collected from this starting point.

Code

C++

#include <vector>
#include <algorithm>
using namespace std;

class Solution {
public:
	int getMaximumGold(vector<vector<int>>& grid) {
		int m = grid.size();
		int n = grid[0].size();
		int maxGold = 0;
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				maxGold = max(maxGold, helper(grid, i, j));
			}
		}
		return maxGold;
	}

private:
	const int DIR[4][2] = {{0,-1},{0,1},{-1,0},{1,0}};

	int helper(vector<vector<int>>& grid, int r, int c) {
		if (r < 0 || r >= (int)grid.size() || c < 0 || c >= (int)grid[0].size() || grid[r][c] == 0) return 0;
		int gold = grid[r][c];
		grid[r][c] = 0; // mark visited
		int maxGold = 0;
		for (int k = 0; k < 4; ++k) {
			int nr = r + DIR[k][0];
			int nc = c + DIR[k][1];
			maxGold = max(maxGold, helper(grid, nr, nc));
		}
		grid[r][c] = gold; // restore
		return gold + maxGold;
	}
};

Java

class Solution {
	// left, right, up, down
	private static int[][] DIR = new int[][] { {0, -1}, {0, 1}, {-1, 0}, {1, 0}};
	
	public int getMaximumGold(int[][] grid) {
		int m = grid.length, n = grid[0].length;
		int maxGold = 0;
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				maxGold = Math.max(maxGold, helper(grid, i, j));
			}
		}   
		return maxGold;
	}
	
	private int helper(int[][] grid, int r, int c) {
		if (r < 0 || r == grid.length || c < 0 || c == grid[0].length || grid[r][c] == 0) {
			return 0;
		}
	
		int gold = grid[r][c];
		grid[r][c] = 0; // mark mine as visited by destroying it
		int maxGold = 0;
		for (int i = 0; i < DIR.length; i++) {
			int newR = r + DIR[i][0];
			int newC = c + DIR[i][1];
			maxGold = Math.max(maxGold, helper(grid, newR, newC));
		}
	
		grid[r][c] = gold; // fix the gold mine
		return gold + maxGold;
	}
}

Python

class Solution:
	def getMaximumGold(self, grid: List[List[int]]) -> int:
		m, n = len(grid), len(grid[0])
		max_gold = 0

		def helper(r: int, c: int) -> int:
			if r < 0 or r >= m or c < 0 or c >= n or grid[r][c] == 0:
				return 0
			gold = grid[r][c]
			grid[r][c] = 0
			best = 0
			for dr, dc in ((0,-1),(0,1),(-1,0),(1,0)):
				best = max(best, helper(r+dr, c+dc))
			grid[r][c] = gold
			return gold + best

		for i in range(m):
			for j in range(n):
				max_gold = max(max_gold, helper(i, j))

		return max_gold

Complexity

• ⏰ Time complexity: O(k*4^k), where k <= 25 is the number of cells that have gold. At each point, we can go to 4 neighbours - so, we can split into 4 paths, and that takes O(4^k). We have to do this for at most k times (not m*n times, as we will start DFS only when grid[r][c] has a gold mine, aka non-zero value). Hence O(k*4^k).
• 🧺 Space complexity: O(1) as we temporarily modify grid in place.

Method 2 - DFS using visited set

In this case, we will use visited set.

Intuition

• Using an explicit visited set gives the same backtracking behaviour as mutating the grid, but keeps the input untouched.
• The best path depends on which cells are already visited, so we must try DFS from every gold cell and track visited cells per path.

Approach

• For each cell with non-zero gold, start a DFS with an empty visited set.
• In DFS, return 0 if out-of-bounds, the cell is 0, or already visited; otherwise add the cell to visited, explore 4 neighbours, take the maximum, then remove from visited (backtrack) and return the accumulated sum.
• Track the global maximum across all starts and return it.

Code

C++

#include <vector>
#include <unordered_set>
#include <string>
#include <algorithm>
using namespace std;

class Solution {
public:
	int getMaximumGold(vector<vector<int>>& grid) {
		int m = grid.size(), n = grid[0].size();
		int maxGold = 0;
		for (int i = 0; i < m; ++i) {
			for (int j = 0; j < n; ++j) {
				unordered_set<int> visited;
				maxGold = max(maxGold, helper(grid, i, j, visited));
			}
		}
		return maxGold;
	}

private:
	const int DIR[4][2] = {{0,-1},{0,1},{-1,0},{1,0}};

	int key(int r, int c, int cols) { return r * cols + c; }

	int helper(const vector<vector<int>>& gridConst, int r, int c, unordered_set<int>& visited) {
		int m = gridConst.size(), n = gridConst[0].size();
		if (r < 0 || r >= m || c < 0 || c >= n || gridConst[r][c] == 0) return 0;
		int k = key(r, c, n);
		if (visited.count(k)) return 0;
		visited.insert(k);
		int maxGold = 0;
		for (int i = 0; i < 4; ++i) {
			int nr = r + DIR[i][0];
			int nc = c + DIR[i][1];
			maxGold = max(maxGold, helper(gridConst, nr, nc, visited));
		}
		visited.erase(k);
		return gridConst[r][c] + maxGold;
	}
};

Java

class Solution {
	// left, right, up, down
	private static int[][] DIR = new int[][] { {0, -1}, {0, 1}, {-1, 0}, {1, 0}};
	
	public int getMaximumGold(int[][] grid) {
		int m = grid.length, n = grid[0].length;
		int maxGold = 0;
		for (int i = 0; i < m; i++) {
			for (int j = 0; j < n; j++) {
				maxGold = Math.max(maxGold, helper(grid, i, j, new HashSet<String>()));
			}
		}   
		return maxGold;
	}
	
	private int helper(int[][] grid, int r, int c, Set<String> visited) {
		String key = "" + r + "--" + c;
		if (r < 0 || r == grid.length || c < 0 || c == grid[0].length || grid[r][c] == 0 || visited.contains(key)) {
			return 0;
		}
		visited.add(key);
		int maxGold = 0;
		for (int i = 0; i < DIR.length; i++) {
			int newR = r + DIR[i][0];
			int newC = c + DIR[i][1];
			maxGold = Math.max(maxGold, helper(grid, newR, newC, visited));
		}
		visited.remove(key);
		return grid[r][c] + maxGold;
	}
}

Python

from typing import List, Set, Tuple

class Solution:
	def getMaximumGold(self, grid: List[List[int]]) -> int:
		m, n = len(grid), len(grid[0])
		max_gold = 0

		def helper(r: int, c: int, visited: Set[Tuple[int,int]]) -> int:
			if r < 0 or r >= m or c < 0 or c >= n or grid[r][c] == 0 or (r,c) in visited:
				return 0
			visited.add((r,c))
			best = 0
			for dr, dc in ((0,-1),(0,1),(-1,0),(1,0)):
				best = max(best, helper(r+dr, c+dc, visited))
			visited.remove((r,c))
			return grid[r][c] + best

		for i in range(m):
			for j in range(n):
				max_gold = max(max_gold, helper(i, j, set()))

		return max_gold

Complexity

• ⏰ Time complexity: O(4^k) - Same as previous method.
• 🧺 Space complexity: O(k) - for using visited set.