Path With Minimum Effort
Problem
You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.
A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.
Return the minimum effort required to travel from the top-left cell to the bottom-right cell.
Examples
Example 1:
Input:
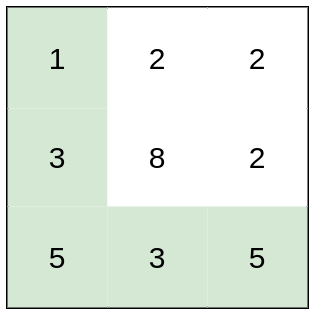
heights = [[1,2,2],[3,8,2],[5,3,5]]
Output:
2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.
Example 2:
Input:
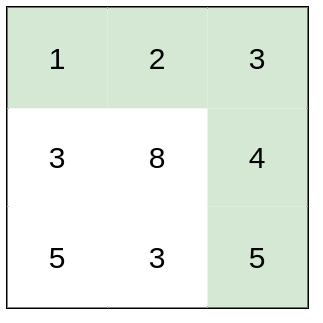
heights = [[1,2,3],[3,8,4],[5,3,5]]
Output:
1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].
Example 3:
Input:
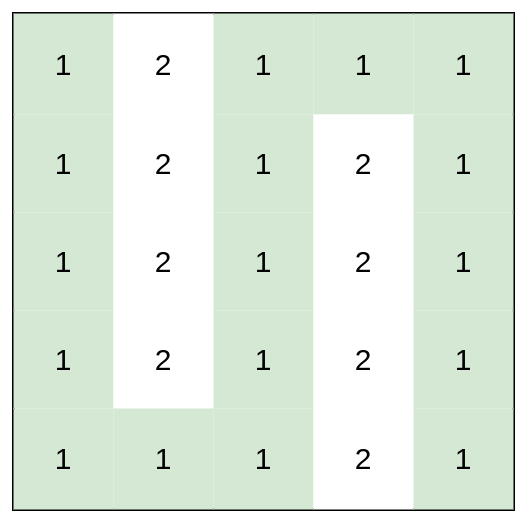
heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output:
0
Explanation: This route does not require any effort.
Solution
Method 1 – Dijkstra's Algorithm
Intuition
The key idea is to use Dijkstra's algorithm to always expand the path with the minimum current effort (maximum height difference so far). This ensures that when we reach the bottom-right cell, the effort is minimized.
Approach
- Use a min-heap to always process the cell with the smallest current effort.
- For each cell, try moving in all four directions.
- For each neighbor, calculate the effort as the maximum of the current effort and the absolute height difference.
- If this effort is less than the previously recorded effort for that cell, update and push to the heap.
- When the bottom-right cell is reached, return the effort.
Code
C++
class Solution {
public:
int minimumEffortPath(vector<vector<int>>& heights) {
int m = heights.size(), n = heights[0].size();
vector<vector<int>> effort(m, vector<int>(n, INT_MAX));
effort[0][0] = 0;
priority_queue<tuple<int,int,int>, vector<tuple<int,int,int>>, greater<>> pq;
pq.emplace(0, 0, 0);
int dirs[4][2] = {{0,1},{1,0},{0,-1},{-1,0}};
while (!pq.empty()) {
auto [e, i, j] = pq.top(); pq.pop();
if (i == m-1 && j == n-1) return e;
for (auto& d : dirs) {
int x = i + d[0], y = j + d[1];
if (x >= 0 && x < m && y >= 0 && y < n) {
int ne = max(e, abs(heights[i][j] - heights[x][y]));
if (ne < effort[x][y]) {
effort[x][y] = ne;
pq.emplace(ne, x, y);
}
}
}
}
return 0;
}
};
Go
func minimumEffortPath(heights [][]int) int {
m, n := len(heights), len(heights[0])
effort := make([][]int, m)
for i := range effort {
effort[i] = make([]int, n)
for j := range effort[i] {
effort[i][j] = 1<<31 - 1
}
}
effort[0][0] = 0
pq := &hp{}
heap.Init(pq)
heap.Push(pq, [3]int{0, 0, 0})
dirs := [][2]int{{0,1},{1,0},{0,-1},{-1,0}}
for pq.Len() > 0 {
e, i, j := (*pq)[0][0], (*pq)[0][1], (*pq)[0][2]
heap.Pop(pq)
if i == m-1 && j == n-1 {
return e
}
for _, d := range dirs {
x, y := i+d[0], j+d[1]
if x >= 0 && x < m && y >= 0 && y < n {
ne := e
if abs(heights[i][j]-heights[x][y]) > ne {
ne = abs(heights[i][j]-heights[x][y])
}
if ne < effort[x][y] {
effort[x][y] = ne
heap.Push(pq, [3]int{ne, x, y})
}
}
}
}
return 0
}
func abs(x int) int { if x < 0 { return -x }; return x }
type hp [][3]int
func (h hp) Len() int { return len(h) }
func (h hp) Less(i, j int) bool { return h[i][0] < h[j][0] }
func (h hp) Swap(i, j int) { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(x interface{}) { *h = append(*h, x.([3]int)) }
func (h *hp) Pop() interface{} { old := *h; x := old[len(old)-1]; *h = old[:len(old)-1]; return x }
Java
class Solution {
public int minimumEffortPath(int[][] heights) {
int m = heights.length, n = heights[0].length;
int[][] effort = new int[m][n];
for (int[] row : effort) Arrays.fill(row, Integer.MAX_VALUE);
effort[0][0] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
pq.offer(new int[]{0, 0, 0});
int[][] dirs = {{0,1},{1,0},{0,-1},{-1,0}};
while (!pq.isEmpty()) {
int[] cur = pq.poll();
int e = cur[0], i = cur[1], j = cur[2];
if (i == m-1 && j == n-1) return e;
for (int[] d : dirs) {
int x = i + d[0], y = j + d[1];
if (x >= 0 && x < m && y >= 0 && y < n) {
int ne = Math.max(e, Math.abs(heights[i][j] - heights[x][y]));
if (ne < effort[x][y]) {
effort[x][y] = ne;
pq.offer(new int[]{ne, x, y});
}
}
}
}
return 0;
}
}
Kotlin
class Solution {
fun minimumEffortPath(heights: Array<IntArray>): Int {
val m = heights.size
val n = heights[0].size
val effort = Array(m) { IntArray(n) { Int.MAX_VALUE } }
effort[0][0] = 0
val pq = java.util.PriorityQueue(compareBy<IntArray> { it[0] })
pq.add(intArrayOf(0, 0, 0))
val dirs = arrayOf(0 to 1, 1 to 0, 0 to -1, -1 to 0)
while (pq.isNotEmpty()) {
val (e, i, j) = pq.remove()
if (i == m-1 && j == n-1) return e
for ((dx, dy) in dirs) {
val x = i + dx
val y = j + dy
if (x in 0 until m && y in 0 until n) {
val ne = maxOf(e, kotlin.math.abs(heights[i][j] - heights[x][y]))
if (ne < effort[x][y]) {
effort[x][y] = ne
pq.add(intArrayOf(ne, x, y))
}
}
}
}
return 0
}
}
Python
class Solution:
def minimumEffortPath(self, heights: list[list[int]]) -> int:
import heapq
m, n = len(heights), len(heights[0])
effort = [[float('inf')] * n for _ in range(m)]
effort[0][0] = 0
h = [(0, 0, 0)]
while h:
e, i, j = heapq.heappop(h)
if i == m-1 and j == n-1:
return e
for dx, dy in ((0,1),(1,0),(0,-1),(-1,0)):
x, y = i+dx, j+dy
if 0 <= x < m and 0 <= y < n:
ne = max(e, abs(heights[i][j] - heights[x][y]))
if ne < effort[x][y]:
effort[x][y] = ne
heapq.heappush(h, (ne, x, y))
return 0
Rust
impl Solution {
pub fn minimum_effort_path(heights: Vec<Vec<i32>>) -> i32 {
use std::collections::BinaryHeap;
let m = heights.len();
let n = heights[0].len();
let mut effort = vec![vec![i32::MAX; n]; m];
effort[0][0] = 0;
let mut h = BinaryHeap::new();
h.push((0, 0, 0));
let dirs = [(0,1),(1,0),(0,-1),(-1,0)];
while let Some((e, i, j)) = h.pop() {
let e = -e;
if i == m-1 && j == n-1 { return e; }
for (dx, dy) in dirs.iter() {
let x = i as i32 + dx;
let y = j as i32 + dy;
if x >= 0 && x < m as i32 && y >= 0 && y < n as i32 {
let (x, y) = (x as usize, y as usize);
let ne = effort[i][j].max((heights[i][j] - heights[x][y]).abs());
if ne < effort[x][y] {
effort[x][y] = ne;
h.push((-ne, x, y));
}
}
}
}
0
}
}
TypeScript
class Solution {
minimumEffortPath(heights: number[][]): number {
const m = heights.length, n = heights[0].length;
const effort = Array.from({length: m}, () => Array(n).fill(Infinity));
effort[0][0] = 0;
const h: [number, number, number][] = [[0, 0, 0]];
while (h.length) {
h.sort((a, b) => a[0] - b[0]);
const [e, i, j] = h.shift()!;
if (i === m-1 && j === n-1) return e;
for (const [dx, dy] of [[0,1],[1,0],[0,-1],[-1,0]]) {
const x = i + dx, y = j + dy;
if (x >= 0 && x < m && y >= 0 && y < n) {
const ne = Math.max(e, Math.abs(heights[i][j] - heights[x][y]));
if (ne < effort[x][y]) {
effort[x][y] = ne;
h.push([ne, x, y]);
}
}
}
}
return 0;
}
}
Complexity
- ⏰ Time complexity:
O(mn log(mn)), where m and n are the grid dimensions; Dijkstra's algorithm dominates. - 🧺 Space complexity:
O(mn), for the effort matrix and heap.