Problem

A maze consists of n rooms numbered from 1 to n, and some rooms are connected by corridors. You are given a 2D integer array corridors where corridors[i] = [room1i, room2i] indicates that there is a corridor connecting room1i and room2i, allowing a person in the maze to go from room1i to room2i and vice versa.

The designer of the maze wants to know how confusing the maze is. The confusion score of the maze is the number of different cycles of length 3.

  • For example, 1 -> 2 -> 3 -> 1 is a cycle of length 3, but 1 -> 2 -> 3 -> 4 and 1 -> 2 -> 3 -> 2 -> 1 are not.

Two cycles are considered to be different if one or more of the rooms visited in the first cycle is not in the second cycle.

Return the confusion****score of the maze.

Examples

Example 1:

1
2
3
4
5
6
7

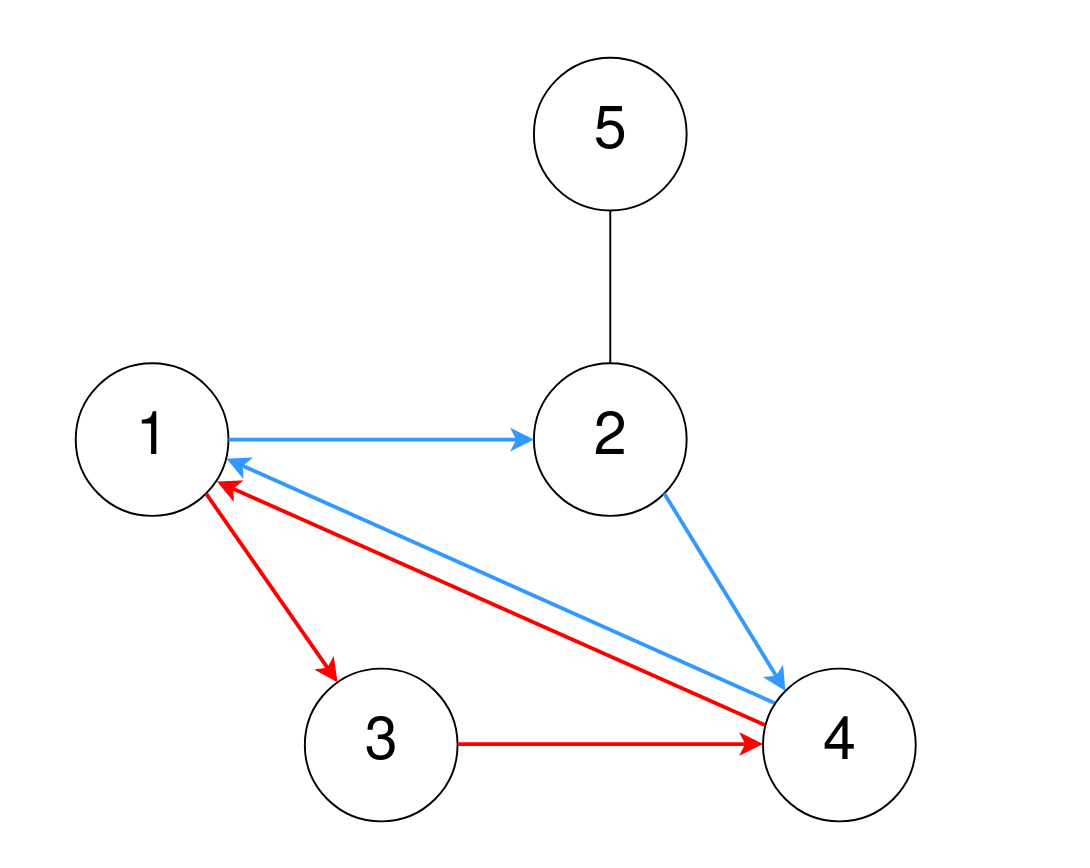
Input: n = 5, corridors = [[1,2],[5,2],[4,1],[2,4],[3,1],[3,4]]
Output: 2
Explanation:
One cycle of length 3 is 4 -> 1 -> 3 -> 4, denoted in red.
Note that this is the same cycle as 3 -> 4 -> 1 -> 3 or 1 -> 3 -> 4 -> 1 because the rooms are the same.
Another cycle of length 3 is 1 -> 2 -> 4 -> 1, denoted in blue.
Thus, there are two different cycles of length 3.

Example 2:

1
2
3
4

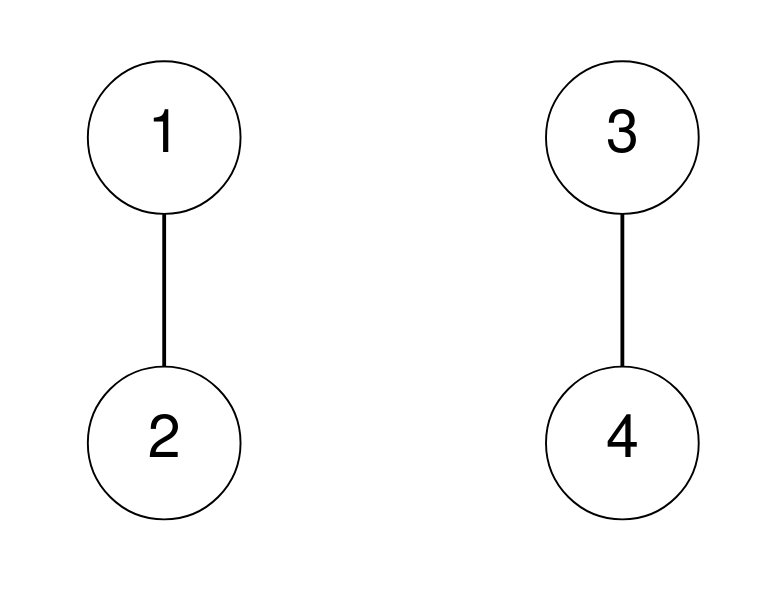
Input: n = 4, corridors = [[1,2],[3,4]]
Output: 0
Explanation:
There are no cycles of length 3.

Constraints:

  • 2 <= n <= 1000
  • 1 <= corridors.length <= 5 * 10^4
  • corridors[i].length == 2
  • 1 <= room1i, room2i <= n
  • room1i != room2i
  • There are no duplicate corridors.

Solution

Method 1 - Edge-wise Common-Neighbor Triangle Counting

Intuition

We need to count the number of unique cycles of length 3 (triangles) in an undirected graph. For each pair of connected nodes, count the number of common neighbors. Each triangle is counted once per edge when we sum common neighbors across edges; since each triangle has 3 edges, it will be counted 3 times in total, so divide the final sum by 3 to get the number of distinct triangles.

Approach

Build an adjacency set for each node. For each edge (u, v), count the number of common neighbors between u and v (this equals the number of triangles that include edge (u, v)). Sum this for all edges, then divide the total by 3 to obtain the number of unique length-3 cycles.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

#include <vector>
#include <unordered_set>
using namespace std;
class Solution {
public:
    int numberOfPaths(int n, vector<vector<int>>& corridors) {
        vector<unordered_set<int>> g(n+1);
        for (auto& e : corridors) {
            g[e[0]].insert(e[1]);
            g[e[1]].insert(e[0]);
        }
        int cnt = 0;
        for (int u = 1; u <= n; ++u) {
            for (int v : g[u]) if (u < v) {
                for (int w : g[u]) if (w > u && w != v && g[v].count(w)) cnt++;
            }
        }
        return cnt / 3;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

func numberOfPaths(n int, corridors [][]int) int {
    g := make([]map[int]struct{}, n+1)
    for i := range g { g[i] = map[int]struct{}{} }
    for _, e := range corridors {
        g[e[0]][e[1]] = struct{}{}
        g[e[1]][e[0]] = struct{}{}
    }
    cnt := 0
    for u := 1; u <= n; u++ {
        for v := range g[u] {
            if u < v {
                for w := range g[u] {
                    if w > u && w != v {
                        if _, ok := g[v][w]; ok { cnt++ }
                    }
                }
            }
        }
    }
    return cnt / 3
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import java.util.*;
class Solution {
    public int numberOfPaths(int n, int[][] corridors) {
        List<Set<Integer>> g = new ArrayList<>();
        for (int i = 0; i <= n; i++) g.add(new HashSet<>());
        for (int[] e : corridors) {
            g.get(e[0]).add(e[1]);
            g.get(e[1]).add(e[0]);
        }
        int cnt = 0;
        for (int u = 1; u <= n; u++) {
            for (int v : g.get(u)) if (u < v) {
                for (int w : g.get(u)) if (w > u && w != v && g.get(v).contains(w)) cnt++;
            }
        }
        return cnt / 3;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    fun numberOfPaths(n: Int, corridors: Array<IntArray>): Int {
        val g = Array(n+1) { mutableSetOf<Int>() }
        for (e in corridors) {
            g[e[0]].add(e[1])
            g[e[1]].add(e[0])
        }
        var cnt = 0
        for (u in 1..n) {
            for (v in g[u]) if (u < v) {
                for (w in g[u]) if (w > u && w != v && w in g[v]) cnt++
            }
        }
        return cnt / 3
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

def numberOfPaths(n: int, corridors: list[list[int]]) -> int:
    from collections import defaultdict
    g = defaultdict(set)
    for u, v in corridors:
        g[u].add(v)
        g[v].add(u)
    cnt = 0
    for u in range(1, n+1):
        for v in g[u]:
            if u < v:
                for w in g[u]:
                    if w > u and w != v and w in g[v]:
                        cnt += 1
    return cnt // 3
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

use std::collections::HashSet;
fn number_of_paths(n: usize, corridors: Vec<Vec<usize>>) -> i32 {
    let mut g = vec![HashSet::new(); n+1];
    for e in corridors.iter() {
        g[e[0]].insert(e[1]);
        g[e[1]].insert(e[0]);
    }
    let mut cnt = 0;
    for u in 1..=n {
        for &v in &g[u] {
            if u < v {
                for &w in &g[u] {
                    if w > u && w != v && g[v].contains(&w) { cnt += 1; }
                }
            }
        }
    }
    cnt / 3
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

function numberOfPaths(n: number, corridors: number[][]): number {
    const g: Set<number>[] = Array.from({length: n+1}, () => new Set());
    for (const [u, v] of corridors) {
        g[u].add(v);
        g[v].add(u);
    }
    let cnt = 0;
    for (let u = 1; u <= n; u++) {
        for (const v of g[u]) if (u < v) {
            for (const w of g[u]) if (w > u && w !== v && g[v].has(w)) cnt++;
        }
    }
    return Math.floor(cnt / 3);
}

Complexity

  • ⏰ Time complexity: O(M * D) – For each of the M edges we iterate over the neighbors of one endpoint (average degree D) and check membership in the other’s adjacency set.
  • 🧺 Space complexity: O(N + M) – We store adjacency sets for all nodes; in the worst case of a dense graph this can be O(N^2).