problemhardalgorithmsleetcode-1388leetcode 1388leetcode1388

Pizza With 3n Slices

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:

  • You will pick any pizza slice.
  • Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
  • Your friend Bob will pick the next slice in the clockwise direction of your pick.
  • Repeat until there are no more slices of pizzas.

Given an integer array slices that represent the sizes of the pizza slices in a clockwise direction, return the maximum possible sum of slice sizes that you can pick.

Examples

Example 1

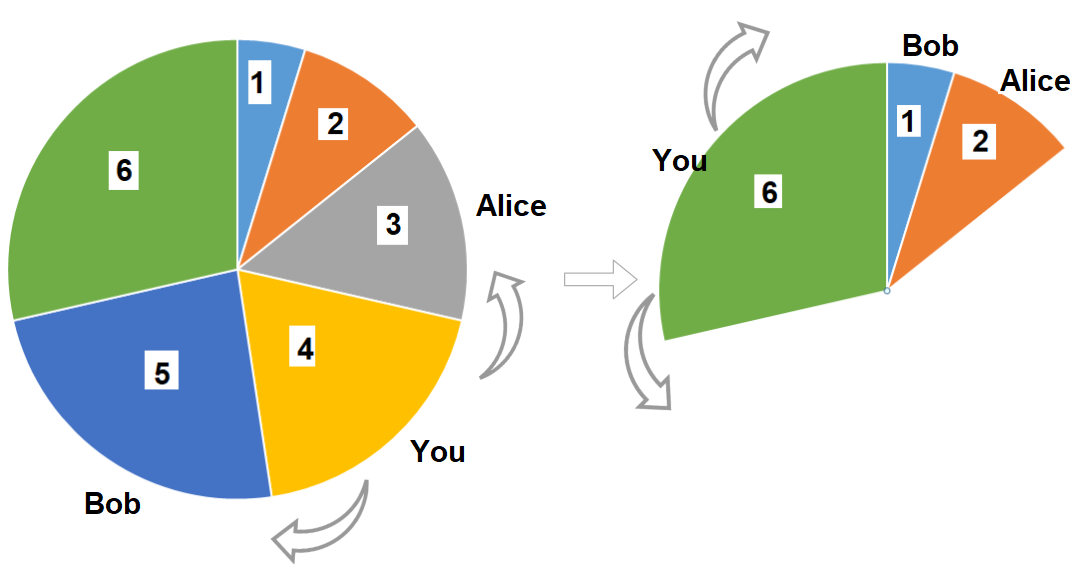
Input: slices = [1,2,3,4,5,6]
Output: 10
Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.

Example 2

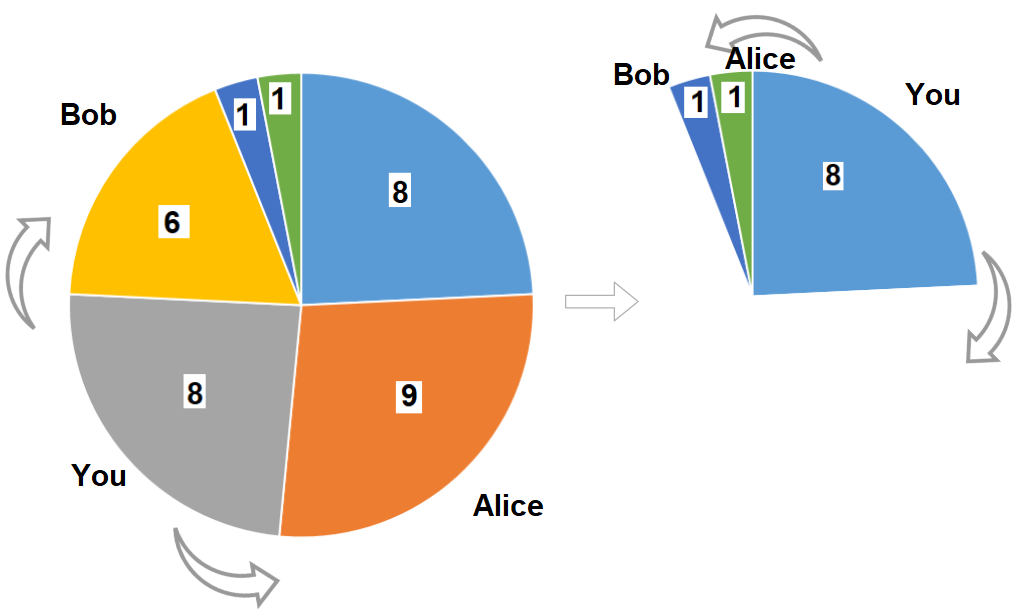
Input: slices = [8,9,8,6,1,1]
Output: 16
Explanation: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.

Constraints

  • 3 * n == slices.length
  • 1 <= slices.length <= 500
  • 1 <= slices[i] <= 1000

Solution

Method 1 – Dynamic Programming with Circular Array

Intuition

Since the pizza is circular and you must pick n slices out of 3n, with no two picked slices adjacent, this is a variation of the "House Robber II" problem. We use dynamic programming to maximize the sum, considering two cases: exclude the first slice or exclude the last slice, to avoid picking both ends.

Approach

  1. Let n = slices.length / 3.
  2. Define a helper DP function to pick k slices from a linear array with no two adjacent.
  3. Run the DP for slices[0..n3-2] (exclude last) and slices[1..n3-1] (exclude first).
  4. Return the maximum of the two results.

Code

C++
class Solution {
public:
    int maxSizeSlices(vector<int>& slices) {
        int n = slices.size() / 3;
        auto dp = [&](vector<int>& arr) {
            int m = arr.size();
            vector<vector<int>> f(m+1, vector<int>(n+1, 0));
            for (int i = 1; i <= m; ++i) {
                for (int k = 1; k <= n; ++k) {
                    f[i][k] = max(f[i-1][k], f[i-2][k-1] + arr[i-1]);
                }
            }
            return f[m][n];
        };
        vector<int> a(slices.begin(), slices.end()-1), b(slices.begin()+1, slices.end());
        return max(dp(a), dp(b));
    }
};
Go
func maxSizeSlices(slices []int) int {
    n := len(slices) / 3
    dp := func(arr []int) int {
        m := len(arr)
        f := make([][]int, m+1)
        for i := range f {
            f[i] = make([]int, n+1)
        }
        for i := 1; i <= m; i++ {
            for k := 1; k <= n; k++ {
                f[i][k] = max(f[i-1][k], f[max(0,i-2)][k-1]+arr[i-1])
            }
        }
        return f[m][n]
    }
    a := slices[:len(slices)-1]
    b := slices[1:]
    return max(dp(a), dp(b))
}
func max(a, b int) int { if a > b { return a }; return b }
Java
class Solution {
    public int maxSizeSlices(int[] slices) {
        int n = slices.length / 3;
        return Math.max(dp(slices, 0, slices.length-2, n), dp(slices, 1, slices.length-1, n));
    }
    int dp(int[] arr, int l, int r, int k) {
        int m = r-l+1;
        int[][] f = new int[m+1][k+1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= k; j++) {
                f[i][j] = Math.max(f[i-1][j], f[Math.max(0,i-2)][j-1]+arr[l+i-1]);
            }
        }
        return f[m][k];
    }
}
Kotlin
class Solution {
    fun maxSizeSlices(slices: IntArray): Int {
        val n = slices.size / 3
        fun dp(arr: IntArray): Int {
            val m = arr.size
            val f = Array(m+1) { IntArray(n+1) }
            for (i in 1..m) {
                for (k in 1..n) {
                    f[i][k] = maxOf(f[i-1][k], f[maxOf(0,i-2)][k-1]+arr[i-1])
                }
            }
            return f[m][n]
        }
        val a = slices.sliceArray(0 until slices.size-1)
        val b = slices.sliceArray(1 until slices.size)
        return maxOf(dp(a), dp(b))
    }
}
Python
def maxSizeSlices(slices: list[int]) -> int:
    def dp(arr: list[int], k: int) -> int:
        m = len(arr)
        f = [[0]*(k+1) for _ in range(m+1)]
        for i in range(1, m+1):
            for j in range(1, k+1):
                f[i][j] = max(f[i-1][j], f[max(0,i-2)][j-1]+arr[i-1])
        return f[m][k]
    n = len(slices)//3
    return max(dp(slices[:-1], n), dp(slices[1:], n))
Rust
impl Solution {
    pub fn max_size_slices(slices: Vec<i32>) -> i32 {
        fn dp(arr: &[i32], k: usize) -> i32 {
            let m = arr.len();
            let mut f = vec![vec![0; k+1]; m+1];
            for i in 1..=m {
                for j in 1..=k {
                    f[i][j] = f[i-1][j].max(f[i.saturating_sub(2)][j-1]+arr[i-1]);
                }
            }
            f[m][k]
        }
        let n = slices.len()/3;
        dp(&slices[..slices.len()-1], n).max(dp(&slices[1..], n))
    }
}
TypeScript
class Solution {
    maxSizeSlices(slices: number[]): number {
        const n = slices.length / 3;
        function dp(arr: number[]): number {
            const m = arr.length;
            const f: number[][] = Array.from({length: m+1}, () => Array(n+1).fill(0));
            for (let i = 1; i <= m; i++) {
                for (let k = 1; k <= n; k++) {
                    f[i][k] = Math.max(f[i-1][k], f[Math.max(0,i-2)][k-1]+arr[i-1]);
                }
            }
            return f[m][n];
        }
        const a = slices.slice(0, slices.length-1);
        const b = slices.slice(1);
        return Math.max(dp(a), dp(b));
    }
}

Complexity

  • ⏰ Time complexity: O(n^2), where n is the number of slices.
  • 🧺 Space complexity: O(n^2), for the DP table.

Comments