Point in Polygon
Problem
You are given a list of N points (x1, y1), (x2, y2), ..., (xN, yN) representing a polygon. You can assume these points are given in order; that is, you can construct the polygon by connecting point 1 to point 2, point 2 to point 3, and so on, finally looping around to connect point N to point 1.
Determine if a new point p lies inside this polygon. (If p is on the boundary of the polygon, you should return False).
Background
Known as Point-In-Polygon problem, testing whether a point lies inside a polygon is a classic literature problem in computational geometry.
A simple test to check whether a point p = {x, y} lies inside a given polygon is to extend one of its dimensions to infinity:
p_inf = {+∞, y}
and do a line segments intersection test between p p_inf and each one of the edges of the polygon. If the count of the intersections is odd, the point lies inside the polygon.
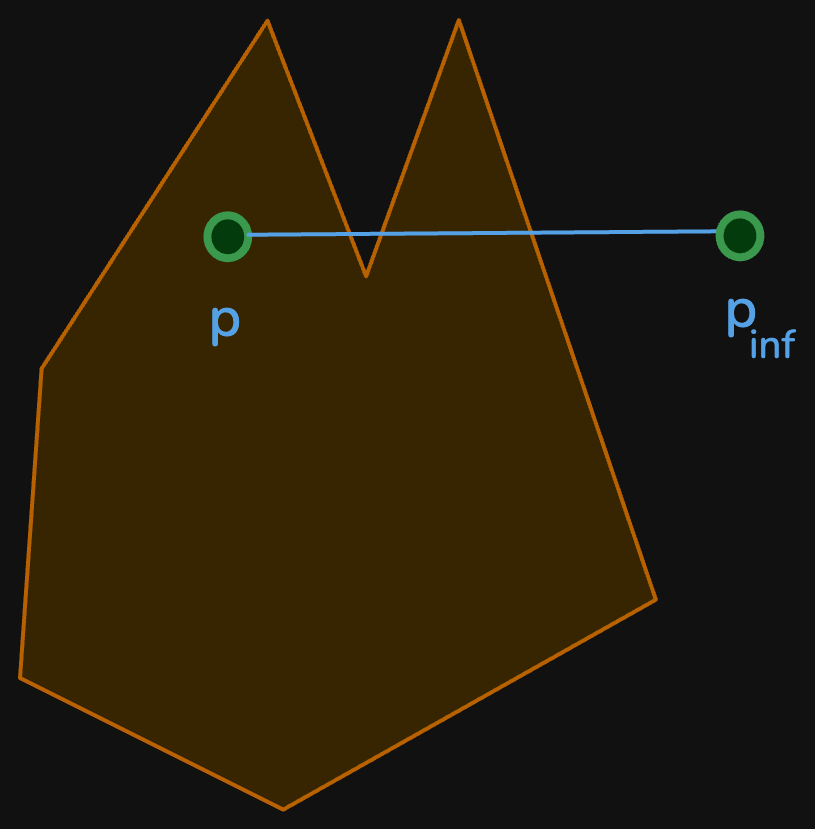
Special attention deserve two cases:
- when segment
p p_infhas a successful intersection test andpis found collinear to the polygon edge: ifplies in the polygon edge segment, any further check can be skipped since the point lies on the border of the polygon - when the
to_infinitysegment crosses one or more vertices of the polygon the intersection has to be counted once
Examples
Example 1
Input:
polygon = [(0, 0), (4, 0), (4, 4), (0, 4)]
point = (2, 2)
Output:
true
Explanation:
The polygon forms a square with corners at (0,0), (4,0), (4,4), and (0,4). The point (2,2) is inside this square.
Example 2
Input:
polygon = [(0, 0), (4, 0), (4, 4), (0, 4)]
point = (4, 2)
Output:
false
Explanation:
The point (4,2) lies exactly on the boundary of the square (on the right edge), so we return false as specified.
Example 3
Input:
polygon = [(0, 0), (3, 1), (2, 4), (-1, 3)]
point = (1, 2)
Output:
true
Explanation:
The polygon is an irregular quadrilateral, and the point (1,2) lies strictly inside it.
Example 4
Input:
polygon = [(0, 0), (3, 1), (2, 4), (-1, 3)]
point = (5, 5)
Output:
false
Explanation:
The point (5,5) is completely outside the polygon boundaries.
Solution
Method 1 - Ray Casting Algorithm
Intuition
The ray casting algorithm works by casting a ray from the test point in any direction (typically horizontal to the right) and counting how many times it intersects with the polygon edges. If the number of intersections is odd, the point is inside; if even, it's outside. This is based on the mathematical principle that to enter a closed shape, you must cross its boundary an odd number of times.
Approach
- Cast a horizontal ray from the test point extending to the right (to infinity)
- Count intersections with each edge of the polygon
- For each edge from vertex i to vertex i+1:
- Check if the ray intersects this edge
- Handle special cases like horizontal edges and vertices
- An intersection occurs when:
- The ray's y-coordinate is between the edge's y-coordinates
- The intersection point's x-coordinate is to the right of the test point
- Return true if the intersection count is odd, false if even
- Special handling for boundary points: return false if point lies exactly on any edge
Code
C++
class Solution {
public:
bool pointInPolygon(vector<pair<double, double>>& polygon, pair<double, double> point) {
int n = polygon.size();
if (n < 3) return false;
double px = point.first, py = point.second;
bool inside = false;
for (int i = 0; i < n; i++) {
int j = (i + 1) % n;
double xi = polygon[i].first, yi = polygon[i].second;
double xj = polygon[j].first, yj = polygon[j].second;
// Check if point is on the edge
if (isOnEdge(xi, yi, xj, yj, px, py)) {
return false;
}
// Ray casting check
if (((yi > py) != (yj > py)) &&
(px < (xj - xi) * (py - yi) / (yj - yi) + xi)) {
inside = !inside;
}
}
return inside;
}
private:
bool isOnEdge(double x1, double y1, double x2, double y2, double px, double py) {
double eps = 1e-9;
// Check if point is within bounding box of the edge
if (px < min(x1, x2) - eps || px > max(x1, x2) + eps ||
py < min(y1, y2) - eps || py > max(y1, y2) + eps) {
return false;
}
// Check if point lies on the line segment
double cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1);
return abs(cross) < eps;
}
};
Go
import "math"
func pointInPolygon(polygon [][]float64, point []float64) bool {
n := len(polygon)
if n < 3 {
return false
}
px, py := point[0], point[1]
inside := false
for i := 0; i < n; i++ {
j := (i + 1) % n
xi, yi := polygon[i][0], polygon[i][1]
xj, yj := polygon[j][0], polygon[j][1]
// Check if point is on the edge
if isOnEdge(xi, yi, xj, yj, px, py) {
return false
}
// Ray casting check
if ((yi > py) != (yj > py)) &&
(px < (xj-xi)*(py-yi)/(yj-yi)+xi) {
inside = !inside
}
}
return inside
}
func isOnEdge(x1, y1, x2, y2, px, py float64) bool {
eps := 1e-9
// Check if point is within bounding box of the edge
if px < math.Min(x1, x2)-eps || px > math.Max(x1, x2)+eps ||
py < math.Min(y1, y2)-eps || py > math.Max(y1, y2)+eps {
return false
}
// Check if point lies on the line segment
cross := (py-y1)*(x2-x1) - (px-x1)*(y2-y1)
return math.Abs(cross) < eps
}
func min(a, b float64) float64 {
if a < b {
return a
}
return b
}
func max(a, b float64) float64 {
if a > b {
return a
}
return b
}
Java
class Solution {
public boolean pointInPolygon(double[][] polygon, double[] point) {
int n = polygon.length;
if (n < 3) return false;
double px = point[0], py = point[1];
boolean inside = false;
for (int i = 0; i < n; i++) {
int j = (i + 1) % n;
double xi = polygon[i][0], yi = polygon[i][1];
double xj = polygon[j][0], yj = polygon[j][1];
// Check if point is on the edge
if (isOnEdge(xi, yi, xj, yj, px, py)) {
return false;
}
// Ray casting check
if (((yi > py) != (yj > py)) &&
(px < (xj - xi) * (py - yi) / (yj - yi) + xi)) {
inside = !inside;
}
}
return inside;
}
private boolean isOnEdge(double x1, double y1, double x2, double y2, double px, double py) {
double eps = 1e-9;
// Check if point is within bounding box of the edge
if (px < Math.min(x1, x2) - eps || px > Math.max(x1, x2) + eps ||
py < Math.min(y1, y2) - eps || py > Math.max(y1, y2) + eps) {
return false;
}
// Check if point lies on the line segment
double cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1);
return Math.abs(cross) < eps;
}
}
Python
class Solution:
def pointInPolygon(self, polygon: List[List[float]], point: List[float]) -> bool:
n = len(polygon)
if n < 3:
return False
px, py = point[0], point[1]
inside = False
for i in range(n):
j = (i + 1) % n
xi, yi = polygon[i][0], polygon[i][1]
xj, yj = polygon[j][0], polygon[j][1]
# Check if point is on the edge
if self._is_on_edge(xi, yi, xj, yj, px, py):
return False
# Ray casting check
if ((yi > py) != (yj > py)) and \
(px < (xj - xi) * (py - yi) / (yj - yi) + xi):
inside = not inside
return inside
def _is_on_edge(self, x1: float, y1: float, x2: float, y2: float,
px: float, py: float) -> bool:
eps = 1e-9
# Check if point is within bounding box of the edge
if (px < min(x1, x2) - eps or px > max(x1, x2) + eps or
py < min(y1, y2) - eps or py > max(y1, y2) + eps):
return False
# Check if point lies on the line segment
cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1)
return abs(cross) < eps
Complexity
- ⏰ Time complexity:
O(n), where n is the number of vertices in the polygon. We need to check each edge exactly once - 🧺 Space complexity:
O(1), only using constant extra space for variables
Method 2 - Winding Number Algorithm
Intuition
The winding number algorithm calculates how many times the polygon winds around the test point. If the winding number is non-zero, the point is inside; if zero, it's outside. This method is more robust for complex polygons and handles edge cases better than ray casting.
Approach
- Initialize winding number to 0
- For each edge of the polygon:
- Determine if the edge crosses the horizontal line through the test point
- If it crosses from below to above, increment winding number
- If it crosses from above to below, decrement winding number
- Check if the point lies exactly on any edge (return false if true)
- Return true if winding number is non-zero, false otherwise
- Use cross product to determine the side of the point relative to each edge
Code
C++
class Solution {
public:
bool pointInPolygon(vector<pair<double, double>>& polygon, pair<double, double> point) {
int n = polygon.size();
if (n < 3) return false;
double px = point.first, py = point.second;
int windingNum = 0;
for (int i = 0; i < n; i++) {
int j = (i + 1) % n;
double x1 = polygon[i].first, y1 = polygon[i].second;
double x2 = polygon[j].first, y2 = polygon[j].second;
// Check if point is on the edge
if (isOnEdge(x1, y1, x2, y2, px, py)) {
return false;
}
// Winding number calculation
if (y1 <= py) {
if (y2 > py && isLeft(x1, y1, x2, y2, px, py) > 0) {
windingNum++;
}
} else {
if (y2 <= py && isLeft(x1, y1, x2, y2, px, py) < 0) {
windingNum--;
}
}
}
return windingNum != 0;
}
private:
double isLeft(double x1, double y1, double x2, double y2, double px, double py) {
return (x2 - x1) * (py - y1) - (px - x1) * (y2 - y1);
}
bool isOnEdge(double x1, double y1, double x2, double y2, double px, double py) {
double eps = 1e-9;
if (px < min(x1, x2) - eps || px > max(x1, x2) + eps ||
py < min(y1, y2) - eps || py > max(y1, y2) + eps) {
return false;
}
double cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1);
return abs(cross) < eps;
}
};
Go
func pointInPolygonWinding(polygon [][]float64, point []float64) bool {
n := len(polygon)
if n < 3 {
return false
}
px, py := point[0], point[1]
windingNum := 0
for i := 0; i < n; i++ {
j := (i + 1) % n
x1, y1 := polygon[i][0], polygon[i][1]
x2, y2 := polygon[j][0], polygon[j][1]
// Check if point is on the edge
if isOnEdge(x1, y1, x2, y2, px, py) {
return false
}
// Winding number calculation
if y1 <= py {
if y2 > py && isLeft(x1, y1, x2, y2, px, py) > 0 {
windingNum++
}
} else {
if y2 <= py && isLeft(x1, y1, x2, y2, px, py) < 0 {
windingNum--
}
}
}
return windingNum != 0
}
func isLeft(x1, y1, x2, y2, px, py float64) float64 {
return (x2-x1)*(py-y1) - (px-x1)*(y2-y1)
}
Java
class Solution {
public boolean pointInPolygonWinding(double[][] polygon, double[] point) {
int n = polygon.length;
if (n < 3) return false;
double px = point[0], py = point[1];
int windingNum = 0;
for (int i = 0; i < n; i++) {
int j = (i + 1) % n;
double x1 = polygon[i][0], y1 = polygon[i][1];
double x2 = polygon[j][0], y2 = polygon[j][1];
// Check if point is on the edge
if (isOnEdge(x1, y1, x2, y2, px, py)) {
return false;
}
// Winding number calculation
if (y1 <= py) {
if (y2 > py && isLeft(x1, y1, x2, y2, px, py) > 0) {
windingNum++;
}
} else {
if (y2 <= py && isLeft(x1, y1, x2, y2, px, py) < 0) {
windingNum--;
}
}
}
return windingNum != 0;
}
private double isLeft(double x1, double y1, double x2, double y2, double px, double py) {
return (x2 - x1) * (py - y1) - (px - x1) * (y2 - y1);
}
private boolean isOnEdge(double x1, double y1, double x2, double y2, double px, double py) {
double eps = 1e-9;
if (px < Math.min(x1, x2) - eps || px > Math.max(x1, x2) + eps ||
py < Math.min(y1, y2) - eps || py > Math.max(y1, y2) + eps) {
return false;
}
double cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1);
return Math.abs(cross) < eps;
}
}
Python
class Solution:
def pointInPolygonWinding(self, polygon: List[List[float]], point: List[float]) -> bool:
n = len(polygon)
if n < 3:
return False
px, py = point[0], point[1]
winding_num = 0
for i in range(n):
j = (i + 1) % n
x1, y1 = polygon[i][0], polygon[i][1]
x2, y2 = polygon[j][0], polygon[j][1]
# Check if point is on the edge
if self._is_on_edge(x1, y1, x2, y2, px, py):
return False
# Winding number calculation
if y1 <= py:
if y2 > py and self._is_left(x1, y1, x2, y2, px, py) > 0:
winding_num += 1
else:
if y2 <= py and self._is_left(x1, y1, x2, y2, px, py) < 0:
winding_num -= 1
return winding_num != 0
def _is_left(self, x1: float, y1: float, x2: float, y2: float,
px: float, py: float) -> float:
return (x2 - x1) * (py - y1) - (px - x1) * (y2 - y1)
def _is_on_edge(self, x1: float, y1: float, x2: float, y2: float,
px: float, py: float) -> bool:
eps = 1e-9
if (px < min(x1, x2) - eps or px > max(x1, x2) + eps or
py < min(y1, y2) - eps or py > max(y1, y2) + eps):
return False
cross = (py - y1) * (x2 - x1) - (px - x1) * (y2 - y1)
return abs(cross) < eps
Complexity
- ⏰ Time complexity:
O(n), where n is the number of vertices in the polygon. We process each edge exactly once - 🧺 Space complexity:
O(1), only using constant extra space for the winding number and temporary variables
Analysis
Both methods solve the point-in-polygon problem effectively:
- Method 1 (Ray Casting): Simpler to understand and implement, based on counting intersections
- Method 2 (Winding Number): More mathematically robust, handles complex polygons better
Key considerations:
- Both methods correctly handle the boundary condition by returning
falsefor points on edges - Floating-point precision is handled using an epsilon value for edge detection
- The algorithms work for both convex and concave polygons
- Time complexity is optimal as we must examine each edge at least once
Advanced Implementation
Method 3 - Detailed Ray Casting with Edge Cases
This implementation provides comprehensive handling of edge cases including vertex intersections, collinear points, and special geometric configurations.
Code
C++
#include <iostream>
#include <string>
#include <vector>
#include <iterator>
#include <algorithm>
#include <unordered_set>
using namespace std;
// NB: max_int would cause overflow in the orientation test
const int INF = 100000;
struct Point {
int x, y;
bool operator==(const Point& other) const {
return (x == other.x && y == other.y);
}
};
namespace std {
template <> struct hash<Point> {
size_t operator()(const Point& p) const {
return (p.x * 41) ^ p.y;
}
};
}
ostream& operator<<(ostream& os, const Point& p) {
os << "{" << p.x << ";" << p.y << "}";
return os;
}
ostream& operator<<(ostream& os, const vector<Point>& p) {
os << "{";
copy(p.begin(), p.end(), ostream_iterator<Point>(os));
os << "}";
return os;
}
int orientation(const Point& p1, const Point& p2, const Point& q1) {
int val = (p2.y - p1.y) * (q1.x - p2.x) - (q1.y - p2.y) * (p2.x - p1.x);
if (val == 0)
return 0;
else
return (val < 0) ? -1 : 1;
}
// Returns true if q lies on p1-p2
bool onSegment(const Point& p1, const Point& p2, const Point& q) {
if (min(p1.x, p2.x) <= q.x && q.x <= max(p1.x, p2.x)
&& min(p1.y, p2.y) <= q.y && q.y <= max(p1.y, p2.y))
return true;
else
return false;
}
bool intersectionTest(const Point& p1, const Point& p2,
const Point& p3, const Point& p4) {
int o1 = orientation(p1, p2, p3);
int o2 = orientation(p1, p2, p4);
int o3 = orientation(p3, p4, p1);
int o4 = orientation(p3, p4, p2);
// General case
if (o1 != o2 && o3 != o4)
return true;
// Special cases
if (o1 == 0 && onSegment(p1, p2, p3))
return true;
if (o2 == 0 && onSegment(p1, p2, p4))
return true;
if (o3 == 0 && onSegment(p3, p4, p1))
return true;
if (o4 == 0 && onSegment(p3, p4, p2))
return true;
return false;
}
bool pointInPolygon(const Point& p, const vector<Point>& polygon) {
if (polygon.size() < 3)
return false; // Flawed polygon
Point PtoInfinity = { INF, p.y };
int intersectionsCount = 0;
int i = 0, j = i + 1;
// Same Y coordinate points have to be counted once
unordered_set<Point> sameYcoordPoints;
do {
if (intersectionTest(p, PtoInfinity, polygon[i], polygon[j]) == true) {
bool invalidIntersection = false;
if (p.y == polygon[i].y || p.y == polygon[j].y) {
auto res = sameYcoordPoints.find(polygon[i]);
// Possible collision
if (res != sameYcoordPoints.end() && *res == polygon[i])
invalidIntersection = true;
res = sameYcoordPoints.find(polygon[j]);
// Possible collision
if (res != sameYcoordPoints.end() && *res == polygon[i])
invalidIntersection = true;
if (p.y == polygon[i].y)
sameYcoordPoints.emplace(polygon[i]);
else if (p.y == polygon[j].y)
sameYcoordPoints.emplace(polygon[j]);
}
if (!invalidIntersection) {
++intersectionsCount;
if (orientation(polygon[i], polygon[j], p) == 0) { // Collinear
if (onSegment(polygon[i], polygon[j], p) == true)
return true;
else {
// Exception case when point is collinear but not on segment
// e.g.
// * ************
// / \
// k w
// The collinear segment is worth 0 if k and w have the same
// vertical direction
int k = (((i - 1) >= 0) ? // Negative wraparound
(i - 1) % static_cast<int>(polygon.size()) :
static_cast<int>(polygon.size()) + (i - 1));
int w = ((j + 1) % polygon.size());
if ((polygon[k].y <= polygon[i].y && polygon[w].y <= polygon[j].y)
|| (polygon[k].y >= polygon[i].y && polygon[w].y >= polygon[j].y))
--intersectionsCount;
}
}
}
}
i = ((i + 1) % polygon.size());
j = ((j + 1) % polygon.size());
} while (i != 0);
return (intersectionsCount % 2 != 0);
}
// Example usage
void demonstratePointInPolygon() {
auto printPointInPolygon = [](auto p, auto& polygon) {
cout << boolalpha << "Point " << p << " lies in polygon " << polygon <<
" - " << pointInPolygon(p, polygon) << endl;
};
vector<Point> polygon = { { 2,1 },{ 3,2 },{ 2,3 } };
Point p = { 1,2 };
printPointInPolygon(p, polygon);
polygon = { { 0, 0 },{ 5, 0 },{ 10, 10 },{ 5, 10 } };
p = { 3, 3 };
printPointInPolygon(p, polygon);
p = { 4, 10 };
printPointInPolygon(p, polygon);
polygon = { { 0, 0 },{ -5, 0 },{ -10, -10 } };
p = { 0, -2 };
printPointInPolygon(p, polygon);
}
Key Features of Advanced Implementation
- Vertex Intersection Handling: Uses hash set to track vertices that lie on the same horizontal line as the test point
- Collinear Point Detection: Special handling when the test point is collinear with polygon edges
- Integer Arithmetic: Uses integer coordinates to avoid floating-point precision issues
- Edge Case Management: Comprehensive handling of degenerate cases and boundary conditions
- Efficient Wraparound: Proper modular arithmetic for polygon edge traversal
Complexity
- ⏰ Time complexity:
O(n), where n is the number of vertices in the polygon - 🧺 Space complexity:
O(k), where k is the number of vertices with the same y-coordinate as the test point