problemeasyalgorithmsleetcode-883leetcode 883leetcode883

Projection Area of 3D Shapes

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).

We view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the "shadow" when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Examples

Example 1


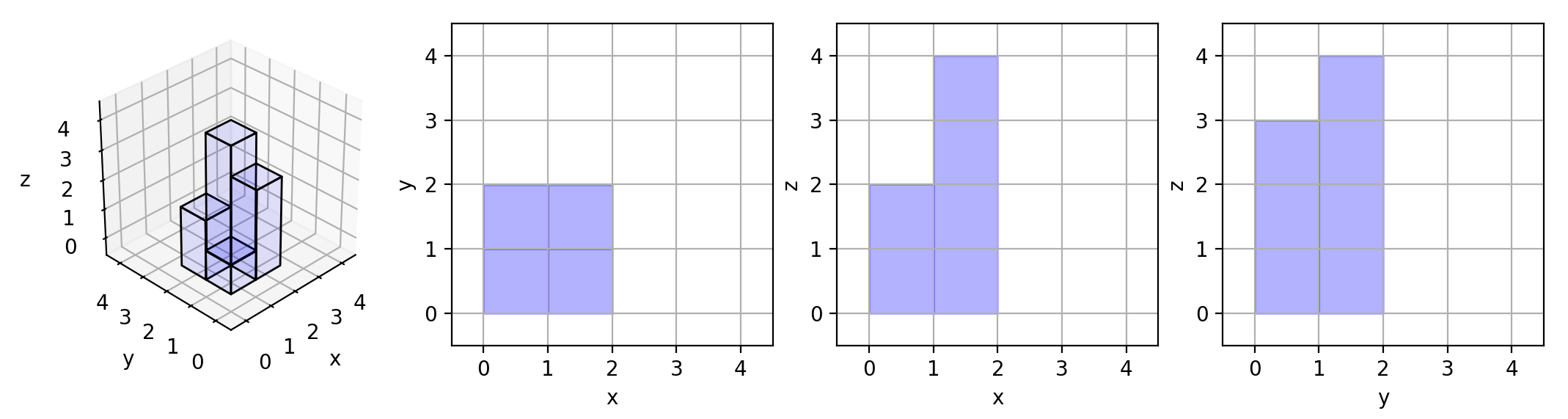
![](https://s3-lc-upload.s3.amazonaws.com/uploads/2018/08/02/shadow.png)

    
    
    Input: grid = [[1,2],[3,4]]
    Output: 17
    Explanation: Here are the three projections ("shadows") of the shape made with each axis-aligned plane.

Example 2


    
    
    Input: grid = [[2]]
    Output: 5

Example 3


    
    
    Input: grid = [[1,0],[0,2]]
    Output: 8

Constraints

  • n == grid.length == grid[i].length
  • 1 <= n <= 50
  • 0 <= grid[i][j] <= 50

Solution

Method 1 – Calculate Each Projection Separately

Intuition

The projection area is the sum of three views:

  1. Top view (xy-plane): Count of all nonzero cells.
  2. Front view (yz-plane): For each column, the maximum value.
  3. Side view (zx-plane): For each row, the maximum value.

Approach

Iterate through the grid, count nonzero cells for the top view, and keep track of row and column maximums for the side and front views.

Code

C++
class Solution {
public:
    int projectionArea(vector<vector<int>>& grid) {
        int n = grid.size(), ans = 0;
        for (int i = 0; i < n; ++i) {
            int rowMax = 0, colMax = 0;
            for (int j = 0; j < n; ++j) {
                if (grid[i][j]) ans++; // top view
                rowMax = max(rowMax, grid[i][j]);
                colMax = max(colMax, grid[j][i]);
            }
            ans += rowMax + colMax;
        }
        return ans;
    }
};
Go
func projectionArea(grid [][]int) int {
    n := len(grid)
    ans := 0
    for i := 0; i < n; i++ {
        rowMax, colMax := 0, 0
        for j := 0; j < n; j++ {
            if grid[i][j] > 0 {
                ans++
            }
            if grid[i][j] > rowMax {
                rowMax = grid[i][j]
            }
            if grid[j][i] > colMax {
                colMax = grid[j][i]
            }
        }
        ans += rowMax + colMax
    }
    return ans
}
Java
class Solution {
    public int projectionArea(int[][] grid) {
        int n = grid.length, ans = 0;
        for (int i = 0; i < n; ++i) {
            int rowMax = 0, colMax = 0;
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] > 0) ans++;
                rowMax = Math.max(rowMax, grid[i][j]);
                colMax = Math.max(colMax, grid[j][i]);
            }
            ans += rowMax + colMax;
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun projectionArea(grid: Array<IntArray>): Int {
        val n = grid.size
        var ans = 0
        for (i in 0 until n) {
            var rowMax = 0
            var colMax = 0
            for (j in 0 until n) {
                if (grid[i][j] > 0) ans++
                rowMax = maxOf(rowMax, grid[i][j])
                colMax = maxOf(colMax, grid[j][i])
            }
            ans += rowMax + colMax
        }
        return ans
    }
}
Python
from typing import List
class Solution:
    def projectionArea(self, grid: List[List[int]]) -> int:
        n = len(grid)
        ans = 0
        for i in range(n):
            row_max = col_max = 0
            for j in range(n):
                if grid[i][j] > 0:
                    ans += 1
                row_max = max(row_max, grid[i][j])
                col_max = max(col_max, grid[j][i])
            ans += row_max + col_max
        return ans
Rust
impl Solution {
    pub fn projection_area(grid: Vec<Vec<i32>>) -> i32 {
        let n = grid.len();
        let mut ans = 0;
        for i in 0..n {
            let mut row_max = 0;
            let mut col_max = 0;
            for j in 0..n {
                if grid[i][j] > 0 { ans += 1; }
                row_max = row_max.max(grid[i][j]);
                col_max = col_max.max(grid[j][i]);
            }
            ans += row_max + col_max;
        }
        ans
    }
}
TypeScript
class Solution {
    projectionArea(grid: number[][]): number {
        const n = grid.length;
        let ans = 0;
        for (let i = 0; i < n; ++i) {
            let rowMax = 0, colMax = 0;
            for (let j = 0; j < n; ++j) {
                if (grid[i][j] > 0) ans++;
                rowMax = Math.max(rowMax, grid[i][j]);
                colMax = Math.max(colMax, grid[j][i]);
            }
            ans += rowMax + colMax;
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2) where n is the size of the grid.
  • 🧺 Space complexity: O(1).

Comments