Problem

You are given a 2D integer array properties having dimensions n x m and an integer k.

Define a function intersect(a, b) that returns the number of distinct integers common to both arrays a and b.

Construct an undirected graph where each index i corresponds to properties[i]. There is an edge between node i and node j if and only if intersect(properties[i], properties[j]) >= k, where i and j are in the range [0, n - 1] and i != j.

Return the number of connected components in the resulting graph.

Examples

Example 1

1
2
3
4
5

Input: properties = [[1,2],[1,1],[3,4],[4,5],[5,6],[7,7]], k = 1
Output: 3
Explanation:
The graph formed has 3 connected components:
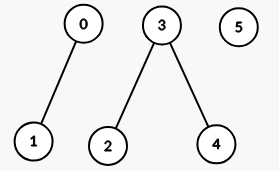
![](https://assets.leetcode.com/uploads/2025/02/27/image.png)

Example 2

1
2
3
4
5
6

Input: properties = [[1,2,3],[2,3,4],[4,3,5]], k = 2
Output: 1
Explanation:
The graph formed has 1 connected component:
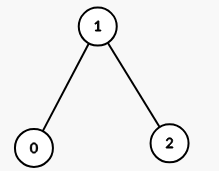
![](https://assets.leetcode.com/uploads/2025/02/27/screenshot-
from-2025-02-27-23-58-34.png)

Example 3

1
2
3
4
5
6

Input: properties = [[1,1],[1,1]], k = 2
Output: 2
Explanation:
`intersect(properties[0], properties[1]) = 1`, which is less than `k`. This
means there is no edge between `properties[0]` and `properties[1]` in the
graph.

Constraints

  • 1 <= n == properties.length <= 100
  • 1 <= m == properties[i].length <= 100
  • 1 <= properties[i][j] <= 100
  • 1 <= k <= m

Solution

Method 1 – Build Graph and Count Connected Components (DFS/Union-Find)

Intuition

We can model the problem as a graph where each node is a property, and an edge exists if two properties share at least k distinct integers. The number of connected components can be found using DFS or Union-Find.

Approach

  1. For each pair (i, j), compute the number of distinct integers in common between properties[i] and properties[j].
  2. If the intersection is at least k, add an undirected edge between i and j.
  3. Use DFS or Union-Find to count the number of connected components in the graph.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

#include <vector>
#include <unordered_set>
using namespace std;
class Solution {
public:
    int countComponents(vector<vector<int>>& properties, int k) {
        int n = properties.size();
        vector<vector<int>> graph(n);
        for (int i = 0; i < n; ++i) {
            unordered_set<int> seti(properties[i].begin(), properties[i].end());
            for (int j = i+1; j < n; ++j) {
                unordered_set<int> setj(properties[j].begin(), properties[j].end());
                int cnt = 0;
                for (int x : seti) if (setj.count(x)) ++cnt;
                if (cnt >= k) {
                    graph[i].push_back(j);
                    graph[j].push_back(i);
                }
            }
        }
        vector<bool> vis(n);
        int ans = 0;
        function<void(int)> dfs = [&](int u) {
            vis[u] = true;
            for (int v : graph[u]) if (!vis[v]) dfs(v);
        };
        for (int i = 0; i < n; ++i) if (!vis[i]) { ++ans; dfs(i); }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

func countComponents(properties [][]int, k int) int {
    n := len(properties)
    graph := make([][]int, n)
    for i := 0; i < n; i++ {
        seti := map[int]struct{}{}
        for _, x := range properties[i] { seti[x] = struct{}{} }
        for j := i+1; j < n; j++ {
            setj := map[int]struct{}{}
            for _, x := range properties[j] { setj[x] = struct{}{} }
            cnt := 0
            for x := range seti { if _, ok := setj[x]; ok { cnt++ } }
            if cnt >= k {
                graph[i] = append(graph[i], j)
                graph[j] = append(graph[j], i)
            }
        }
    }
    vis := make([]bool, n)
    var dfs func(int)
    dfs = func(u int) {
        vis[u] = true
        for _, v := range graph[u] {
            if !vis[v] { dfs(v) }
        }
    }
    ans := 0
    for i := 0; i < n; i++ {
        if !vis[i] { ans++; dfs(i) }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

import java.util.*;
class Solution {
    public int countComponents(int[][] properties, int k) {
        int n = properties.length;
        List<List<Integer>> graph = new ArrayList<>();
        for (int i = 0; i < n; ++i) graph.add(new ArrayList<>());
        for (int i = 0; i < n; ++i) {
            Set<Integer> seti = new HashSet<>();
            for (int x : properties[i]) seti.add(x);
            for (int j = i+1; j < n; ++j) {
                Set<Integer> setj = new HashSet<>();
                for (int x : properties[j]) setj.add(x);
                int cnt = 0;
                for (int x : seti) if (setj.contains(x)) cnt++;
                if (cnt >= k) {
                    graph.get(i).add(j);
                    graph.get(j).add(i);
                }
            }
        }
        boolean[] vis = new boolean[n];
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            if (!vis[i]) {
                ans++;
                dfs(i, graph, vis);
            }
        }
        return ans;
    }
    private void dfs(int u, List<List<Integer>> graph, boolean[] vis) {
        vis[u] = true;
        for (int v : graph.get(u)) if (!vis[v]) dfs(v, graph, vis);
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    fun countComponents(properties: Array<IntArray>, k: Int): Int {
        val n = properties.size
        val graph = Array(n) { mutableListOf<Int>() }
        for (i in 0 until n) {
            val seti = properties[i].toSet()
            for (j in i+1 until n) {
                val setj = properties[j].toSet()
                val cnt = seti.intersect(setj).size
                if (cnt >= k) {
                    graph[i].add(j)
                    graph[j].add(i)
                }
            }
        }
        val vis = BooleanArray(n)
        fun dfs(u: Int) {
            vis[u] = true
            for (v in graph[u]) if (!vis[v]) dfs(v)
        }
        var ans = 0
        for (i in 0 until n) {
            if (!vis[i]) { ans++; dfs(i) }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

from typing import List
class Solution:
    def countComponents(self, properties: List[List[int]], k: int) -> int:
        n = len(properties)
        graph = [[] for _ in range(n)]
        sets = [set(row) for row in properties]
        for i in range(n):
            for j in range(i+1, n):
                if len(sets[i] & sets[j]) >= k:
                    graph[i].append(j)
                    graph[j].append(i)
        vis = [False] * n
        def dfs(u):
            vis[u] = True
            for v in graph[u]:
                if not vis[v]:
                    dfs(v)
        ans = 0
        for i in range(n):
            if not vis[i]:
                ans += 1
                dfs(i)
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

use std::collections::HashSet;
impl Solution {
    pub fn count_components(properties: Vec<Vec<i32>>, k: i32) -> i32 {
        let n = properties.len();
        let sets: Vec<HashSet<i32>> = properties.iter().map(|row| row.iter().cloned().collect()).collect();
        let mut graph = vec![vec![]; n];
        for i in 0..n {
            for j in (i+1)..n {
                if sets[i].intersection(&sets[j]).count() as i32 >= k {
                    graph[i].push(j);
                    graph[j].push(i);
                }
            }
        }
        let mut vis = vec![false; n];
        fn dfs(u: usize, graph: &Vec<Vec<usize>>, vis: &mut Vec<bool>) {
            vis[u] = true;
            for &v in &graph[u] {
                if !vis[v] { dfs(v, graph, vis); }
            }
        }
        let mut ans = 0;
        for i in 0..n {
            if !vis[i] { ans += 1; dfs(i, &graph, &mut vis); }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    countComponents(properties: number[][], k: number): number {
        const n = properties.length;
        const sets = properties.map(row => new Set(row));
        const graph: number[][] = Array.from({length: n}, () => []);
        for (let i = 0; i < n; ++i) {
            for (let j = i+1; j < n; ++j) {
                let cnt = 0;
                for (const x of sets[i]) if (sets[j].has(x)) cnt++;
                if (cnt >= k) {
                    graph[i].push(j);
                    graph[j].push(i);
                }
            }
        }
        const vis = Array(n).fill(false);
        function dfs(u: number) {
            vis[u] = true;
            for (const v of graph[u]) if (!vis[v]) dfs(v);
        }
        let ans = 0;
        for (let i = 0; i < n; ++i) {
            if (!vis[i]) { ans++; dfs(i); }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^2 * m), where n is the number of properties and m is the number of elements in each property. For each pair, we compute intersection in O(m).
  • 🧺 Space complexity: O(n * m) for storing sets and the adjacency list.