Problem

You are given two arrays of positive integers, boxes and warehouse, representing the heights of some boxes of unit width and the heights of n rooms in a warehouse respectively. The warehouse’s rooms are labeled from 0 to n - 1 from left to right where warehouse[i] (0-indexed) is the height of the ith room.

Boxes are put into the warehouse by the following rules:

  • Boxes cannot be stacked.
  • You can rearrange the insertion order of the boxes.
  • Boxes can be pushed into the warehouse from either side (left or right)
  • If the height of some room in the warehouse is less than the height of a box, then that box and all other boxes behind it will be stopped before that room.

Return the maximum number of boxes you can put into the warehouse.

Examples

Example 1:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1500-1599/1580.Put%20Boxes%20Into%20the%20Warehouse%20II/images/22.png)
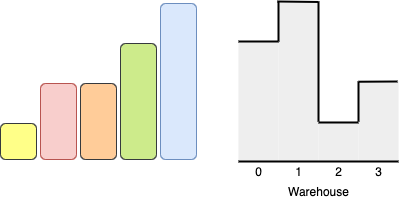
Input: boxes = [1,2,2,3,4], warehouse = [3,4,1,2]
Output: 4
Explanation:
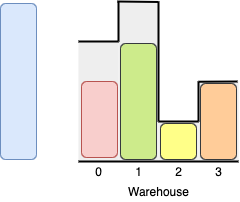
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1500-1599/1580.Put%20Boxes%20Into%20the%20Warehouse%20II/images/22-1.png)
We can store the boxes in the following order:
1- Put the yellow box in room 2 from either the left or right side.
2- Put the orange box in room 3 from the right side.
3- Put the green box in room 1 from the left side.
4- Put the red box in room 0 from the left side.
Notice that there are other valid ways to put 4 boxes such as swapping the red and green boxes or the red and orange boxes.

Example 2:

1
2
3
4
5
6
7

![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1500-1599/1580.Put%20Boxes%20Into%20the%20Warehouse%20II/images/22-2.png)
Input: boxes = [3,5,5,2], warehouse = [2,1,3,4,5]
Output: 3
Explanation:
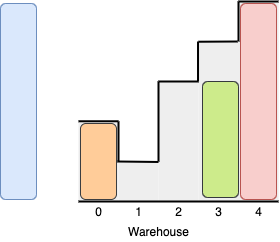
![](https://fastly.jsdelivr.net/gh/doocs/leetcode@main/solution/1500-1599/1580.Put%20Boxes%20Into%20the%20Warehouse%20II/images/22-3.png)
It is not possible to put the two boxes of height 5 in the warehouse since there's only 1 room of height >= 5.
Other valid solutions are to put the green box in room 2 or to put the orange box first in room 2 before putting the green and red boxes.

Constraints:

  • n == warehouse.length
  • 1 <= boxes.length, warehouse.length <= 10^5
  • 1 <= boxes[i], warehouse[i] <= 10^9

Solution

Method 1 – Two Pointers and Greedy

Intuition

Since boxes can be inserted from either side, we can always choose the best fit for each room from both ends. By sorting the boxes and using two pointers for the warehouse, we can maximize the number of boxes placed.

Approach

  1. Sort the boxes in ascending order.
  2. Use two pointers (l and r) for the left and right ends of the warehouse.
  3. For each box (from smallest to largest), try to fit it into the leftmost or rightmost available room (whichever can fit it and is more restrictive).
  4. Move the pointer inward after placing a box, and continue until all boxes or rooms are used.
  5. Return the total number of boxes placed.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

class Solution {
public:
    int maxBoxesInWarehouse(vector<int>& boxes, vector<int>& warehouse) {
        sort(boxes.begin(), boxes.end());
        int l = 0, r = warehouse.size() - 1, i = 0, j = boxes.size() - 1, ans = 0;
        while (i <= j && l <= r) {
            if (warehouse[l] < warehouse[r]) {
                if (boxes[i] <= warehouse[l]) { ++ans; ++i; }
                ++l;
            } else {
                if (boxes[i] <= warehouse[r]) { ++ans; ++i; }
                --r;
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

func maxBoxesInWarehouse(boxes []int, warehouse []int) int {
    sort.Ints(boxes)
    l, r := 0, len(warehouse)-1
    i, ans := 0, 0
    for i < len(boxes) && l <= r {
        if warehouse[l] < warehouse[r] {
            if boxes[i] <= warehouse[l] { ans++; i++ }
            l++
        } else {
            if boxes[i] <= warehouse[r] { ans++; i++ }
            r--
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    public int maxBoxesInWarehouse(int[] boxes, int[] warehouse) {
        Arrays.sort(boxes);
        int l = 0, r = warehouse.length - 1, i = 0, ans = 0;
        while (i < boxes.length && l <= r) {
            if (warehouse[l] < warehouse[r]) {
                if (boxes[i] <= warehouse[l]) { ans++; i++; }
                l++;
            } else {
                if (boxes[i] <= warehouse[r]) { ans++; i++; }
                r--;
            }
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    fun maxBoxesInWarehouse(boxes: IntArray, warehouse: IntArray): Int {
        boxes.sort()
        var l = 0; var r = warehouse.size - 1; var i = 0; var ans = 0
        while (i < boxes.size && l <= r) {
            if (warehouse[l] < warehouse[r]) {
                if (boxes[i] <= warehouse[l]) { ans++; i++ }
                l++
            } else {
                if (boxes[i] <= warehouse[r]) { ans++; i++ }
                r--
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

from typing import List
class Solution:
    def maxBoxesInWarehouse(self, boxes: List[int], warehouse: List[int]) -> int:
        boxes.sort()
        l, r = 0, len(warehouse) - 1
        i, ans = 0, 0
        while i < len(boxes) and l <= r:
            if warehouse[l] < warehouse[r]:
                if boxes[i] <= warehouse[l]:
                    ans += 1
                    i += 1
                l += 1
            else:
                if boxes[i] <= warehouse[r]:
                    ans += 1
                    i += 1
                r -= 1
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

impl Solution {
    pub fn max_boxes_in_warehouse(mut boxes: Vec<i32>, warehouse: Vec<i32>) -> i32 {
        boxes.sort();
        let (mut l, mut r, mut i, mut ans) = (0, warehouse.len()-1, 0, 0);
        while i < boxes.len() && l <= r {
            if warehouse[l] < warehouse[r] {
                if boxes[i] <= warehouse[l] { ans += 1; i += 1; }
                l += 1;
            } else {
                if boxes[i] <= warehouse[r] { ans += 1; i += 1; }
                if r == 0 { break; }
                r -= 1;
            }
        }
        ans as i32
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

class Solution {
    maxBoxesInWarehouse(boxes: number[], warehouse: number[]): number {
        boxes.sort((a, b) => a - b);
        let l = 0, r = warehouse.length - 1, i = 0, ans = 0;
        while (i < boxes.length && l <= r) {
            if (warehouse[l] < warehouse[r]) {
                if (boxes[i] <= warehouse[l]) { ans++; i++; }
                l++;
            } else {
                if (boxes[i] <= warehouse[r]) { ans++; i++; }
                r--;
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(N log N + M), where N is the number of boxes and M is the number of warehouse rooms. Sorting boxes is O(N log N), and the two-pointer scan is O(M).
  • 🧺 Space complexity: O(1), ignoring the space for sorting.