Pyramid Transition Matrix
Problem
You are stacking blocks to form a pyramid. Each block has a color, which is represented by a single letter. Each row of blocks contains one less block than the row beneath it and is centered on top.
To make the pyramid aesthetically pleasing, there are only specific
triangular patterns that are allowed. A triangular pattern consists of a
single block stacked on top of two blocks. The patterns are given as a list of three-letter strings allowed, where the first two characters of a pattern represent the left and right bottom blocks respectively, and the third character is the top block.
- For example,
"ABC"represents a triangular pattern with a'C'block stacked on top of an'A'(left) and'B'(right) block. Note that this is different from"BAC"where'B'is on the left bottom and'A'is on the right bottom.
You start with a bottom row of blocks bottom, given as a single string, that you must use as the base of the pyramid.
Given bottom and allowed, return true _if you can build the pyramid all the way to the top such thatevery triangular pattern in the pyramid is in _allowed , orfalse otherwise.
Examples
Example 1
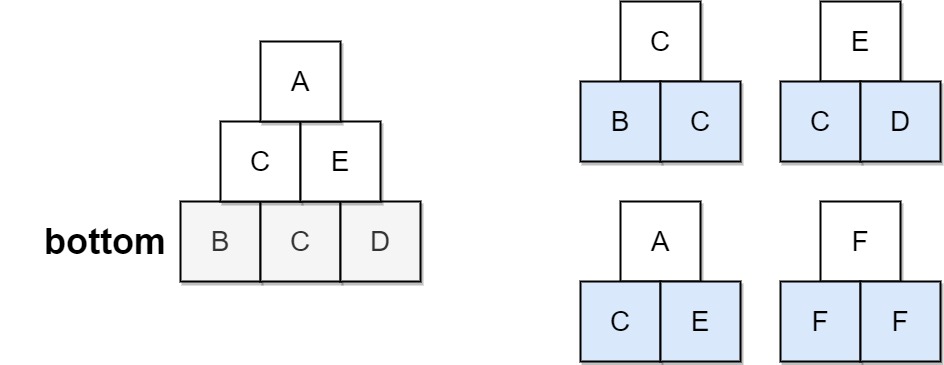
Input: bottom = "BCD", allowed = ["BCC","CDE","CEA","FFF"]
Output: true
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 3), we can build "CE" on level 2 and then build "A" on level 1.
There are three triangular patterns in the pyramid, which are "BCC", "CDE", and "CEA". All are allowed.
Example 2
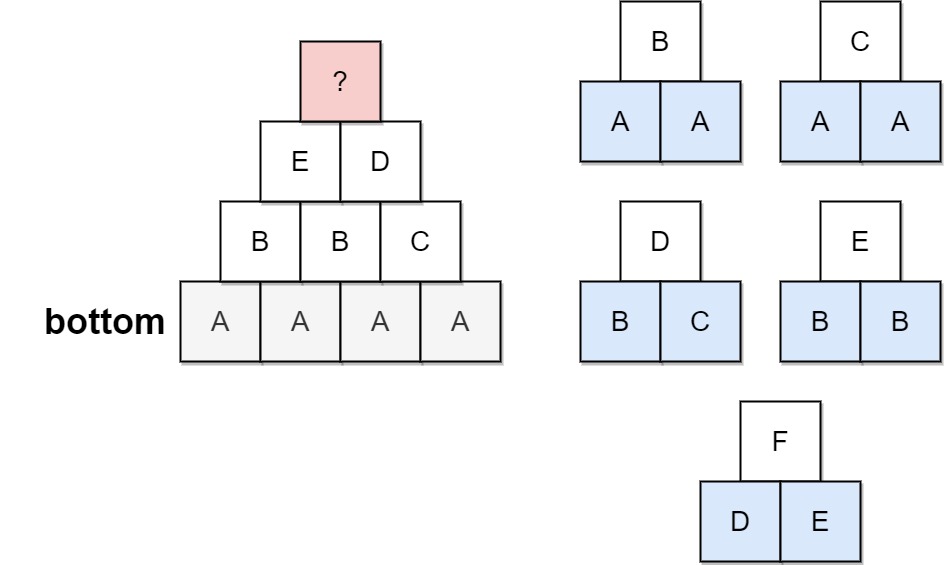
Input: bottom = "AAAA", allowed = ["AAB","AAC","BCD","BBE","DEF"]
Output: false
Explanation: The allowed triangular patterns are shown on the right.
Starting from the bottom (level 4), there are multiple ways to build level 3, but trying all the possibilites, you will get always stuck before building level 1.
Constraints
2 <= bottom.length <= 60 <= allowed.length <= 216allowed[i].length == 3- The letters in all input strings are from the set
{'A', 'B', 'C', 'D', 'E', 'F'}. - All the values of
allowedare unique.
Solution
Method 1 – DFS with Backtracking
Intuition
We can recursively try to build the pyramid from the bottom up, trying all possible valid blocks for each position using the allowed patterns. If we reach the top, we succeed; if we get stuck, we backtrack.
Approach
- Build a mapping from each pair of blocks to all possible top blocks using the allowed patterns.
- Use DFS to try all possible next rows, recursively building up the pyramid.
- For each level, for every adjacent pair, try all possible top blocks and proceed recursively.
- If we reach a row of length 1, return true. If no valid build is possible, return false.
Code
C++
class Solution {
public:
bool pyramidTransition(string bottom, vector<string>& allowed) {
unordered_map<string, vector<char>> mp;
for (auto& s : allowed) mp[s.substr(0,2)].push_back(s[2]);
return dfs(bottom, mp);
}
bool dfs(string row, unordered_map<string, vector<char>>& mp) {
if (row.size() == 1) return true;
vector<string> nexts = {""};
for (int i = 0; i < row.size()-1; ++i) {
string key = row.substr(i,2);
if (!mp.count(key)) return false;
vector<string> tmp;
for (auto& pre : nexts)
for (char c : mp[key]) tmp.push_back(pre + c);
nexts = tmp;
}
for (auto& n : nexts)
if (dfs(n, mp)) return true;
return false;
}
};
Go
func pyramidTransition(bottom string, allowed []string) bool {
mp := map[string][]byte{}
for _, s := range allowed {
k := s[:2]
mp[k] = append(mp[k], s[2])
}
var dfs func(string) bool
dfs = func(row string) bool {
if len(row) == 1 { return true }
nexts := []string{""}
for i := 0; i < len(row)-1; i++ {
k := row[i:i+2]
vs, ok := mp[k]
if !ok { return false }
tmp := []string{}
for _, pre := range nexts {
for _, c := range vs {
tmp = append(tmp, pre+string(c))
}
}
nexts = tmp
}
for _, n := range nexts {
if dfs(n) { return true }
}
return false
}
return dfs(bottom)
}
Java
class Solution {
public boolean pyramidTransition(String bottom, List<String> allowed) {
Map<String, List<Character>> mp = new HashMap<>();
for (String s : allowed) mp.computeIfAbsent(s.substring(0,2), k -> new ArrayList<>()).add(s.charAt(2));
return dfs(bottom, mp);
}
private boolean dfs(String row, Map<String, List<Character>> mp) {
if (row.length() == 1) return true;
List<String> nexts = new ArrayList<>(); nexts.add("");
for (int i = 0; i < row.length()-1; ++i) {
String key = row.substring(i,i+2);
if (!mp.containsKey(key)) return false;
List<String> tmp = new ArrayList<>();
for (String pre : nexts)
for (char c : mp.get(key)) tmp.add(pre + c);
nexts = tmp;
}
for (String n : nexts)
if (dfs(n, mp)) return true;
return false;
}
}
Kotlin
class Solution {
fun pyramidTransition(bottom: String, allowed: List<String>): Boolean {
val mp = mutableMapOf<String, MutableList<Char>>()
for (s in allowed) mp.getOrPut(s.substring(0,2)) { mutableListOf() }.add(s[2])
fun dfs(row: String): Boolean {
if (row.length == 1) return true
var nexts = listOf("")
for (i in 0 until row.length-1) {
val key = row.substring(i,i+2)
val vs = mp[key] ?: return false
val tmp = mutableListOf<String>()
for (pre in nexts)
for (c in vs) tmp.add(pre + c)
nexts = tmp
}
for (n in nexts) if (dfs(n)) return true
return false
}
return dfs(bottom)
}
}
Python
from typing import List
class Solution:
def pyramidTransition(self, bottom: str, allowed: List[str]) -> bool:
from collections import defaultdict
mp = defaultdict(list)
for s in allowed:
mp[s[:2]].append(s[2])
def dfs(row: str) -> bool:
if len(row) == 1:
return True
nexts = ['']
for i in range(len(row)-1):
key = row[i:i+2]
if key not in mp:
return False
tmp = []
for pre in nexts:
for c in mp[key]:
tmp.append(pre + c)
nexts = tmp
for n in nexts:
if dfs(n):
return True
return False
return dfs(bottom)
Rust
use std::collections::HashMap;
impl Solution {
pub fn pyramid_transition(bottom: String, allowed: Vec<String>) -> bool {
let mut mp: HashMap<&str, Vec<char>> = HashMap::new();
for s in &allowed {
mp.entry(&s[0..2]).or_default().push(s.chars().nth(2).unwrap());
}
fn dfs(row: &str, mp: &HashMap<&str, Vec<char>>) -> bool {
if row.len() == 1 { return true; }
let mut nexts = vec![String::new()];
for i in 0..row.len()-1 {
let key = &row[i..i+2];
let vs = match mp.get(key) { Some(v) => v, None => return false };
let mut tmp = vec![];
for pre in &nexts {
for &c in vs {
let mut s = pre.clone();
s.push(c);
tmp.push(s);
}
}
nexts = tmp;
}
for n in &nexts {
if dfs(n, mp) { return true; }
}
false
}
dfs(&bottom, &mp)
}
}
TypeScript
class Solution {
pyramidTransition(bottom: string, allowed: string[]): boolean {
const mp: Record<string, string[]> = {};
for (const s of allowed) {
if (!mp[s.slice(0,2)]) mp[s.slice(0,2)] = [];
mp[s.slice(0,2)].push(s[2]);
}
function dfs(row: string): boolean {
if (row.length === 1) return true;
let nexts = [''];
for (let i = 0; i < row.length-1; ++i) {
const key = row.slice(i,i+2);
if (!mp[key]) return false;
const tmp: string[] = [];
for (const pre of nexts)
for (const c of mp[key]) tmp.push(pre + c);
nexts = tmp;
}
for (const n of nexts) if (dfs(n)) return true;
return false;
}
return dfs(bottom);
}
}
Complexity
- ⏰ Time complexity:
O(k^n), where n is the length of the bottom and k is the average number of allowed blocks per pair. The search space is exponential in the height of the pyramid. - 🧺 Space complexity:
O(n), for the recursion stack.