problemmediumalgorithmsleetcode-1828leetcode 1828leetcode1828

Queries on Number of Points Inside a Circle

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an array points where points[i] = [xi, yi] is the coordinates of the ith point on a 2D plane. Multiple points can have the same coordinates.

You are also given an array queries where queries[j] = [xj, yj, rj] describes a circle centered at (xj, yj) with a radius of rj.

For each query queries[j], compute the number of points inside the jth circle. Points on the border of the circle are considered inside.

Return an arrayanswer , whereanswer[j]is the answer to thejth query.

Examples

Example 1


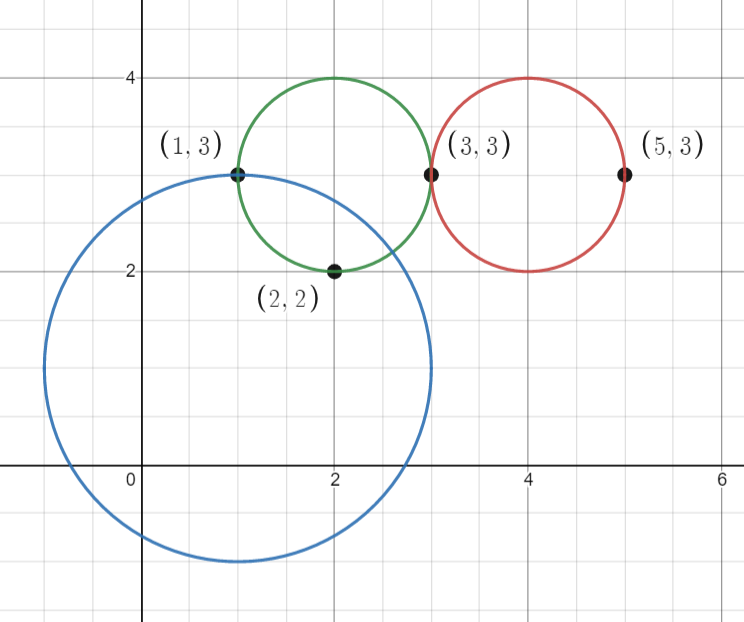
![](https://assets.leetcode.com/uploads/2021/03/25/chrome_2021-03-25_22-34-16.png)

Input: points = [[1,3],[3,3],[5,3],[2,2]], queries = [[2,3,1],[4,3,1],[1,1,2]]
Output: [3,2,2]
Explanation: The points and circles are shown above.
queries[0] is the green circle, queries[1] is the red circle, and queries[2] is the blue circle.

Example 2


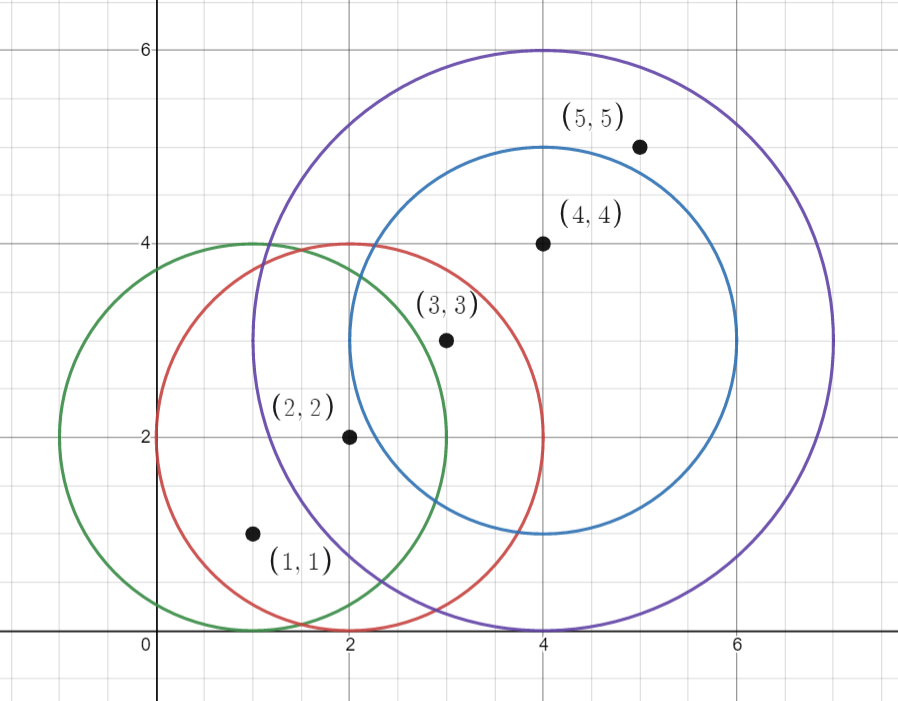
![](https://assets.leetcode.com/uploads/2021/03/25/chrome_2021-03-25_22-42-07.png)

Input: points = [[1,1],[2,2],[3,3],[4,4],[5,5]], queries = [[1,2,2],[2,2,2],[4,3,2],[4,3,3]]
Output: [2,3,2,4]
Explanation: The points and circles are shown above.
queries[0] is green, queries[1] is red, queries[2] is blue, and queries[3] is purple.

Constraints

  • 1 <= points.length <= 500
  • points[i].length == 2
  • 0 <= x​​​​​​i, y​​​​​​i <= 500
  • 1 <= queries.length <= 500
  • queries[j].length == 3
  • 0 <= xj, yj <= 500
  • 1 <= rj <= 500
  • All coordinates are integers.

Follow up: Could you find the answer for each query in better complexity than O(n)?

Solution

Method 1 – Brute Force Distance Check

Intuition

For each query, check every point to see if it lies inside or on the border of the circle using the distance formula. This is efficient enough for the given constraints.

Approach

  1. For each query [xj, yj, rj], iterate through all points.
  2. For each point [xi, yi], check if (xi - xj)^2 + (yi - yj)^2 <= rj^2.
  3. Count the number of points that satisfy the condition for each query.
  4. Return the result for all queries.

Code

C++
class Solution {
public:
    vector<int> countPoints(vector<vector<int>>& points, vector<vector<int>>& queries) {
        vector<int> ans;
        for (auto& q : queries) {
            int cnt = 0, x = q[0], y = q[1], r2 = q[2] * q[2];
            for (auto& p : points) {
                int dx = p[0] - x, dy = p[1] - y;
                if (dx*dx + dy*dy <= r2) ++cnt;
            }
            ans.push_back(cnt);
        }
        return ans;
    }
};
Go
func countPoints(points [][]int, queries [][]int) []int {
    ans := make([]int, len(queries))
    for i, q := range queries {
        x, y, r2 := q[0], q[1], q[2]*q[2]
        cnt := 0
        for _, p := range points {
            dx, dy := p[0]-x, p[1]-y
            if dx*dx+dy*dy <= r2 {
                cnt++
            }
        }
        ans[i] = cnt
    }
    return ans
}
Java
class Solution {
    public int[] countPoints(int[][] points, int[][] queries) {
        int[] ans = new int[queries.length];
        for (int i = 0; i < queries.length; ++i) {
            int x = queries[i][0], y = queries[i][1], r2 = queries[i][2] * queries[i][2];
            int cnt = 0;
            for (int[] p : points) {
                int dx = p[0] - x, dy = p[1] - y;
                if (dx*dx + dy*dy <= r2) ++cnt;
            }
            ans[i] = cnt;
        }
        return ans;
    }
}
Kotlin
class Solution {
    fun countPoints(points: Array<IntArray>, queries: Array<IntArray>): IntArray {
        return queries.map { (x, y, r) ->
            points.count { (px, py) -> (px - x) * (px - x) + (py - y) * (py - y) <= r * r }
        }.toIntArray()
    }
}
Python
from typing import List
class Solution:
    def countPoints(self, points: List[List[int]], queries: List[List[int]]) -> List[int]:
        ans = []
        for x, y, r in queries:
            cnt = 0
            for xi, yi in points:
                if (xi - x) ** 2 + (yi - y) ** 2 <= r * r:
                    cnt += 1
            ans.append(cnt)
        return ans
Rust
impl Solution {
    pub fn count_points(points: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {
        queries.iter().map(|q| {
            let (x, y, r2) = (q[0], q[1], q[2]*q[2]);
            points.iter().filter(|p| {
                let dx = p[0] - x;
                let dy = p[1] - y;
                dx*dx + dy*dy <= r2
            }).count() as i32
        }).collect()
    }
}
TypeScript
class Solution {
    countPoints(points: number[][], queries: number[][]): number[] {
        return queries.map(([x, y, r]) =>
            points.filter(([px, py]) => (px - x) ** 2 + (py - y) ** 2 <= r * r).length
        );
    }
}

Complexity

  • ⏰ Time complexity: O(Q * N), where Q is the number of queries and N is the number of points. Each query checks all points.
  • 🧺 Space complexity: O(1), not counting the output array.

Comments