Rabin-Karp Algorithm Explained
Introduction
This is part of [Find the Index of the First Occurrence in a String](find-the-index-of-the-first-occurrence-in-a-string).
The Rabin-Karp Algorithm, created by Richard M. Karp and Michael O. Rabin in 1987, is a string searching technique that uses hashing to locate any one of a set of pattern strings within a text.
Like the Naive Algorithm, the Rabin-Karp algorithm slides the pattern over the text one character at a time. However, unlike the Naive algorithm, the Rabin-Karp algorithm first compares the hash value of the pattern with the hash value of the current substring in the text. If the hash values match, it then proceeds to match the characters individually. Thus, the Rabin-Karp algorithm computes hash values for the following:
- The pattern itself.
- All substrings of the text with length equal to the pattern.
To efficiently compute hash values for all substrings of the text of size m, a suitable hash function is essential.
The concept is straightforward, but it requires a hash function that provides unique hashes for different substrings. Such a hash function can use ASCII codes for characters, but care must be taken to ensure it supports multiple languages.
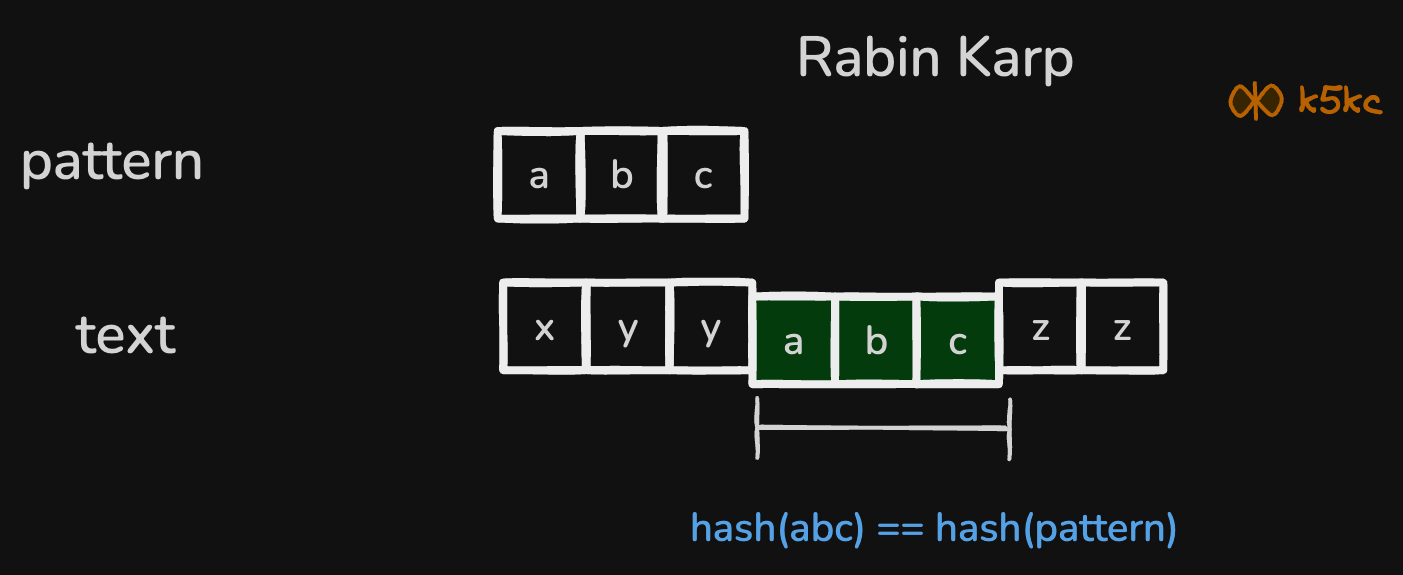
The hash function can be based on various criteria, such as converting ASCII characters to numbers or other methods. The main requirement is to convert a string (pattern) into a hash that is quicker to compare. For example, consider the string "hello world" with a hash value of hash('hello world') = 12345. If hash('he') = 1, it indicates that the pattern "he" is present in the text "hello world". At each step, we extract a substring from the text with the same length as the pattern, compute its hash, and directly compare it to the pattern's hash, as demonstrated in the image.
Understanding Hash functions
[Calculate Hash Code for String](calculate-hash-code-for-string)
Algorithm without rolling hash
Now lets use use [|string hash calculation](calculate-hash-code-for-string) to write simple rabin karp algorithm without rolling hash. In this basic example, we will use a simple hash function to convert characters into integers and then calculate the hash values for the pattern and the text's substrin
Code
Java
public class Solution {
// Function to create a hash table and compute hash value
private int hashString(String str, int len) {
Map<Character, Integer> hashTable = new HashMap<>();
hashTable.put('h', 1);
hashTable.put('e', 2);
hashTable.put('l', 3);
hashTable.put('o', 4);
hashTable.put('w', 5);
hashTable.put('r', 6);
hashTable.put('d', 7);
int hash = 0;
for (int i = 0; i < len; i++) {
hash = hash * 10 + hashTable.getOrDefault(str.charAt(i), 0);
}
return hash;
}
public int rabinKarp(String text, String pattern) {
int n = text.length();
int m = pattern.length();
if (m > n) {
return -1;
}
int patternHash = hashString(pattern, m);
int textHash = hashString(text.substring(0, m), m);
for (int i = 0; i <= n - m; i++) {
if (patternHash == textHash) {
if (text.substring(i, i + m).equals(pattern)) {
return i;
}
}
if (i < n - m) {
textHash = hashString(text.substring(i + 1, i + 1 + m), m);
}
}
return -1;
}
}
Python
class Solution:
def __init__(self):
self.hash_table = {
'h': 1,
'e': 2,
'l': 3,
'o': 4,
'w': 5,
'r': 6,
'd': 7
}
def hash_string(self, s: str, length: int) -> int:
h = 0
for i in range(length):
h = h * 10 + self.hash_table.get(s[i], 0)
return h
def rabin_karp(self, text: str, pattern: str) -> int:
n = len(text)
m = len(pattern)
if m > n:
return -1
pattern_hash = self.hash_string(pattern, m)
text_hash = self.hash_string(text[:m], m)
for i in range(n - m + 1):
if pattern_hash == text_hash:
if text[i:i + m] == pattern:
return i
if i < n - m:
text_hash = self.hash_string(text[i + 1:i + 1 + m], m)
return -1
Complexity
- ⏰ Time complexity:
O(m * n), wherenis the length of the text andmis the length of the pattern. This is due to the repeated calculation of the hash for each substring. - 🧺 Space complexity:
O(1), as the extra space used does not depend on the input size.
Follow up
Lets see if we can improve the algorithm further using Rabin Karp - [#Algorithm with Rolling Hash](#algorithm-with-rolling-hash).
Calculate Rolling hash
[Calculate Rolling Hashcode for String](calculate-rolling-hashcode-for-string)
Algorithm with Rolling Hash
We have already discussed some part of the problem here: [#Algorithm without rolling hash](#algorithm-without-rolling-hash). The main drawback of the previous solution was having to recalculate the hash for each substring. This led to time complexity similar to the naive approach.
In this section, we will discuss a more efficient solution using rolling hashes. Before that read - [Calculate Rolling Hashcode for String](calculate-rolling-hashcode-for-string).
Rabin fingerprint is an implementation of a rolling hash algorithm.
Code
Java
To see how it works lets look at an example:
public int strStr(String haystack, String needle) {
RabinKarp rk = new RabinKarp(needle);
return rk.search(haystack);
}
public class RabinKarp {
private final String pat; // pattern to search for
private final long patHash; // hash value of the pattern
private final int m; // length of the pattern
private static final long R = 256; // radix
private static final long Q = (long) 1e9 + 7; // large prime for modulus to avoid overflow
private final long windowPower; // R^(m-1) % Q
public RabinKarp(String pat) {
this.pat = pat;
this.m = pat.length();
this.patHash = hash(this.pat);
// precompute R^(m-1) % Q for use in removing leading digit
long temp = 1;
for (int i = 1; i <= m - 1; i++) {
temp = (R * temp) % Q;
}
windowPower = temp;
}
// Hash function for a string
private long hash(String s) {
long h = 0;
for (int i = 0; i < s.length(); i++) {
h = (h * R + s.charAt(i)) % Q;
}
return h;
}
// Compute next hash value for the rolling hash
private long getNextHash(long currHash, char prevCh, char currCh) {
long nextHash = currHash;
nextHash = (nextHash + Q - (windowPower * prevCh) % Q) % Q;
nextHash = (nextHash * R + currCh) % Q;
return nextHash;
}
// Check if the pattern matches the text starting from index i
private boolean check(String txt, int i) {
for (int j = 0; j < m; j++) {
if (pat.charAt(j) != txt.charAt(i + j)) {
return false;
}
}
return true;
}
// Search for the pattern in the given text
public int search(String txt) {
int n = txt.length();
if (n < m) {
return -1;
}
long txtHash = hash(txt.substring(0, m));
// Check for match at offset 0
if ((patHash == txtHash) && check(txt, 0)) {
return 0;
}
// Check for hash match; if hash match, confirm with exact match
int j = m - 1;
for (int i = 1; i <= n - m; i++) {
txtHash = getNextHash(txtHash, txt.charAt(i - 1), txt.charAt(i + j));
if ((patHash == txtHash) && check(txt, i)) {
return i;
}
}
// No match found
return -1;
}
}
Python
class RabinKarp:
R = 256 # radix
Q = int(1e9 + 7) # large prime for modulus to avoid overflow
def __init__(self, pat: str):
self.pat = pat
self.m = len(pat)
self.patHash = self.hash(pat)
self.windowPower = self.compute_window_power()
def compute_window_power(self):
temp = 1
for i in range(1, self.m):
temp = (RabinKarp.R * temp) % RabinKarp.Q
return temp
def hash(self, s: str):
h = 0
for char in s:
h = (h * RabinKarp.R + ord(char)) % RabinKarp.Q
return h
def get_next_hash(self, curr_hash, prev_ch, curr_ch):
next_hash = curr_hash
next_hash = (next_hash + RabinKarp.Q - (self.windowPower * ord(prev_ch)) % RabinKarp.Q) % RabinKarp.Q
next_hash = (next_hash * RabinKarp.R + ord(curr_ch)) % RabinKarp.Q
return next_hash
def check(self, txt: str, i: int):
for j in range(self.m):
if self.pat[j] != txt[i + j]:
return False
return True
def search(self, txt: str):
n = len(txt)
if n < self.m:
return -1
txtHash = self.hash(txt[:self.m])
# Check for match at offset 0
if self.patHash == txtHash and self.check(txt, 0):
return 0
# Check for hash match; if hash match, confirm with exact match
for i in range(1, n - self.m + 1):
txtHash = self.get_next_hash(txtHash, txt[i - 1], txt[i + self.m - 1])
if self.patHash == txtHash and self.check(txt, i):
return i
# No match found
return -1
# Example usage
rk = RabinKarp("needle")
print(rk.search("haystack with a needle inside")) # Output will be the starting index of "needle" in the haystack string
Complexity
Time Complexity
Average case: O(n + m)
Worst case: O(n * m)
The average and best-case running time of the Rabin-Karp algorithm is O(n + m), but the worst-case time is O(n * m). This is because the algorithm could find a false positive for each of the n positions, and it requires up to m comparisons to verify the match.
With a reasonably good hash function, such false positives are unlikely to occur often. However, it is theoretically possible to construct a query where false positives cause worst-case performance.
Therefore, while Rabin-Karp has an expected time complexity of O(n), its worst-case time complexity remains O(n * m). Since m is typically less than or equal to n, O(n + m) is fundamentally the same as O(n).
Space Complexity
Space Complexity: O(m), where m is the length of the pattern.
Pros and Cons
Pros
The Rabin-Karp algorithm excels at multiple pattern matching, a feature that gives it an edge over other string searching algorithms. This is useful:
- Effective for detecting plagiarism, as it supports multiple pattern matching.
- Though theoretically not faster than brute force, its practical complexity is O(n+m).
- With a robust hashing function, it is efficient and straightforward to implement.
Cons
- There are several string matching algorithms with better performance than
O(n*m); however, Rabin-Karp outperforms the naive brute force method in the worst-case scenario. - It can be as slow as brute force in practice and requires additional memory.