Random Pick with Weight

Problem

You are given a 0-indexed array of positive integers w where w[i] describes the weight of the ith index.

You need to implement the function pickIndex(), which randomly picks an index in the range [0, w.length - 1] (inclusive) and returns it. The probability of picking an index i is w[i] / sum(w).

For example, if w = [1, 3], the probability of picking index 0 is 1 / (1 + 3) = 0.25 (i.e., 25%), and the probability of picking index 1 is 3 / (1 + 3) = 0.75 (i.e., 75%).

Examples

Example 1:

1
2
3
4
5
6
7
8
9


**Input**
["Solution","pickIndex"]
[[[1]],[]]
**Output**
[null,0]

**Explanation**
Solution solution = new Solution([1]);
solution.pickIndex(); // return 0. The only option is to return 0 since there is only one element in w.

Example 2:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


**Input**
["Solution","pickIndex","pickIndex","pickIndex","pickIndex","pickIndex"]
[[[1,3]],[]]
**Output**
[null,1,1,1,1,0]

**Explanation**
Solution solution = new Solution([1, 3]);
solution.pickIndex(); // return 1. It is returning the second element (index = 1) that has a probability of 3/4.
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 1
solution.pickIndex(); // return 0. It is returning the first element (index = 0) that has a probability of 1/4.

Since this is a randomization problem, multiple answers are allowed.
All of the following outputs can be considered correct:
[null,1,1,1,1,0]
[null,1,1,1,1,1]
[null,1,1,1,0,0]
[null,1,1,1,0,1]
[null,1,0,1,0,0]
......
and so on.

Solution

Method 1 – TreeMap for Weighted Segments

Intuition

We can think of weights on a straight line. Suppose w = [1,2,3], then:

So, when we call pick 6 times (6 is total of weights), then index 0 should show once, index 1 twice and index 2 3 times.

Suppose w = [1,2,3], then, the segments are:

Index 0: [0,1)
Index 1: [1,3)
Index 2: [3,6)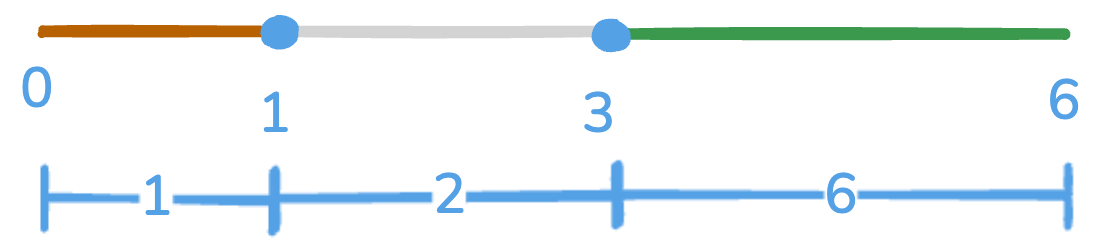

So we can think of the line parts as buckets or bars in straight line, where bar length is weight[i]. So, we can just total numbers, and whichever part the number falls on the bar or bucket is our answer.

To find the bucket, we need binary search, hence we are using Treemap.

By using a TreeMap, we can map the cumulative sum of weights to their corresponding indices. When picking an index, we generate a random number and use the TreeMap to quickly find the segment (index) it falls into, ensuring each index is picked with probability proportional to its weight.

A random number in [0,6) will fall into these segments according to their weights. More on Treemap: Java TreeMap Class.

Approach

Build a TreeMap mapping cumulative weights to indices.
When picking an index, generate a random number in [1, total].
Use TreeMap.ceilingKey to find the smallest key greater than or equal to the random number.
Return the corresponding index.

Complexity

⏰ Time complexity: O(log n) for pickIndex due to TreeMap lookup, O(n) for initialization.
🧺 Space complexity: O(n), for storing the TreeMap.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


// TreeMap equivalent in C++ is std::map
#include <vector>
#include <map>
#include <random>
using namespace std;
class Solution {
    map<int, int> tree;
    int total;
    mt19937 rng{random_device{}()};
    uniform_int_distribution<int> dist;
public:
    Solution(vector<int>& w) {
        int sum = 0;
        for (int i = 0; i < w.size(); ++i) {
            sum += w[i];
            tree[sum] = i;
        }
        total = sum;
        dist = uniform_int_distribution<int>(1, total);
    }
    int pickIndex() {
        int x = dist(rng);
        auto it = tree.lower_bound(x);
        return it->second;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


import java.util.*;
class Solution {
    private final TreeMap<Integer, Integer> tree = new TreeMap<>();
    private final int total;
    private final Random rand = new Random();
    public Solution(int[] w) {
        int sum = 0;
        for (int i = 0; i < w.length; i++) {
            sum += w[i];
            tree.put(sum, i);
        }
        total = sum;
    }
    public int pickIndex() {
        int x = rand.nextInt(total) + 1;
        return tree.ceilingEntry(x).getValue();
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


import random
class Solution:
    def __init__(self, w: list[int]) -> None:
        self.tree: dict[int, int] = {}
        self.total: int = 0
        for i, num in enumerate(w):
            self.total += num
            self.tree[self.total] = i
    def pickIndex(self) -> int:
        x = random.randint(1, self.total)
        keys = sorted(self.tree.keys())
        l, r = 0, len(keys) - 1
        while l < r:
            m = (l + r) // 2
            if keys[m] < x:
                l = m + 1
            else:
                r = m
        return self.tree[keys[l]]

Problem#

Examples#

Solution#

Method 1 – TreeMap for Weighted Segments#

Intuition#

Approach#

Complexity#

Code#