Range Minimum Query RMQ
Problem
Suppose we have an array:
+-------+-----+-----+-----+-----+-----+-----+
| Index | 0 | 1 | 2 | 3 | 4 | 5 |
+-------+-----+-----+-----+-----+-----+-----+
| Value | -1 | 3 | 4 | 0 | 2 | 1 |
+-------+-----+-----+-----+-----+-----+-----+
We want to perform some query on this array. For example:
- What is the minimum from index-2 to index-4? -> 0
- What is the maximum from index-0 to index-3? -> 4
- What is the summation from index-1 to index-5? -> 10
Examples
Example 1
Solution
Method 1 - Brute Force
We could traverse the array from the starting index to the finishing index and answer our query. In this approach, each query takes O(n) time where n is the difference between the starting index and finishing index. But what if there are millions of numbers and millions of queries? For m queries, it would take O(mn) time. So for 10⁵ values in our array, if we conduct 10⁵ queries, for worst case, we'll need to traverse 10¹⁰ items.
Method 2 - Dynamic Programming
We can create a 6X6 matrix to store the values for different ranges. For lookup[i][j] would store the min value from index i to index j.
Time complexity of building this matrix is O(n^2) and space complexity is also O(n^2). Then RMQ will take O(1).
For range minimum query(RMQ), our array would look like:
0 1 2 3 4 5
+-----+-----+-----+-----+-----+-----+-----+
| | -1 | 3 | 4 | 0 | 2 | 1 |
+-----+-----+-----+-----+-----+-----+-----+
0 | -1 | -1 | -1 | -1 | -1 | -1 | -1 |
+-----+-----+-----+-----+-----+-----+-----+
1 | 3 | | 3 | 3 | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+-----+-----+
2 | 4 | | | 4 | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+-----+-----+
3 | 0 | | | | 0 | 0 | 0 |
+-----+-----+-----+-----+-----+-----+-----+
4 | 2 | | | | | 2 | 1 |
+-----+-----+-----+-----+-----+-----+-----+
5 | 1 | | | | | | 1 |
+-----+-----+-----+-----+-----+-----+-----+
For example: The minimum from index-2 to index-4 is Matrix[2][4] = 0.
Code for preprocessing:
public void preprocess(int arr[]) {
int n = array.length;
int[][] lookup = new int[n][n];
// diagonal value have range 1, so they 1 element which is min
for (int i = 0; i<n; i++) {
lookup[i][i] = i;
}
// Fill rest of the entries in bottom up manner
for (int i = 0; i<n; i++) {
for (int j = i + 1; j<n; j++)
// To find minimum of [0,4],
// we compare minimum of
// arr[0][3] with arr[4].
if (lookup[i][j - 1]<arr[j]) {
lookup[i][j] = lookup[i][j - 1];
}
else {
lookup[i][j] = arr[j];
}
}
}
Now, when we get the query:
public int getMin(int l, int r) {
return preprocess[l][r]; // O(1)
}
Method 3 - Using Segment Tree 🏆
We can use segment tree data-structure.
It allows querying which of the stored segments contain a given point. It takes O(n) time to build a segment tree, it takes O(n) space to maintain it and it answers a query in O(logn) time.
Representation
Segment tree is a binary tree and the elements of the given array will be the leaves of that tree. We'll create the segment tree by dividing the array in half till we reach a single element.
- Leaf nodes: Contain elements of the input array.
- Internal nodes: Store the minimum value of all leaf nodes under them. The tree is represented using an array where:
- Left child of node
iis at2*i + 1. - Right child of node
iis at2*i + 2. - Parent node is at
(i - 1) // 2.
Construction
To build the segment tree from an array arr[0...n-1], recursively divide the range into two halves until each segment contains one element. Store the minimum value of each segment in a tree node.
The resulting tree is a Full Binary Tree with n leaves, n-1 internal nodes, and a total size of 2*n - 1. Its height is log2(n). The memory allocated for the segment tree is 2 * 2^log2(n) - 1.
So our division would provide us with:
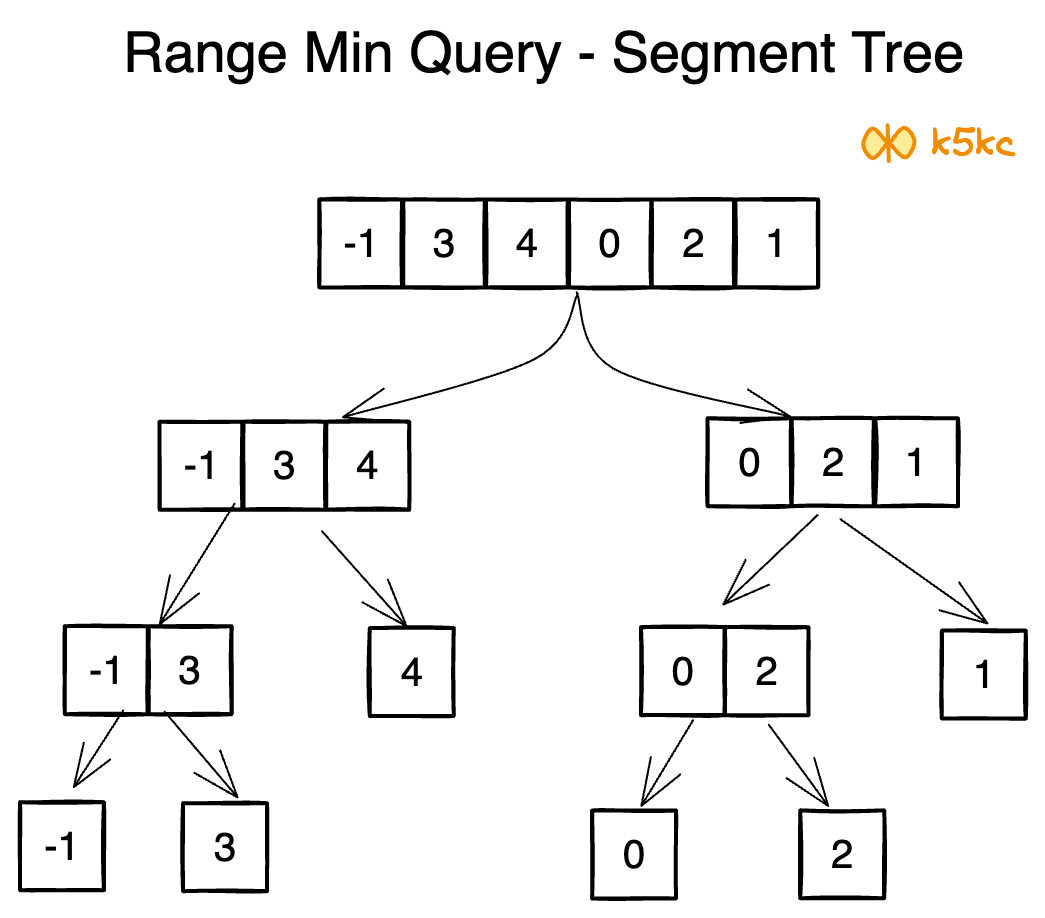
Now if we replace the non-leaf nodes with the minimum value of their leaves, we get:
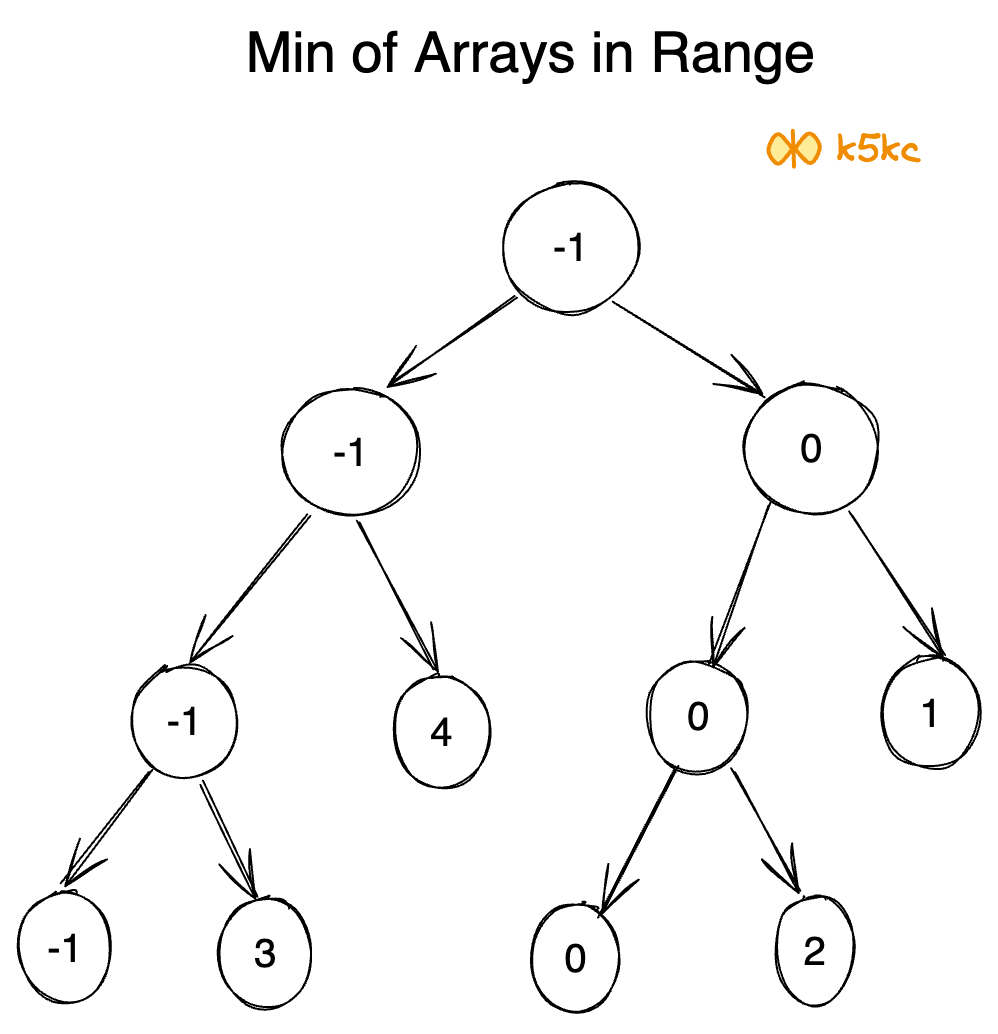
So this is our segment tree. We can notice that, the root node contains the minimum value of the whole array(range [0,5]), its left child contains the minimum value of our left array(range [0,2]), right child contains the minimum value of our right array(range [3,5]) and so on. The leaf nodes contain minimum value of each individual points. We get:
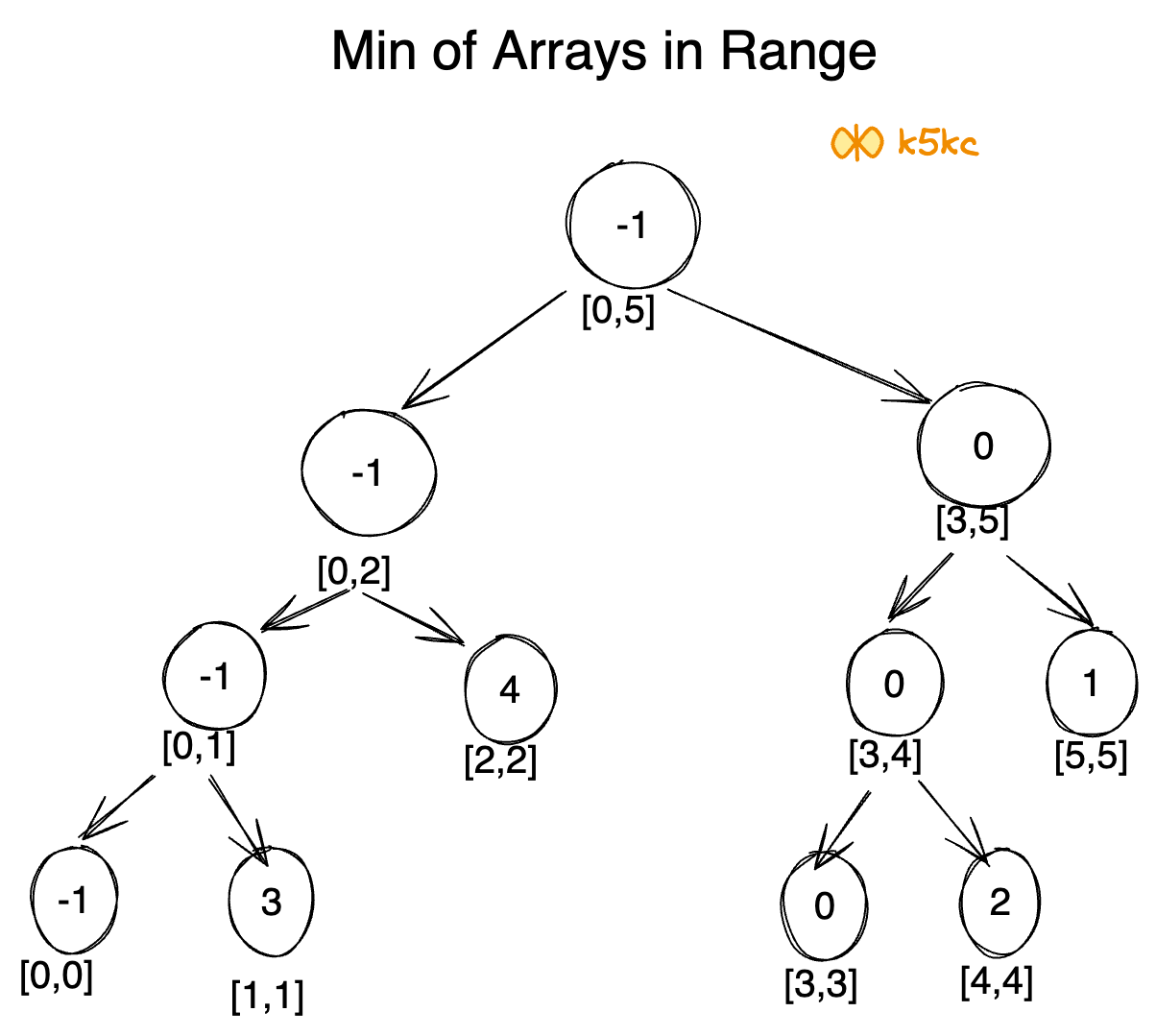
Querying
After constructing the segment tree, range minimum queries can be performed efficiently by utilising the precomputed minimums stored in its nodes.
To do a range query, we need to check three conditions:
- Partial Overlap: We check both leaves.
- Total Overlap: We return the value stored in the node.
- No Overlap: We return a very large value or infinity.
Let's say, we want to check range [2,4], that means we want to find the minimum from index-2 to 4. We'll start from the root and check if the range in our nodes is overlapped by our query range or not. Here,
[2,4]doesn't completely overlap[0,5]. So we'll check both directions.- At left subtree,
[2,4]partially overlaps[0,2]. We'll check both directions.- At left subtree,
[2,4]does not overlap[0,1], so this is not going to contribute to our answer. We return infinity. - At right subtree,
[2,4]totally overlaps[2,2]. We return 4. The minimum of these two returned values(4, infinity) is 4. We get 4 from this portion.
- At left subtree,
- At right subtree,
[2,4]partially overlaps. So we'll check both directions.- At left subtree,
[2,4]completely overlaps[3,4]. We return 0. - At right subtree,
[2,4]doesn't overlap[5,5]. We return infinity. The minimum of these two returned values(0, infinity) is 0. We get 0 from this portion.
- At left subtree,
- At left subtree,
- The minimum of the returned values(4,0) is 0. This is our desired minimum in range
[2,4].
Now we can check that, no matter what our query is, it would take maximum 4 steps to find the desired value from this segment tree.
Code
public class RangeMinQuery {
private final int n;
private final int[] segTree;
public RangeMinQuery(int n) {
this.n = n;
segTree = new int[2 * n];
}
void build(int[] a) {
// assign values to leaves of the segment tree
for (int i = 0; i < n; i++) {
segTree[n + i] = a[i];
}
/*
* assign values to internal nodes
* to compute minimum in a given range
*/
for (int i = n - 1; i >= 1; i--) {
segTree[i] = Math.min(segTree[2 * i], segTree[2 * i + 1]);
}
}
void update(int pos, int value) {
// change the index to leaf node first
pos += n;
// update the value at the leaf node
// at the exact index
segTree[pos] = value;
while (pos > 1) {
// move up one level at a time in the tree
pos >>= 1;
// update the values in the nodes in
// the next higher level
segTree[pos] = Math.min(segTree[2 * pos],
segTree[2 * pos + 1]);
}
}
int query(int left, int right) {
/*
* Basically the left and right indices will move
* towards right and left respectively and with
* every each next higher level and compute the
* minimum at each height. */
// change the index to leaf node first
left += n;
right += n;
// initialize minimum to a very high value
int mi = (int) 1e9;
while (left < right) {
// if left index is odd
if ((left & 1) == 1) {
mi = Math.min(mi, segTree[left]);
// make left index even
left++;
}
// if right index is odd
if ((right & 1) == 1) {
// make right index even
right--;
mi = Math.min(mi, segTree[right]);
}
// move to the next higher level
left /= 2;
right /= 2;
}
return mi;
}
// Driver Code
public static void main(String[] args) {
int[] a = {2, 6, 10, 4, 7, 28, 9, 11, 6, 33};
RangeMinQuery rmq = new RangeMinQuery(a.length);
/*
* Construct the segment tree by assigning
* the values to the internal nodes
*/
rmq.build(a);
// compute minimum in the range left to right
int left = 0, right = 5;
System.out.printf("Minimum in range %d to %d is %d\n",
left, right, rmq.query(
left, right + 1));
// update the value of index 3 to 1
int index = 3, value = 1;
// a[3] = 1;
// Contents of array : {2, 6, 10, 1, 7, 28, 9, 11, 6, 33}
rmq.update(index, value); // point update
// compute minimum in the range left to right
left = 2;
right = 6;
System.out.printf("Minimum in range %d to %d is %d\n",
left, right, rmq.query(
left, right + 1));
}
}
Method 4 - Square root composition
Square Root Decomposition provides an efficient way to reduce space usage compared to some other methods.
Preprocessing
- Divide the array
[0, n-1]into blocks of size approximately √n. - Compute and store the minimum value for each block.
This preprocessing step requires O(n) time and O(√n) space, as there are √n blocks and calculating the minimum for each block takes linear time.
Query
To calculate the minimum within a range [L, R], first retrieve the precomputed minimum values for the full blocks within the range. For partial overlaps at the start and end (corner blocks), scan these blocks linearly to determine their minimum.
Code
Java
class RangeMinQuery {
private int[] arr;
private int[] blocks;
private int blockSize;
public RangeMinQuery(int[] arr) {
this.arr = arr;
int n = arr.length;
this.blockSize = (int) Math.ceil(Math.sqrt(n));
this.blocks = new int[blockSize];
Arrays.fill(blocks, Integer.MAX_VALUE);
// Preprocess to compute minimum for each block
for (int i = 0; i < n; i++) {
int blockIndex = i / blockSize;
blocks[blockIndex] = Math.min(blocks[blockIndex], arr[i]);
}
}
public int query(int left, int right) {
int minValue = Integer.MAX_VALUE;
int startBlock = left / blockSize;
int endBlock = right / blockSize;
if (startBlock == endBlock) {
// Query falls within one block
for (int i = left; i <= right; i++) {
minValue = Math.min(minValue, arr[i]);
}
} else {
// Traverse the left partial block
for (int i = left; i < (startBlock + 1) * blockSize; i++) {
minValue = Math.min(minValue, arr[i]);
}
// Traverse full blocks between left and right
for (int i = startBlock + 1; i < endBlock; i++) {
minValue = Math.min(minValue, blocks[i]);
}
// Traverse the right partial block
for (int i = endBlock * blockSize; i <= right; i++) {
minValue = Math.min(minValue, arr[i]);
}
}
return minValue;
}
public static void main(String[] args) {
int[] arr = { 1, 3, 2, 7, 9, 11 };
int[][] queries = { { 1, 4 }, { 0, 2 } };
RangeMinQuery solution = new RangeMinQuery(arr);
for (int[] query : queries) {
System.out.println(solution.rangeQuery(query[0], query[1]));
}
// Output: 2, 1
}
}
Python
class RangeMinQuery:
def __init__(self, arr):
self.arr = arr
self.n = len(arr)
self.block_size = math.ceil(math.sqrt(self.n))
self.blocks = [float('inf')] * self.block_size
# Preprocess to compute minimum for each block
for i in range(self.n):
block_index = i // self.block_size
self.blocks[block_index] = min(self.blocks[block_index], arr[i])
def query(self, left, right):
min_value = float('inf')
start_block = left // self.block_size
end_block = right // self.block_size
if start_block == end_block:
# If the query falls within one block
for i in range(left, right + 1):
min_value = min(min_value, self.arr[i])
else:
# Traverse the left partial block
for i in range(left, (start_block + 1) * self.block_size):
min_value = min(min_value, self.arr[i])
# Traverse full blocks between left and right
for i in range(start_block + 1, end_block):
min_value = min(min_value, self.blocks[i])
# Traverse the right partial block
for i in range(end_block * self.block_size, right + 1):
min_value = min(min_value, self.arr[i])
return min_value
Complexity
- ⏰ Time complexity:
O(√n). The query operation has a time complexity of O(√n), as middle blocks can be accessed directly, and we process at most 2 * O(√n) elements from the corner blocks. Thus, overall complexity remains efficient at O(√n). - 🧺 Space complexity:
O(n)
Method 4 - Sparse table
Sparse tables are precomputed data structures that allow range queries answers in O(1) time by using values precomputed during preprocessing. Sparse tables work for immutable arrays.
Code
Java
class RangeMinQuery {
private int[][] sparseTable;
private int[] log;
private int n;
public Solution(int[] arr) {
this.n = arr.length;
this.log = new int[n + 1];
for (int i = 2; i <= n; i++) {
log[i] = log[i / 2] + 1;
}
int maxLog = log[n];
this.sparseTable = new int[n][maxLog + 1];
buildSparseTable(arr);
}
private void buildSparseTable(int[] arr) {
for (int i = 0; i < n; i++) {
sparseTable[i][0] = arr[i];
}
for (int j = 1; j <= log[n]; j++) {
for (int i = 0; i + (1 << j) <= n; i++) {
sparseTable[i][j] = Math.min(
sparseTable[i][j - 1],
sparseTable[i + (1 << (j - 1))][j - 1]
);
}
}
}
public int query(int left, int right) {
int length = right - left + 1;
int j = log[length];
return Math.min(
sparseTable[left][j],
sparseTable[right - (1 << j) + 1][j]
);
}
public static void main(String[] args) {
int[] arr = { 1, 3, 2, 7, 9, 11 };
int[][] queries = { { 1, 4 }, { 0, 2 } };
Solution solution = new Solution(arr);
for (int[] query : queries) {
System.out.println(solution.rangeQuery(query[0], query[1]));
}
// Output: 2, 1
}
}
Python
class RangeMinQuery:
def __init__(self, arr):
self.arr = arr
self.n = len(arr)
self.log = [0] * (self.n + 1)
for i in range(2, self.n + 1):
self.log[i] = self.log[i // 2] + 1
self.sparse_table = [[0] * (self.log[self.n] + 1) for _ in range(self.n)]
self.build_sparse_table()
def build_sparse_table(self):
for i in range(self.n):
self.sparse_table[i][0] = self.arr[i]
for j in range(1, self.log[self.n] + 1):
for i in range(self.n - (1 << j) + 1):
self.sparse_table[i][j] = min(
self.sparse_table[i][j - 1],
self.sparse_table[i + (1 << (j - 1))][j - 1]
)
def query(self, left, right):
length = right - left + 1
j = self.log[length]
return min(
self.sparse_table[left][j],
self.sparse_table[right - (1 << j) + 1][j]
)
Complexity
- ⏰ Time complexity:
O(1)for query, butO(n log n)for preprocessing. - 🧺 Space complexity:
O(n)