problemeasyalgorithmsleetcode-938leetcode 938leetcode938daily-coding-problem-343daily coding problem 343dailycodingproblem343

Range Sum of BST

EasyUpdated: Aug 10, 2025
Practice on:
LeetCode

Problem

Given the root node of a binary search tree and two integers low and high, return _the sum of values of all nodes with a value in theinclusive range _[low, high].

Examples

Example 1

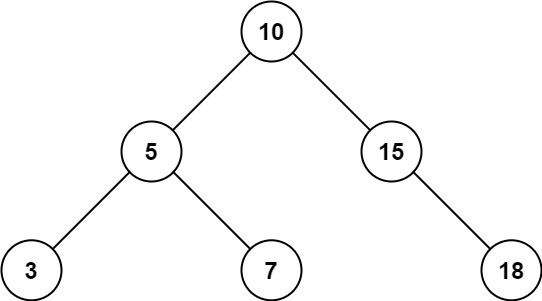
Input: root = [10,5,15,3,7,null,18], low = 7, high = 15
Output: 32
Explanation: Nodes 7, 10, and 15 are in the range [7, 15]. 7 + 10 + 15 = 32.

Example 2

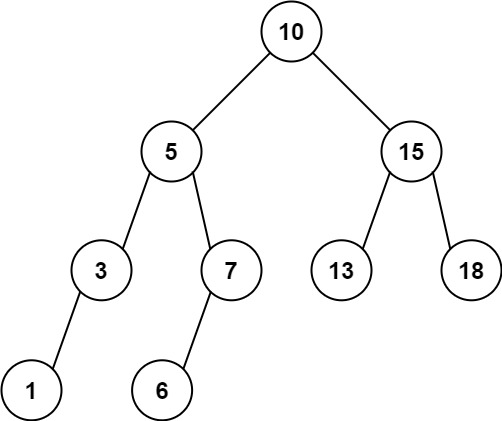
Input: root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
Output: 23
Explanation: Nodes 6, 7, and 10 are in the range [6, 10]. 6 + 7 + 10 = 23.

Constraints

  • The number of nodes in the tree is in the range [1, 2 * 10^4].
  • 1 <= Node.val <= 10^5
  • 1 <= low <= high <= 10^5
  • All Node.val are unique.

Solution

Method 1 – DFS with BST Pruning

Intuition

Since the tree is a BST, we can skip entire subtrees that are out of the [low, high] range, making the traversal more efficient than a naive DFS.

Approach

  1. Traverse the tree recursively (DFS).
  2. If the current node's value is less than low, only search the right subtree.
  3. If the current node's value is greater than high, only search the left subtree.
  4. If the current node's value is within [low, high], add it to the sum and search both subtrees.

Code

C++
class Solution {
public:
    int rangeSumBST(TreeNode* root, int low, int high) {
        if (!root) return 0;
        if (root->val < low) return rangeSumBST(root->right, low, high);
        if (root->val > high) return rangeSumBST(root->left, low, high);
        return root->val + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);
    }
};
Go
func rangeSumBST(root *TreeNode, low int, high int) int {
    if root == nil {
        return 0
    }
    if root.Val < low {
        return rangeSumBST(root.Right, low, high)
    }
    if root.Val > high {
        return rangeSumBST(root.Left, low, high)
    }
    return root.Val + rangeSumBST(root.Left, low, high) + rangeSumBST(root.Right, low, high)
}
Java
class Solution {
    public int rangeSumBST(TreeNode root, int low, int high) {
        if (root == null) return 0;
        if (root.val < low) return rangeSumBST(root.right, low, high);
        if (root.val > high) return rangeSumBST(root.left, low, high);
        return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
    }
}
Kotlin
class Solution {
    fun rangeSumBST(root: TreeNode?, low: Int, high: Int): Int {
        if (root == null) return 0
        if (root.`val` < low) return rangeSumBST(root.right, low, high)
        if (root.`val` > high) return rangeSumBST(root.left, low, high)
        return root.`val` + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high)
    }
}
Python
from typing import Optional
class Solution:
    def rangeSumBST(self, root: Optional['TreeNode'], low: int, high: int) -> int:
        if not root:
            return 0
        if root.val < low:
            return self.rangeSumBST(root.right, low, high)
        if root.val > high:
            return self.rangeSumBST(root.left, low, high)
        return root.val + self.rangeSumBST(root.left, low, high) + self.rangeSumBST(root.right, low, high)
Rust
impl Solution {
    pub fn range_sum_bst(root: Option<Rc<RefCell<TreeNode>>>, low: i32, high: i32) -> i32 {
        match root {
            Some(node) => {
                let n = node.borrow();
                if n.val < low {
                    Solution::range_sum_bst(n.right.clone(), low, high)
                } else if n.val > high {
                    Solution::range_sum_bst(n.left.clone(), low, high)
                } else {
                    n.val + Solution::range_sum_bst(n.left.clone(), low, high) + Solution::range_sum_bst(n.right.clone(), low, high)
                }
            },
            None => 0
        }
    }
}
TypeScript
function rangeSumBST(root: TreeNode | null, low: number, high: number): number {
    if (!root) return 0;
    if (root.val < low) return rangeSumBST(root.right, low, high);
    if (root.val > high) return rangeSumBST(root.left, low, high);
    return root.val + rangeSumBST(root.left, low, high) + rangeSumBST(root.right, low, high);
}

Complexity

  • ⏰ Time complexity: O(n), where n is the number of nodes. In the worst case, all nodes are visited, but pruning often reduces the number of recursive calls.
  • 🧺 Space complexity: O(h), where h is the height of the tree, due to the recursion stack.

Comments