Range Sum Query 2D - Immutable

Problem

Given a 2D matrix matrix, handle multiple queries of the following type:

• Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

• NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
• int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Examples

Example 1:

**Input**
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
**Output**
[null, 8, 11, 12]

**Explanation**
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
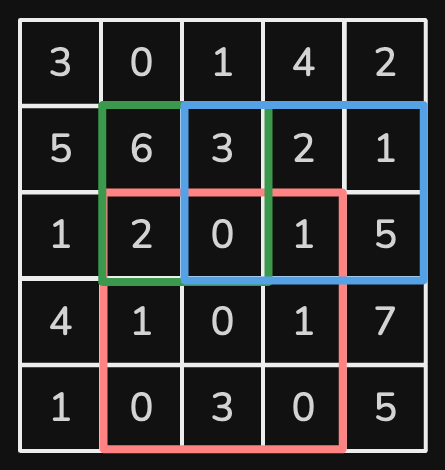
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Solution

Method 1 - Prefix Sum

To optimise multiple calls to the sumRegion method, we preprocess the matrix to create a prefix sum matrix. An array prefix[][] is defined to hold the cumulative sum from (0, 0) to each cell in the matrix.

Prefix Sum Matrix Construction

For a given cell (i, j) in the prefix sum matrix, i.e. prefix[i][j], it stores the sum of elements in the rectangle from the top-left (0, 0) to (i, j) of the original matrix.

Now, if someone queries for sum of green region below:

As value at [0][0] appears twice, we we have to add it back.

So, the formula to calculate prefix sum is:

prefix[i][j] = matrix[i][j] + prefix[i-1][j] + prefix[i][j-1] - prefix[i-1][j-1]

This is how the formula using prefix sum looks:

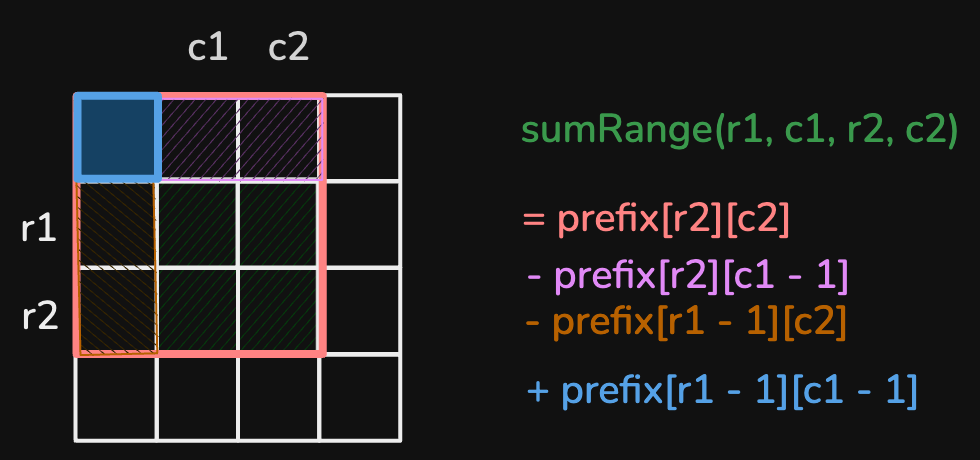
Code

Java

class Solution {
    private int[][] prefix;

    public Solution(int[][] matrix) {
        int rows = matrix.length, cols = matrix[0].length;
        prefix = new int[rows][cols];

        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                prefix[i][j] = matrix[i][j];
                if (i > 0) prefix[i][j] += prefix[i - 1][j];
                if (j > 0) prefix[i][j] += prefix[i][j - 1];
                if (i > 0 && j > 0) prefix[i][j] -= prefix[i - 1][j - 1];
            }
        }
    }

    public int sumRegion(int row1, int col1, int row2, int col2) {
        int ans = prefix[row2][col2];
        if (row1 > 0) ans -= prefix[row1 - 1][col2];
        if (col1 > 0) ans -= prefix[row2][col1 - 1];
        if (row1 > 0 && col1 > 0) ans += prefix[row1 - 1][col1 - 1];
        return ans;
    }
}

Python

class Solution:
    def __init__(self, matrix: List[List[int]]) -> None:
        rows, cols = len(matrix), len(matrix[0])
        self.prefix = [[0] * cols for _ in range(rows)]

        for i in range(rows):
            for j in range(cols):
                self.prefix[i][j] = matrix[i][j]
                if i > 0:
                    self.prefix[i][j] += self.prefix[i - 1][j]
                if j > 0:
                    self.prefix[i][j] += self.prefix[i][j - 1]
                if i > 0 and j > 0:
                    self.prefix[i][j] -= self.prefix[i - 1][j - 1]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        ans = self.prefix[row2][col2]
        if row1 > 0:
            ans -= self.prefix[row1 - 1][col2]
        if col1 > 0:
            ans -= self.prefix[row2][col1 - 1]
        if row1 > 0 and col1 > 0:
            ans += self.prefix[row1 - 1][col1 - 1]
        return ans

Complexity

• ⏰ Time complexity
  • Preprocessing in constructor: O(m * n), where m is the number of rows and n is the number of columns.
  • Query: O(1) for each sumRegion query.
• 🧺 Space complexity: O(m * n) for the prefix sum matrix.