Rank Transform of a Matrix
HardUpdated: Aug 2, 2025
Practice on:
Problem
Given an m x n matrix, return a new matrixanswer
whereanswer[row][col]is the _rank of _matrix[row][col].
The rank is an integer that represents how large an element is compared to other elements. It is calculated using the following rules:
- The rank is an integer starting from
1. - If two elements
pandqare in the same row or column , then: - If
p < qthenrank(p) < rank(q) - If
p == qthenrank(p) == rank(q) - If
p > qthenrank(p) > rank(q)- The rank should be as small as possible.
The test cases are generated so that answer is unique under the given rules.
Examples
Example 1
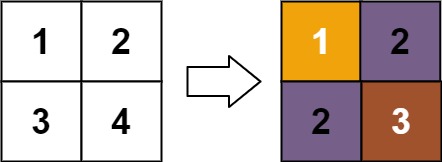
Input: matrix = [[1,2],[3,4]]
Output: [[1,2],[2,3]]
Explanation:
The rank of matrix[0][0] is 1 because it is the smallest integer in its row and column.
The rank of matrix[0][1] is 2 because matrix[0][1] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][0] is 2 because matrix[1][0] > matrix[0][0] and matrix[0][0] is rank 1.
The rank of matrix[1][1] is 3 because matrix[1][1] > matrix[0][1], matrix[1][1] > matrix[1][0], and both matrix[0][1] and matrix[1][0] are rank 2.
Example 2
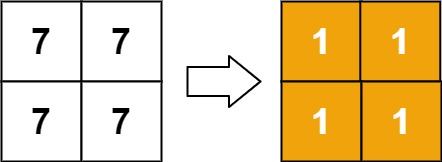
Input: matrix = [[7,7],[7,7]]
Output: [[1,1],[1,1]]
Example 3
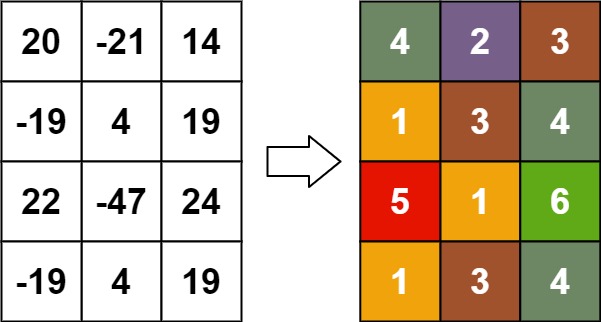
Input: matrix = [[20,-21,14],[-19,4,19],[22,-47,24],[-19,4,19]]
Output: [[4,2,3],[1,3,4],[5,1,6],[1,3,4]]
Constraints
m == matrix.lengthn == matrix[i].length1 <= m, n <= 500-10^9 <= matrix[row][col] <= 10^9
Solution
Method 1 – Union-Find with Value Grouping
Intuition
The key idea is to process matrix values in increasing order, grouping equal values in the same row or column using union-find. This ensures that all constraints are satisfied and ranks are assigned minimally.
Approach
- For each unique value in the matrix, collect all its positions.
- For each value, use union-find to group positions in the same row or column.
- For each group, determine the maximum rank among all rows and columns involved, then assign rank + 1 to all positions in the group.
- Update the row and column ranks accordingly.
- Repeat for all values in increasing order.
Code
C++
class Solution {
public:
vector<vector<int>> matrixRankTransform(vector<vector<int>>& mat) {
int m = mat.size(), n = mat[0].size();
map<int, vector<pair<int, int>>> val2pos;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
val2pos[mat[i][j]].emplace_back(i, j);
vector<int> row(m), col(n);
vector<vector<int>> ans(m, vector<int>(n));
for (auto& [val, pos] : val2pos) {
vector<int> p(m + n);
iota(p.begin(), p.end(), 0);
function<int(int)> find = [&](int x) { return p[x] == x ? x : p[x] = find(p[x]); };
for (auto& [i, j] : pos) p[find(i)] = find(j + m);
unordered_map<int, int> groupMax;
for (auto& [i, j] : pos) {
int g = find(i);
groupMax[g] = max(groupMax[g], max(row[i], col[j]));
}
for (auto& [i, j] : pos) {
int g = find(i);
ans[i][j] = groupMax[g] + 1;
}
for (auto& [i, j] : pos) {
row[i] = ans[i][j];
col[j] = ans[i][j];
}
}
return ans;
}
};
Go
func matrixRankTransform(mat [][]int) [][]int {
m, n := len(mat), len(mat[0])
type pair struct{ i, j int }
val2pos := map[int][]pair{}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
val2pos[mat[i][j]] = append(val2pos[mat[i][j]], pair{i, j})
}
}
row := make([]int, m)
col := make([]int, n)
ans := make([][]int, m)
for i := range ans {
ans[i] = make([]int, n)
}
keys := make([]int, 0, len(val2pos))
for k := range val2pos {
keys = append(keys, k)
}
sort.Ints(keys)
for _, val := range keys {
pos := val2pos[val]
p := make([]int, m+n)
for i := range p {
p[i] = i
}
var find func(int) int
find = func(x int) int {
if p[x] != x {
p[x] = find(p[x])
}
return p[x]
}
for _, v := range pos {
p[find(v.i)] = find(v.j + m)
}
groupMax := map[int]int{}
for _, v := range pos {
g := find(v.i)
if groupMax[g] < row[v.i] {
groupMax[g] = row[v.i]
}
if groupMax[g] < col[v.j] {
groupMax[g] = col[v.j]
}
}
for _, v := range pos {
g := find(v.i)
ans[v.i][v.j] = groupMax[g] + 1
}
for _, v := range pos {
row[v.i] = ans[v.i][v.j]
col[v.j] = ans[v.i][v.j]
}
}
return ans
}
Java
class Solution {
public int[][] matrixRankTransform(int[][] mat) {
int m = mat.length, n = mat[0].length;
Map<Integer, List<int[]>> val2pos = new TreeMap<>();
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
val2pos.computeIfAbsent(mat[i][j], k -> new ArrayList<>()).add(new int[]{i, j});
int[] row = new int[m], col = new int[n];
int[][] ans = new int[m][n];
for (int val : val2pos.keySet()) {
List<int[]> pos = val2pos.get(val);
int[] p = new int[m + n];
for (int i = 0; i < m + n; ++i) p[i] = i;
Function<Integer, Integer> find = new Function<>() {
public Integer apply(Integer x) {
if (p[x] != x) p[x] = this.apply(p[x]);
return p[x];
}
};
for (int[] v : pos) p[find.apply(v[0])] = find.apply(v[1] + m);
Map<Integer, Integer> groupMax = new HashMap<>();
for (int[] v : pos) {
int g = find.apply(v[0]);
groupMax.put(g, Math.max(groupMax.getOrDefault(g, 0), Math.max(row[v[0]], col[v[1]])));
}
for (int[] v : pos) {
int g = find.apply(v[0]);
ans[v[0]][v[1]] = groupMax.get(g) + 1;
}
for (int[] v : pos) {
row[v[0]] = ans[v[0]][v[1]];
col[v[1]] = ans[v[0]][v[1]];
}
}
return ans;
}
}
Kotlin
class Solution {
fun matrixRankTransform(mat: Array<IntArray>): Array<IntArray> {
val m = mat.size
val n = mat[0].size
val val2pos = sortedMapOf<Int, MutableList<Pair<Int, Int>>>()
for (i in 0 until m)
for (j in 0 until n)
val2pos.getOrPut(mat[i][j]) { mutableListOf() }.add(i to j)
val row = IntArray(m)
val col = IntArray(n)
val ans = Array(m) { IntArray(n) }
for ((_, pos) in val2pos) {
val p = IntArray(m + n) { it }
fun find(x: Int): Int = if (p[x] == x) x else { p[x] = find(p[x]); p[x] }
for ((i, j) in pos) p[find(i)] = find(j + m)
val groupMax = mutableMapOf<Int, Int>()
for ((i, j) in pos) {
val g = find(i)
groupMax[g] = maxOf(groupMax.getOrDefault(g, 0), row[i], col[j])
}
for ((i, j) in pos) {
val g = find(i)
ans[i][j] = groupMax[g]!! + 1
}
for ((i, j) in pos) {
row[i] = ans[i][j]
col[j] = ans[i][j]
}
}
return ans
}
}
Python
from typing import List
class Solution:
def matrixRankTransform(self, mat: List[List[int]]) -> List[List[int]]:
m, n = len(mat), len(mat[0])
from collections import defaultdict
val2pos = defaultdict(list)
for i in range(m):
for j in range(n):
val2pos[mat[i][j]].append((i, j))
row = [0] * m
col = [0] * n
ans = [[0] * n for _ in range(m)]
for val in sorted(val2pos):
p = list(range(m + n))
def find(x):
if p[x] != x:
p[x] = find(p[x])
return p[x]
for i, j in val2pos[val]:
p[find(i)] = find(j + m)
groupMax = dict()
for i, j in val2pos[val]:
g = find(i)
groupMax[g] = max(groupMax.get(g, 0), row[i], col[j])
for i, j in val2pos[val]:
g = find(i)
ans[i][j] = groupMax[g] + 1
for i, j in val2pos[val]:
row[i] = ans[i][j]
col[j] = ans[i][j]
return ans
Rust
impl Solution {
pub fn matrix_rank_transform(mat: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
use std::collections::{BTreeMap, HashMap};
let m = mat.len();
let n = mat[0].len();
let mut val2pos = BTreeMap::new();
for i in 0..m {
for j in 0..n {
val2pos.entry(mat[i][j]).or_insert(vec![]).push((i, j));
}
}
let mut row = vec![0; m];
let mut col = vec![0; n];
let mut ans = vec![vec![0; n]; m];
for (_val, pos) in val2pos {
let mut p: Vec<usize> = (0..m + n).collect();
fn find(p: &mut Vec<usize>, x: usize) -> usize {
if p[x] != x {
p[x] = find(p, p[x]);
}
p[x]
}
for &(i, j) in &pos {
let pi = find(&mut p, i);
let pj = find(&mut p, j + m);
p[pi] = pj;
}
let mut group_max = HashMap::new();
for &(i, j) in &pos {
let g = find(&mut p, i);
let v = *group_max.get(&g).unwrap_or(&0);
group_max.insert(g, v.max(row[i]).max(col[j]));
}
for &(i, j) in &pos {
let g = find(&mut p, i);
ans[i][j] = group_max[&g] + 1;
}
for &(i, j) in &pos {
row[i] = ans[i][j];
col[j] = ans[i][j];
}
}
ans
}
}
TypeScript
class Solution {
matrixRankTransform(mat: number[][]): number[][] {
const m = mat.length, n = mat[0].length;
const val2pos = new Map<number, [number, number][]>()
for (let i = 0; i < m; ++i)
for (let j = 0; j < n; ++j) {
if (!val2pos.has(mat[i][j])) val2pos.set(mat[i][j], [])
val2pos.get(mat[i][j])!.push([i, j])
}
const row = Array(m).fill(0), col = Array(n).fill(0)
const ans = Array.from({ length: m }, () => Array(n).fill(0))
const keys = Array.from(val2pos.keys()).sort((a, b) => a - b)
for (const val of keys) {
const pos = val2pos.get(val)!
const p = Array(m + n).fill(0).map((_, i) => i)
const find = (x: number): number => p[x] === x ? x : (p[x] = find(p[x]))
for (const [i, j] of pos) p[find(i)] = find(j + m)
const groupMax = new Map<number, number>()
for (const [i, j] of pos) {
const g = find(i)
groupMax.set(g, Math.max(groupMax.get(g) ?? 0, row[i], col[j]))
}
for (const [i, j] of pos) {
const g = find(i)
ans[i][j] = groupMax.get(g)! + 1
}
for (const [i, j] of pos) {
row[i] = ans[i][j]
col[j] = ans[i][j]
}
}
return ans
}
}
Complexity
- ⏰ Time complexity:
O((m * n) * α(m + n)), where α is the inverse Ackermann function, due to union-find operations for each unique value and all positions. Sorting values and iterating over all cells is alsoO(m * n log(m * n))in the worst case. - 🧺 Space complexity:
O(m * n), for storing mappings, union-find parent arrays, and the answer matrix.