Problem

Given two rectangles on a plane. We are given bottom left and top right points of the two rectangles. We need to find the total area.

OR

Given the coordinates of two rectilinear rectangles in a 2D plane, return the total area covered by the two rectangles.

The first rectangle is defined by its bottom-left corner (ax1, ay1) and its top-right corner (ax2, ay2).

The second rectangle is defined by its bottom-left corner (bx1, by1) and its top-right corner (bx2, by2).

Examples

Example 1

1
2

Input: ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
Output: 45

Example 2

1
2

Input: ax1 = -2, ay1 = -2, ax2 = 2, ay2 = 2, bx1 = -2, by1 = -2, bx2 = 2, by2 = 2
Output: 16

Solution

Method 1 – Area by Inclusion-Exclusion (with Overlap Visualization)

Intuition

Suppose we have two rectangles:

1
2

Rectangle 1: bottom-left (a, b), top-right (c, d)
Rectangle 2: bottom-left (e, f), top-right (g, h)

Now, we can calculate the area of rectangle as:

1
2
3

x_distance for 1st rectangle = abs(c – a)
y_distance for 1st rectangle = abs(d - b)
area1 = (c - a) * (d - b)

Similarly, we can compute area of second rectangle:

1

area2 = (g - e) * (h - f)

To find the total area covered by these two rectangles, we need to account for any overlap between them. If the rectangles do not overlap, the total area is simply the sum of their individual areas. If they do overlap, the overlapping region is counted twice, so we must subtract the area of the intersection once.

The excalidraw image below visually demonstrates the two rectangles and their possible overlap:

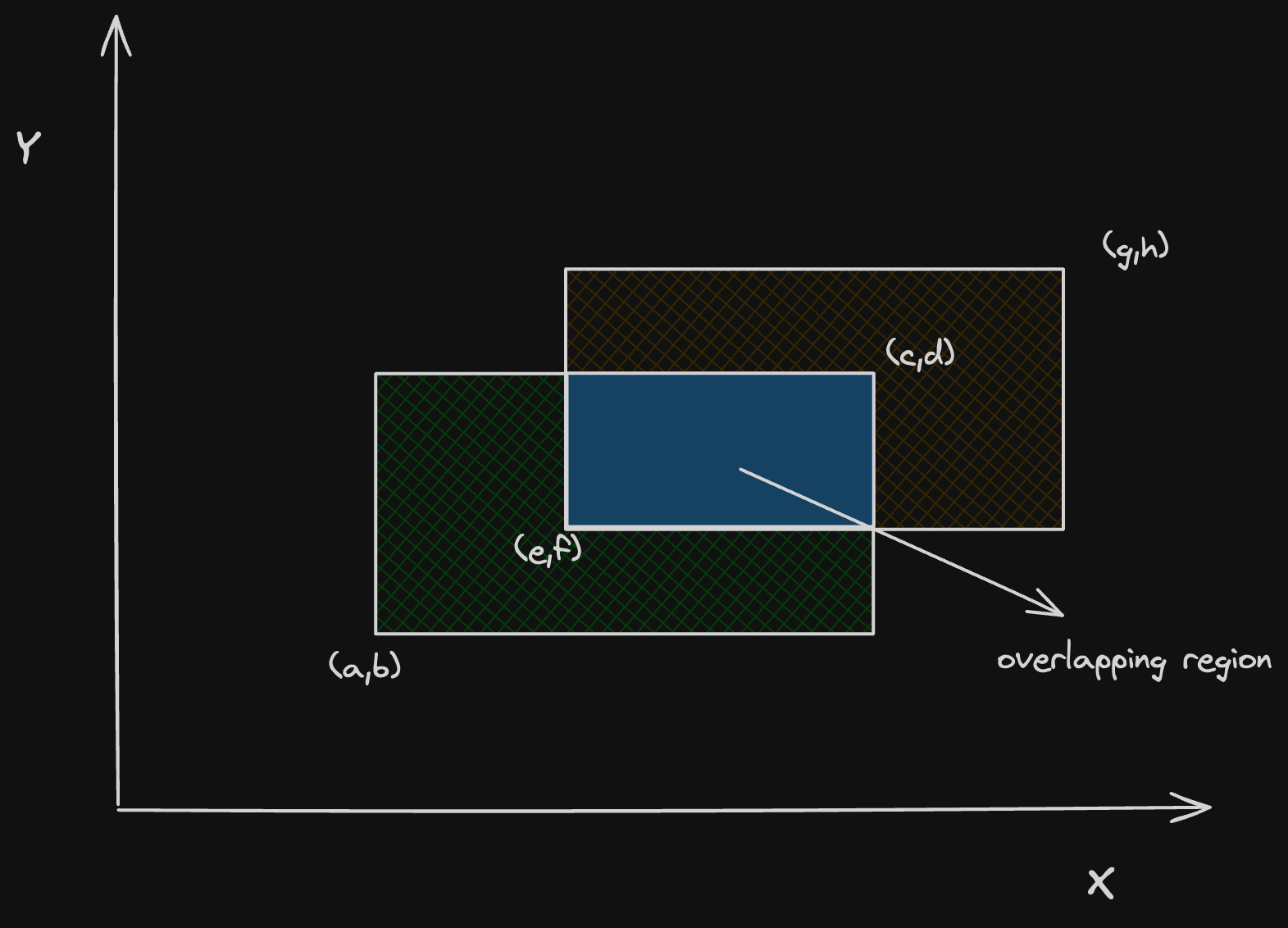
Approach

  1. Calculate the area of each rectangle separately:
    • For rectangle 1 (bottom-left (a, b), top-right (c, d)):
    • Area = (c - a) * (d - b)
    • For rectangle 2 (bottom-left (e, f), top-right (g, h)):
    • Area = (g - e) * (h - f)
  2. Find the overlap (intersection) region, if any:
    • The overlap along the x-axis is from max(a, e) to min(c, g)
    • The overlap along the y-axis is from max(b, f) to min(d, h)
    • If these intervals are valid (i.e., right > left and top > bottom), the intersection area is:
    • Overlap Area = (min(c, g) - max(a, e)) * (min(d, h) - max(b, f))
    • If there is no overlap, the overlap area is 0.
  3. Apply the inclusion-exclusion principle:
    • Total Area = (Area of Rectangle 1) + (Area of Rectangle 2) - (Overlap Area)

This approach ensures that the overlapping region is not double-counted, and the excalidraw diagram helps visualize how the rectangles and their intersection are determined.

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int area1 = (ax2 - ax1) * (ay2 - ay1);
        int area2 = (bx2 - bx1) * (by2 - by1);
        int overlapX = std::max(0, std::min(ax2, bx2) - std::max(ax1, bx1));
        int overlapY = std::max(0, std::min(ay2, by2) - std::max(ay1, by1));
        int overlap = overlapX * overlapY;
        return area1 + area2 - overlap;
    }
};
Go
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

func computeArea(ax1, ay1, ax2, ay2, bx1, by1, bx2, by2 int) int {
    area1 := (ax2 - ax1) * (ay2 - ay1)
    area2 := (bx2 - bx1) * (by2 - by1)
    overlapX := max(0, min(ax2, bx2) - max(ax1, bx1))
    overlapY := max(0, min(ay2, by2) - max(ay1, by1))
    overlap := overlapX * overlapY
    return area1 + area2 - overlap
}
func min(a, b int) int { if a < b { return a }; return b }
func max(a, b int) int { if a > b { return a }; return b }
Java
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution {
    public int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int area1 = (ax2 - ax1) * (ay2 - ay1);
        int area2 = (bx2 - bx1) * (by2 - by1);
        int overlapX = Math.max(0, Math.min(ax2, bx2) - Math.max(ax1, bx1));
        int overlapY = Math.max(0, Math.min(ay2, by2) - Math.max(ay1, by1));
        int overlap = overlapX * overlapY;
        return area1 + area2 - overlap;
    }
}
Kotlin
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution {
    fun computeArea(ax1: Int, ay1: Int, ax2: Int, ay2: Int, bx1: Int, by1: Int, bx2: Int, by2: Int): Int {
        val area1 = (ax2 - ax1) * (ay2 - ay1)
        val area2 = (bx2 - bx1) * (by2 - by1)
        val overlapX = maxOf(0, minOf(ax2, bx2) - maxOf(ax1, bx1))
        val overlapY = maxOf(0, minOf(ay2, by2) - maxOf(ay1, by1))
        val overlap = overlapX * overlapY
        return area1 + area2 - overlap
    }
}
Python
1
2
3
4
5
6
7
8

class Solution:
    def computeArea(self, ax1, ay1, ax2, ay2, bx1, by1, bx2, by2):
        area1 = (ax2 - ax1) * (ay2 - ay1)
        area2 = (bx2 - bx1) * (by2 - by1)
        overlapX = max(0, min(ax2, bx2) - max(ax1, bx1))
        overlapY = max(0, min(ay2, by2) - max(ay1, by1))
        overlap = overlapX * overlapY
        return area1 + area2 - overlap
Rust
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

impl Solution {
    pub fn compute_area(ax1: i32, ay1: i32, ax2: i32, ay2: i32, bx1: i32, by1: i32, bx2: i32, by2: i32) -> i32 {
        let area1 = (ax2 - ax1) * (ay2 - ay1);
        let area2 = (bx2 - bx1) * (by2 - by1);
        let overlap_x = (ax2.min(bx2) - ax1.max(bx1)).max(0);
        let overlap_y = (ay2.min(by2) - ay1.max(by1)).max(0);
        let overlap = overlap_x * overlap_y;
        area1 + area2 - overlap
    }
}
TypeScript
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

class Solution {
    computeArea(ax1: number, ay1: number, ax2: number, ay2: number, bx1: number, by1: number, bx2: number, by2: number): number {
        const area1 = (ax2 - ax1) * (ay2 - ay1);
        const area2 = (bx2 - bx1) * (by2 - by1);
        const overlapX = Math.max(0, Math.min(ax2, bx2) - Math.max(ax1, bx1));
        const overlapY = Math.max(0, Math.min(ay2, by2) - Math.max(ay1, by1));
        const overlap = overlapX * overlapY;
        return area1 + area2 - overlap;
    }
}

Complexity

  • ⏰ Time complexity: O(1). All calculations (area and overlap) are done with a constant number of arithmetic and comparison operations.
  • 🧺 Space complexity: O(1). Only a constant amount of extra space is used for variables.