Remove All Ones With Row and Column Flips

Problem

You are given an m x n binary matrix grid.

In one operation, you can choose any row or column and flip each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Return true if it is possible to remove all1 _' s from _grid using any number of operations or false otherwise.

Examples

Example 1:

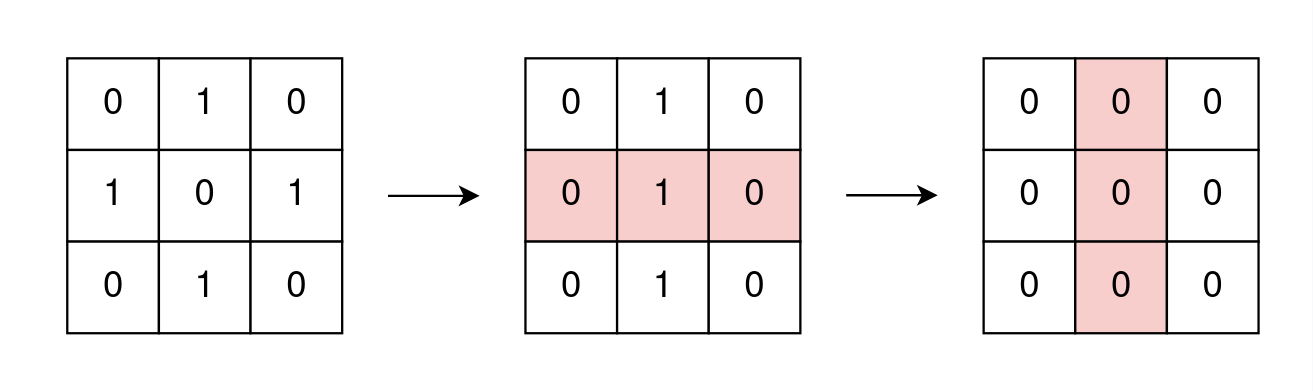
Input: grid = [[0,1,0],[1,0,1],[0,1,0]]
Output: true
Explanation: One possible way to remove all 1's from grid is to:
- Flip the middle row
- Flip the middle column

Example 2:

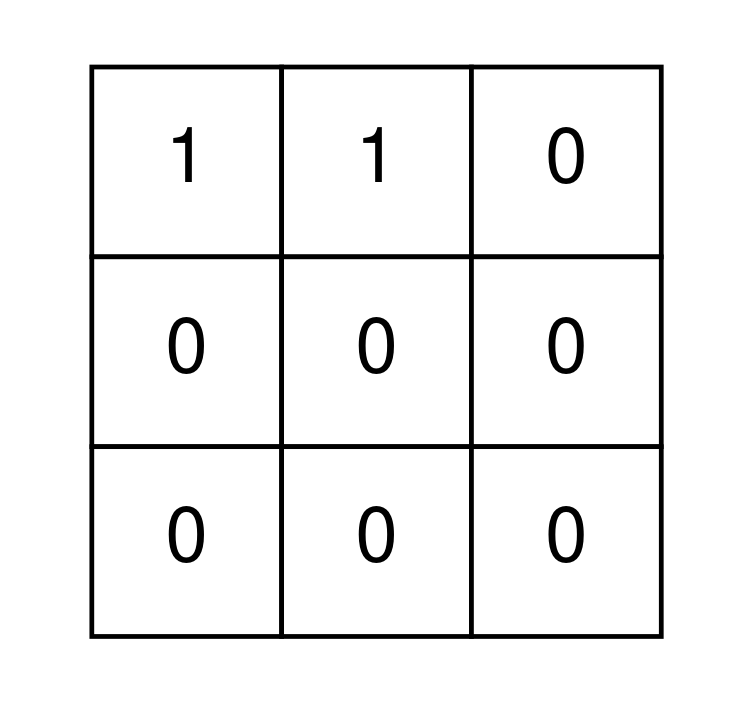
Input: grid = [[1,1,0],[0,0,0],[0,0,0]]
Output: false
Explanation: It is impossible to remove all 1's from grid.

Example 3:

Input: grid = [[0]]
Output: true
Explanation: There are no 1's in grid.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] is either 0 or 1.

Solution

Method 1 – Row Pattern Consistency (Bit Manipulation)

Intuition

If we can flip any row or column, the only thing that matters is the pattern of 0s and 1s in each row. If two rows are different, we can flip columns to make them the same, but only if their difference is consistent (i.e., every bit is flipped or not). So, for all rows, either they are the same as the first row, or the bitwise inverse of the first row.

Approach

1. Take the first row as a reference.
2. For each row, check if it is either identical to the first row or its bitwise inverse.
3. If all rows satisfy this, it is possible to remove all ones; otherwise, it is not.
4. This works because flipping a row or column is equivalent to toggling bits, and the only way to reach all zeros is if all rows can be made the same by column flips.

Code

C++

class Solution {
public:
    bool removeOnes(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        for (int i = 1; i < m; ++i) {
            bool same = true, inv = true;
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] != grid[0][j]) same = false;
                if (grid[i][j] == grid[0][j]) inv = false;
            }
            if (!same && !inv) return false;
        }
        return true;
    }
};

Go

func removeOnes(grid [][]int) bool {
    m, n := len(grid), len(grid[0])
    for i := 1; i < m; i++ {
        same, inv := true, true
        for j := 0; j < n; j++ {
            if grid[i][j] != grid[0][j] {
                same = false
            }
            if grid[i][j] == grid[0][j] {
                inv = false
            }
        }
        if !same && !inv {
            return false
        }
    }
    return true
}

Java

class Solution {
    public boolean removeOnes(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        for (int i = 1; i < m; ++i) {
            boolean same = true, inv = true;
            for (int j = 0; j < n; ++j) {
                if (grid[i][j] != grid[0][j]) same = false;
                if (grid[i][j] == grid[0][j]) inv = false;
            }
            if (!same && !inv) return false;
        }
        return true;
    }
}

Kotlin

class Solution {
    fun removeOnes(grid: Array<IntArray>): Boolean {
        val m = grid.size
        val n = grid[0].size
        for (i in 1 until m) {
            var same = true
            var inv = true
            for (j in 0 until n) {
                if (grid[i][j] != grid[0][j]) same = false
                if (grid[i][j] == grid[0][j]) inv = false
            }
            if (!same && !inv) return false
        }
        return true
    }
}

Python

class Solution:
    def removeOnes(self, grid: list[list[int]]) -> bool:
        m, n = len(grid), len(grid[0])
        for i in range(1, m):
            same = True
            inv = True
            for j in range(n):
                if grid[i][j] != grid[0][j]:
                    same = False
                if grid[i][j] == grid[0][j]:
                    inv = False
            if not same and not inv:
                return False
        return True

Rust

impl Solution {
    pub fn remove_ones(grid: Vec<Vec<i32>>) -> bool {
        let m = grid.len();
        let n = grid[0].len();
        for i in 1..m {
            let mut same = true;
            let mut inv = true;
            for j in 0..n {
                if grid[i][j] != grid[0][j] { same = false; }
                if grid[i][j] == grid[0][j] { inv = false; }
            }
            if !same && !inv { return false; }
        }
        true
    }
}

TypeScript

class Solution {
    removeOnes(grid: number[][]): boolean {
        const m = grid.length, n = grid[0].length;
        for (let i = 1; i < m; ++i) {
            let same = true, inv = true;
            for (let j = 0; j < n; ++j) {
                if (grid[i][j] !== grid[0][j]) same = false;
                if (grid[i][j] === grid[0][j]) inv = false;
            }
            if (!same && !inv) return false;
        }
        return true;
    }
}

Complexity

• ⏰ Time complexity: O(m * n), since we check every cell in the grid once.
• 🧺 Space complexity: O(1), as we use only a constant amount of extra space.