Remove All Ones With Row and Column Flips II
MediumUpdated: Aug 2, 2025
Practice on:
Problem
You are given a 0-indexed m x n binary matrix grid.
In one operation, you can choose any i and j that meet the following conditions:
0 <= i < m0 <= j < ngrid[i][j] == 1
and change the values of all cells in row i and column j to zero.
Return _theminimum number of operations needed to remove all _1 _' s from _grid .
Examples
Example 1:
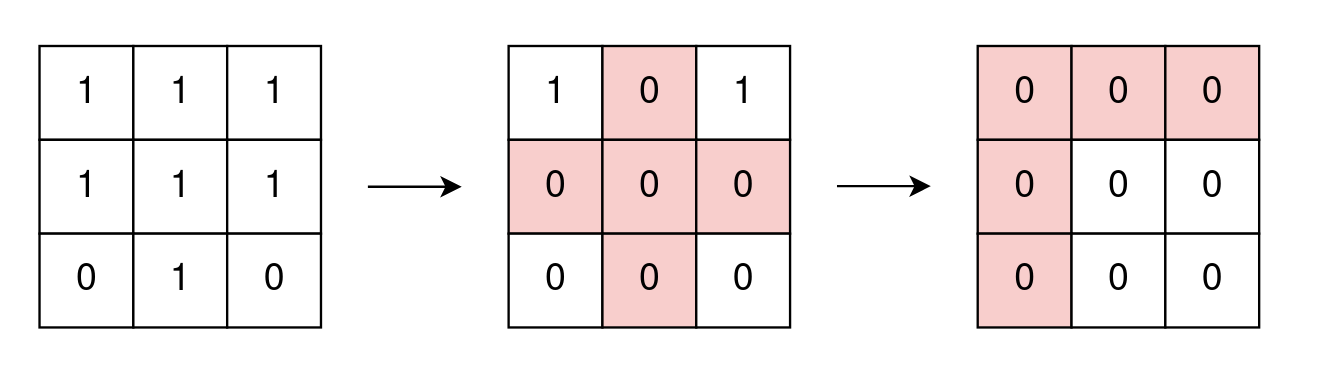
Input: grid = [[1,1,1],[1,1,1],[0,1,0]]
Output: 2
Explanation:
In the first operation, change all cell values of row 1 and column 1 to zero.
In the second operation, change all cell values of row 0 and column 0 to zero.
Example 2:
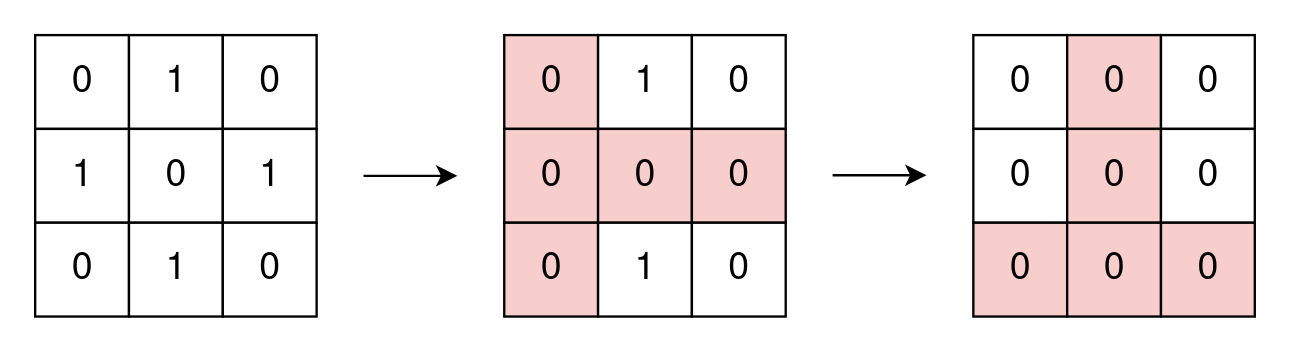
Input: grid = [[0,1,0],[1,0,1],[0,1,0]]
Output: 2
Explanation:
In the first operation, change all cell values of row 1 and column 0 to zero.
In the second operation, change all cell values of row 2 and column 1 to zero.
Note that we cannot perform an operation using row 1 and column 1 because grid[1][1] != 1.
Example 3:
Input: grid = [[0,0],[0,0]]
Output: 0
Explanation:
There are no 1's to remove so return 0.
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 151 <= m * n <= 15grid[i][j]is either0or1.
Solution
Method 1 – Bitmask BFS (State Compression)
Intuition
Since the grid is small (at most 15 cells), we can represent the entire grid as a bitmask (an integer). Each operation zeroes out a row and a column if the cell is 1, so we can use BFS to find the minimum number of operations to reach the all-zero state.
Approach
- Encode the grid as a single integer (bitmask), where each bit represents a cell.
- Use BFS to explore all possible states, starting from the initial grid.
- For each state, for every cell with 1, simulate the operation (zero out its row and column) and enqueue the new state if not visited.
- The answer is the minimum number of steps to reach the all-zero state.
- Use a set to avoid revisiting states.
Code
C++
class Solution {
public:
int removeOnes(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
int total = m * n;
int start = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j]) start |= (1 << (i * n + j));
queue<pair<int, int>> q;
unordered_set<int> vis;
q.push({start, 0});
vis.insert(start);
while (!q.empty()) {
auto [mask, step] = q.front(); q.pop();
if (mask == 0) return step;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (!(mask & (1 << (i * n + j)))) continue;
int nmask = mask;
for (int k = 0; k < n; ++k) nmask &= ~(1 << (i * n + k));
for (int k = 0; k < m; ++k) nmask &= ~(1 << (k * n + j));
if (!vis.count(nmask)) {
vis.insert(nmask);
q.push({nmask, step + 1});
}
}
}
}
return -1;
}
};
Go
func removeOnes(grid [][]int) int {
m, n := len(grid), len(grid[0])
total := m * n
start := 0
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if grid[i][j] == 1 {
start |= 1 << (i*n + j)
}
}
}
type pair struct{ mask, step int }
q := []pair{{start, 0}}
vis := map[int]bool{start: true}
for len(q) > 0 {
p := q[0]
q = q[1:]
if p.mask == 0 {
return p.step
}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
if p.mask&(1<<(i*n+j)) == 0 {
continue
}
nmask := p.mask
for k := 0; k < n; k++ {
nmask &^= 1 << (i*n + k)
}
for k := 0; k < m; k++ {
nmask &^= 1 << (k*n + j)
}
if !vis[nmask] {
vis[nmask] = true
q = append(q, pair{nmask, p.step + 1})
}
}
}
}
return -1
}
Java
import java.util.*;
class Solution {
public int removeOnes(int[][] grid) {
int m = grid.length, n = grid[0].length, total = m * n;
int start = 0;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j)
if (grid[i][j] == 1) start |= (1 << (i * n + j));
Queue<int[]> q = new LinkedList<>();
Set<Integer> vis = new HashSet<>();
q.offer(new int[]{start, 0});
vis.add(start);
while (!q.isEmpty()) {
int[] cur = q.poll();
int mask = cur[0], step = cur[1];
if (mask == 0) return step;
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if ((mask & (1 << (i * n + j))) == 0) continue;
int nmask = mask;
for (int k = 0; k < n; ++k) nmask &= ~(1 << (i * n + k));
for (int k = 0; k < m; ++k) nmask &= ~(1 << (k * n + j));
if (!vis.contains(nmask)) {
vis.add(nmask);
q.offer(new int[]{nmask, step + 1});
}
}
}
}
return -1;
}
}
Kotlin
import java.util.*
class Solution {
fun removeOnes(grid: Array<IntArray>): Int {
val m = grid.size
val n = grid[0].size
val total = m * n
var start = 0
for (i in 0 until m)
for (j in 0 until n)
if (grid[i][j] == 1) start = start or (1 shl (i * n + j))
val q: Queue<Pair<Int, Int>> = LinkedList()
val vis = mutableSetOf<Int>()
q.offer(Pair(start, 0))
vis.add(start)
while (q.isNotEmpty()) {
val (mask, step) = q.poll()
if (mask == 0) return step
for (i in 0 until m) {
for (j in 0 until n) {
if ((mask and (1 shl (i * n + j))) == 0) continue
var nmask = mask
for (k in 0 until n) nmask = nmask and (1 shl (i * n + k)).inv()
for (k in 0 until m) nmask = nmask and (1 shl (k * n + j)).inv()
if (nmask !in vis) {
vis.add(nmask)
q.offer(Pair(nmask, step + 1))
}
}
}
}
return -1
}
}
Python
from collections import deque
class Solution:
def removeOnes(self, grid: list[list[int]]) -> int:
m, n = len(grid), len(grid[0])
start = 0
for i in range(m):
for j in range(n):
if grid[i][j]:
start |= 1 << (i * n + j)
q = deque([(start, 0)])
vis = {start}
while q:
mask, step = q.popleft()
if mask == 0:
return step
for i in range(m):
for j in range(n):
if not (mask & (1 << (i * n + j))):
continue
nmask = mask
for k in range(n):
nmask &= ~(1 << (i * n + k))
for k in range(m):
nmask &= ~(1 << (k * n + j))
if nmask not in vis:
vis.add(nmask)
q.append((nmask, step + 1))
return -1
Rust
use std::collections::{VecDeque, HashSet};
impl Solution {
pub fn remove_ones(grid: Vec<Vec<i32>>) -> i32 {
let m = grid.len();
let n = grid[0].len();
let mut start = 0;
for i in 0..m {
for j in 0..n {
if grid[i][j] == 1 {
start |= 1 << (i * n + j);
}
}
}
let mut q = VecDeque::new();
let mut vis = HashSet::new();
q.push_back((start, 0));
vis.insert(start);
while let Some((mask, step)) = q.pop_front() {
if mask == 0 { return step; }
for i in 0..m {
for j in 0..n {
if mask & (1 << (i * n + j)) == 0 { continue; }
let mut nmask = mask;
for k in 0..n { nmask &= !(1 << (i * n + k)); }
for k in 0..m { nmask &= !(1 << (k * n + j)); }
if !vis.contains(&nmask) {
vis.insert(nmask);
q.push_back((nmask, step + 1));
}
}
}
}
-1
}
}
TypeScript
class Solution {
removeOnes(grid: number[][]): number {
const m = grid.length, n = grid[0].length;
let start = 0;
for (let i = 0; i < m; ++i)
for (let j = 0; j < n; ++j)
if (grid[i][j]) start |= (1 << (i * n + j));
const q: [number, number][] = [[start, 0]];
const vis = new Set<number>([start]);
while (q.length) {
const [mask, step] = q.shift()!;
if (mask === 0) return step;
for (let i = 0; i < m; ++i) {
for (let j = 0; j < n; ++j) {
if (!(mask & (1 << (i * n + j)))) continue;
let nmask = mask;
for (let k = 0; k < n; ++k) nmask &= ~(1 << (i * n + k));
for (let k = 0; k < m; ++k) nmask &= ~(1 << (k * n + j));
if (!vis.has(nmask)) {
vis.add(nmask);
q.push([nmask, step + 1]);
}
}
}
}
return -1;
}
}
Complexity
- ⏰ Time complexity:
O(2^{m*n} * m * n), since there are at most2^{m*n}states and for each state, we try up tom*noperations. - 🧺 Space complexity:
O(2^{m*n}), for the visited set and queue.