problemmediumalgorithmsleetcode-1272leetcode 1272leetcode1272

Remove Interval

MediumUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

A set of real numbers can be represented as the union of several disjoint intervals, where each interval is in the form [a, b). A real number x is in the set if one of its intervals [a, b) contains x (i.e. a <= x < b).

You are given a sorted list of disjoint intervals intervals representing a set of real numbers as described above, where intervals[i] = [ai, bi] represents the interval [ai, bi). You are also given another interval toBeRemoved.

Return the set of real numbers with the intervaltoBeRemoved removed from __intervals . In other words, return the set of real numbers such that everyx in the set is inintervals _butnot in _toBeRemoved . Your answer should be asorted list of disjoint intervals as described above.

Examples

Example 1:

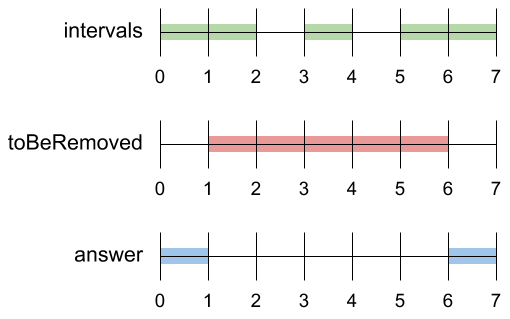
Input: intervals = [[0,2],[3,4],[5,7]], toBeRemoved = [1,6]
Output: [[0,1],[6,7]]

Example 2:

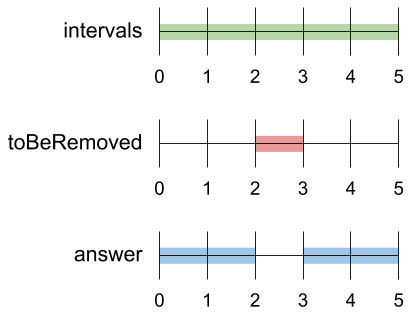
Input: intervals = [[0,5]], toBeRemoved = [2,3]
Output: [[0,2],[3,5]]

Example 3:

Input: intervals = [[-5,-4],[-3,-2],[1,2],[3,5],[8,9]], toBeRemoved = [-1,4]
Output: [[-5,-4],[-3,-2],[4,5],[8,9]]

Constraints:

  • 1 <= intervals.length <= 10^4
  • -10^9 <= ai < bi <= 10^9

Solution

Method 1 - Interval Splitting

Intuition

For each interval, if it overlaps with the interval to be removed, we split it into at most two intervals: the part before the removal and the part after. If it doesn't overlap, we keep it as is.

Approach

Iterate through each interval:

  • If the interval is completely before or after toBeRemoved, keep it as is.
  • If it overlaps, add the non-overlapping parts (if any) to the result.

Code

C++
class Solution {
public:
    vector<vector<int>> removeInterval(vector<vector<int>>& intervals, vector<int>& toBeRemoved) {
        vector<vector<int>> res;
        int remL = toBeRemoved[0], remR = toBeRemoved[1];
        for (auto& it : intervals) {
            int l = it[0], r = it[1];
            if (r <= remL || l >= remR) {
                res.push_back({l, r});
            } else {
                if (l < remL) res.push_back({l, min(r, remL)});
                if (r > remR) res.push_back({max(l, remR), r});
            }
        }
        return res;
    }
};
Go
func removeInterval(intervals [][]int, toBeRemoved []int) [][]int {
    res := [][]int{}
    remL, remR := toBeRemoved[0], toBeRemoved[1]
    for _, it := range intervals {
        l, r := it[0], it[1]
        if r <= remL || l >= remR {
            res = append(res, []int{l, r})
        } else {
            if l < remL {
                res = append(res, []int{l, min(r, remL)})
            }
            if r > remR {
                res = append(res, []int{max(l, remR), r})
            }
        }
    }
    return res
}
func min(a, b int) int { if a < b { return a }; return b }
func max(a, b int) int { if a > b { return a }; return b }
Java
class Solution {
    public List<List<Integer>> removeInterval(int[][] intervals, int[] toBeRemoved) {
        List<List<Integer>> res = new ArrayList<>();
        int remL = toBeRemoved[0], remR = toBeRemoved[1];
        for (int[] it : intervals) {
            int l = it[0], r = it[1];
            if (r <= remL || l >= remR) {
                res.add(Arrays.asList(l, r));
            } else {
                if (l < remL) res.add(Arrays.asList(l, Math.min(r, remL)));
                if (r > remR) res.add(Arrays.asList(Math.max(l, remR), r));
            }
        }
        return res;
    }
}
Kotlin
class Solution {
    fun removeInterval(intervals: Array<IntArray>, toBeRemoved: IntArray): List<List<Int>> {
        val res = mutableListOf<List<Int>>()
        val remL = toBeRemoved[0]
        val remR = toBeRemoved[1]
        for (it in intervals) {
            val l = it[0]
            val r = it[1]
            if (r <= remL || l >= remR) {
                res.add(listOf(l, r))
            } else {
                if (l < remL) res.add(listOf(l, minOf(r, remL)))
                if (r > remR) res.add(listOf(maxOf(l, remR), r))
            }
        }
        return res
    }
}
Python
from typing import List
class Solution:
    def removeInterval(self, intervals: List[List[int]], toBeRemoved: List[int]) -> List[List[int]]:
        res = []
        remL, remR = toBeRemoved
        for l, r in intervals:
            if r <= remL or l >= remR:
                res.append([l, r])
            else:
                if l < remL:
                    res.append([l, min(r, remL)])
                if r > remR:
                    res.append([max(l, remR), r])
        return res
Rust
impl Solution {
    pub fn remove_interval(intervals: Vec<Vec<i32>>, to_be_removed: Vec<i32>) -> Vec<Vec<i32>> {
        let mut res = Vec::new();
        let (rem_l, rem_r) = (to_be_removed[0], to_be_removed[1]);
        for it in intervals.iter() {
            let (l, r) = (it[0], it[1]);
            if r <= rem_l || l >= rem_r {
                res.push(vec![l, r]);
            } else {
                if l < rem_l {
                    res.push(vec![l, r.min(rem_l)]);
                }
                if r > rem_r {
                    res.push(vec![l.max(rem_r), r]);
                }
            }
        }
        res
    }
}
TypeScript
function removeInterval(intervals: number[][], toBeRemoved: number[]): number[][] {
    const res: number[][] = [];
    const [remL, remR] = toBeRemoved;
    for (const [l, r] of intervals) {
        if (r <= remL || l >= remR) {
            res.push([l, r]);
        } else {
            if (l < remL) res.push([l, Math.min(r, remL)]);
            if (r > remR) res.push([Math.max(l, remR), r]);
        }
    }
    return res;
}

Complexity

  • ⏰ Time complexity: O(n) where n is the number of intervals.
  • 🧺 Space complexity: O(n) for the result list.

Comments