Problem

Alice and Bob have an undirected graph of n nodes and three types of edges:

  • Type 1: Can be traversed by Alice only.
  • Type 2: Can be traversed by Bob only.
  • Type 3: Can be traversed by both Alice and Bob.

Given an array edges where edges[i] = [typei, ui, vi] represents a bidirectional edge of type typei between nodes ui and vi, find the maximum number of edges you can remove so that after removing the edges, the graph can still be fully traversed by both Alice and Bob. The graph is fully traversed by Alice and Bob if starting from any node, they can reach all other nodes.

Return the maximum number of edges you can remove, or return -1 if Alice and Bob cannot fully traverse the graph.

Examples

Example 1:

1
2
3
4
5

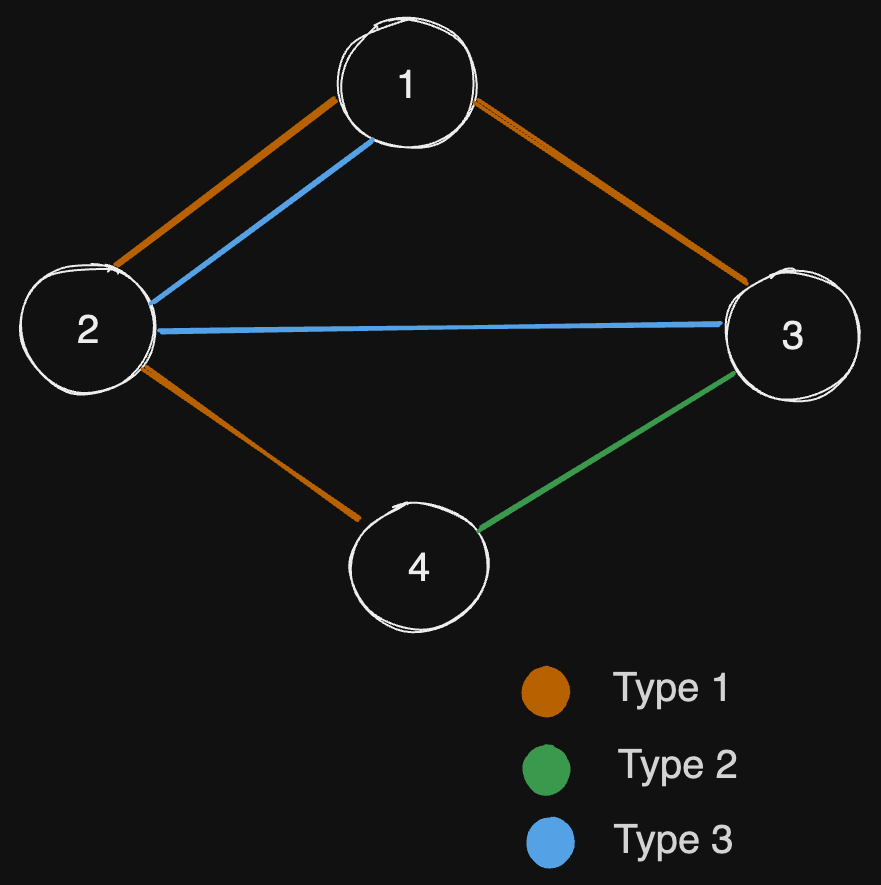
Input:
n = 4, edges =[[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]
Output:
 2
Explanation: If we remove the 2 edges [1,1,2] and [1,1,3]. The graph will still be fully traversable by Alice and Bob. Removing any additional edge will not make it so. So the maximum number of edges we can remove is 2.

Example 2:

1
2
3
4
5

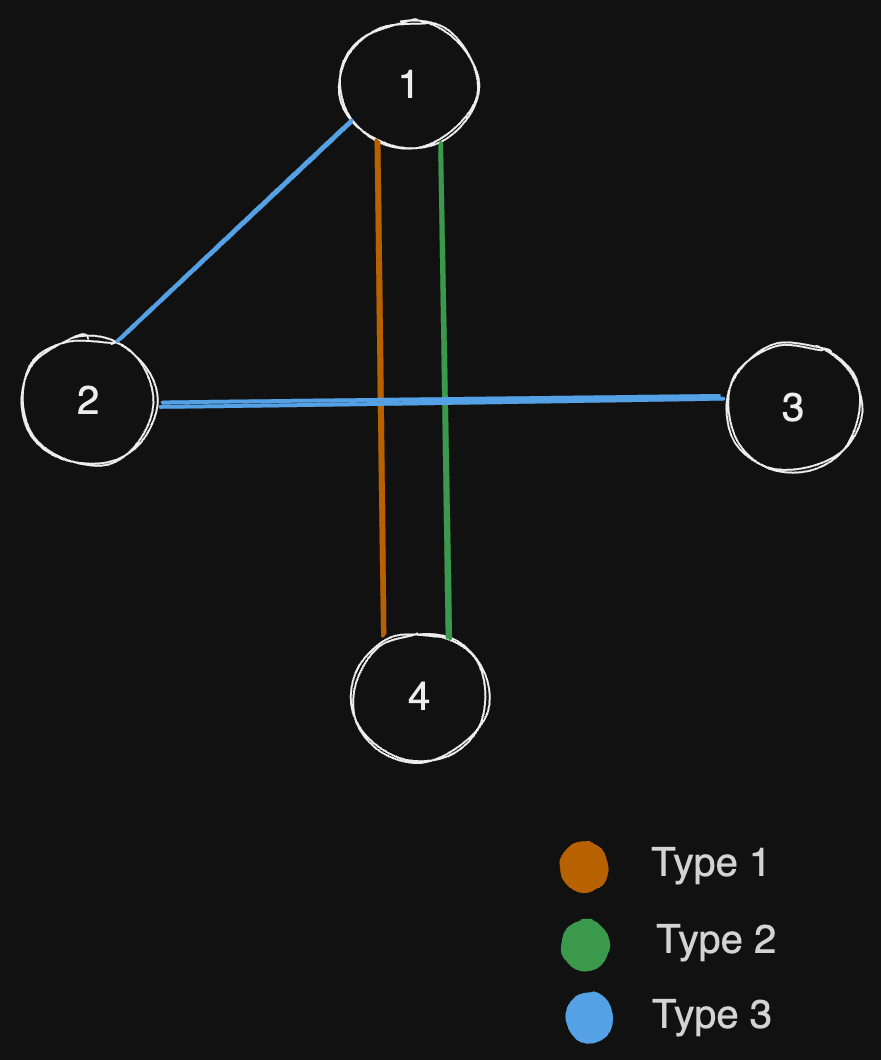
Input:
n = 4, edges =[[3,1,2],[3,2,3],[1,1,4],[2,1,4]]
Output:
 0
Explanation: Notice that removing any edge will not make the graph fully traversable by Alice and Bob.

Example 3:

1
2
3
4
5

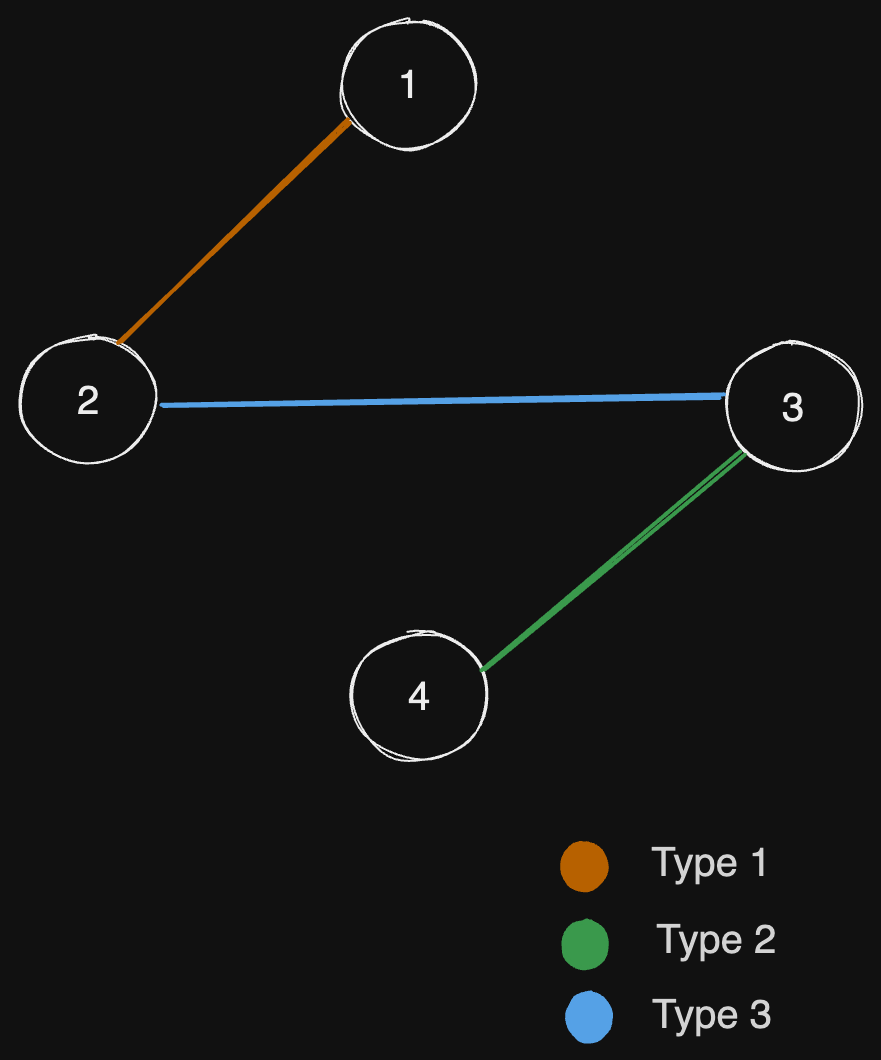
Input:
n = 4, edges =[[3,2,3],[1,1,2],[2,3,4]]
Output:
 -1
Explanation: In the current graph, Alice cannot reach node 4 from the other nodes. Likewise, Bob cannot reach 1. Therefore it's impossible to make the graph fully traversable.

Solution

This is hard problem, if we don’t know Union Find data structure, as this problem is modelled on Union Find. Look at some medium problems like Redundant Connection OR Number of Provinces before solving this problem, and understand Union Find data structure.

Method 1 - Using Union Find

The concept is to start with an empty graph for both Alice and Bob and incrementally add edges to make the graph connected.

Union-Find provides a simple solution by initially considering all nodes as separate components and merging them as edges are added.

Since some edges cater exclusively to Bob and others to Alice, we’ll use two separate Union-Find structures to manage their respective connections.

It’s crucial to prioritize type 3 edges over type 1 and type 2 edges since type 3 edges benefit both Bob and Alice simultaneously.

Steps

  1. Sort the edges based on type, in reverse order as we prefer type-3 edge, which allows both Alice and Bob to traverse.
  2. Now, build the union-find graph for both alice and bob.
    1. If we add the edge to either Alice and Bob, when doing union operation, we count addedEdges
  3. In the end, we check both alice and bob are fully connected, and return the difference between edges.length and addedEdges.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98

class Solution {
    public int maxNumEdgesToRemove(int n, int[][] edges) {
        Arrays.sort(edges, (a, b) -> b[0] - a[0]); // sort edges by type in reverse order
        
        int addedEdges = 0;
        
        UnionFind alice = new UnionFind(n);
        UnionFind bob = new UnionFind(n);
        // start adding edges
        for (int[] edge : edges) {
            int type = edge[0];
            int u = edge[1] - 1; // subtracting one, because or UF is indexed at 0
            int v = edge[2] - 1;
            
            switch (type) {
                case 3:
                    if (alice.union(u, v) | bob.union(u, v)) {
                        addedEdges++;
                    }
                    break;
                case 2:
                    if (bob.union(u, v)) {
                        addedEdges++;
                    }
                    break;
                case 1:
                    if (alice.union(u, v)) {
                        addedEdges++;
                    } 
                    break;
            }
        }
        
        return (alice.isFullyConnected() && bob.isFullyConnected()) ? edges.length - addedEdges : -1;
    }

    static class UnionFind {

		private int[] parent;

		private int[] rank;

		private int numComponents;

		public UnionFind(int n) {
			this.numComponents = n;
			makeSet();
		}

		private void makeSet() {
			rank = new int[numComponents];
			parent = new int[numComponents];

			for (int i = 0; i < parent.length; i++) {
				parent[i] = i;
				rank[i] = 0;
			}
		}

		public boolean union(int x, int y) {
			int root1 = find(x);
			int root2 = find(y);

			if (root1 == root2) {
				return false;
			}

			if (rank[root1] > rank[root2]) {
				parent[root2] = root1;
			} else {
				parent[root1] = root2;
			}

			if (rank[root1] == rank[root2]) {
				rank[root2] += 1;
			}

			numComponents--;
            return true;
		}

		public int find(int x) {
			while (parent[x] != x) {
				x = parent[x];
			}

			return x;
		}

		public int getNumComponents() {
			return numComponents;
		}

        public boolean isFullyConnected() {
            return numComponents == 1;
        }
	}
}

Complexity

  • Time: O(m log m + mα(n)), where m is number of edges, and n is number nodes.
    • As we sorted the edges, it takes O(m log m)
    • Adding an edge using union operation takes O(α(n)), where α(n) is the extremely fast inverse Ackermann function.
    • As we are adding m edges, it takes O(mα(n))
  • Space: O(n), where n is number of nodes as we store parent and rank arrays in Union Find data structure.