Remove Methods From Project

Problem

You are maintaining a project that has n methods numbered from 0 to n -1.

You are given two integers n and k, and a 2D integer array invocations, where invocations[i] = [ai, bi] indicates that method ai invokes method bi.

There is a known bug in method k. Method k, along with any method invoked by it, either directly or indirectly , are considered suspicious and we aim to remove them.

A group of methods can only be removed if no method outside the group invokes any methods within it.

Return an array containing all the remaining methods after removing all the suspicious methods. You may return the answer in any order. If it is not possible to remove all the suspicious methods, none should be removed.

Examples

Example 1

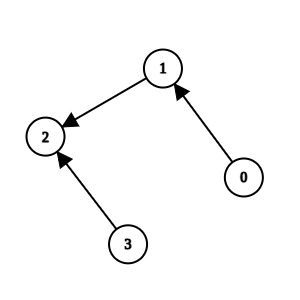
Input: n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]

Output: [0,1,2,3]

Explanation:
Method 2 and method 1 are suspicious, but they are directly invoked by methods 3 and 0, which are not suspicious. We return all elements without removing anything.

Example 2

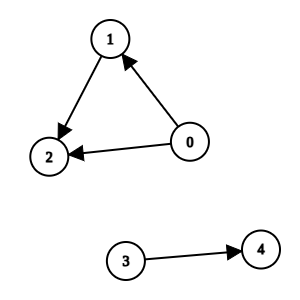
Input: n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]
Output: [3,4]
Explanation:
Methods 0, 1, and 2 are suspicious and they are not directly invoked by any other method. We can remove them.

Example 3

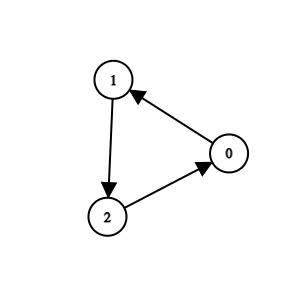
Input: n = 3, k = 2, invocations = [[1,2],[0,1],[2,0]]
Output: []
Explanation:
All methods are suspicious. We can remove them.

Constraints

• 1 <= n <= 10^5
• 0 <= k <= n - 1
• 0 <= invocations.length <= 2 * 10^5
• invocations[i] == [ai, bi]
• 0 <= ai, bi <= n - 1
• ai != bi
• invocations[i] != invocations[j]

Solution

Method 1 - BFS/DFS for Suspicious Group and In-Degree Check

Intuition

The core problem is identifying suspicious methods (those reachable from the buggy method k) and determining if they can be safely removed. A suspicious method can only be removed if no non-suspicious method invokes it. We need to build both forward and reverse dependency graphs to check for external dependencies into the suspicious group.

Approach

1. Build adjacency lists for both forward invocations and reverse invocations (who calls whom vs. who is called by whom).
2. Use DFS from method k in the forward graph to identify all suspicious methods (directly or indirectly invoked by k).
3. Use DFS from each suspicious method in the reverse graph to find all methods that can reach suspicious methods.
4. If any method that can reach suspicious methods is itself not suspicious, then external dependencies exist and removal is impossible.
5. If no external dependencies exist, return all non-suspicious methods; otherwise, return all methods unchanged.

Code

C++

#include <vector>
#include <numeric>
using namespace std;

class Solution {
private:
    void dfs(int node, vector<bool>& visited, const vector<vector<int>>& adj) {
        visited[node] = true;
        for (int neighbor : adj[node]) {
            if (!visited[neighbor]) {
                dfs(neighbor, visited, adj);
            }
        }
    }

public:
    vector<int> remainingMethods(int n, int k, vector<vector<int>>& invocations) {
        // Build forward and reverse adjacency lists
        vector<vector<int>> adj(n), reverseAdj(n);
        for (const auto& invocation : invocations) {
            adj[invocation[0]].push_back(invocation[1]);
            reverseAdj[invocation[1]].push_back(invocation[0]);
        }
        
        // Find all suspicious methods (reachable from k)
        vector<bool> suspicious(n, false);
        dfs(k, suspicious, adj);
        
        // Find all methods that can reach suspicious methods
        vector<bool> canReachSuspicious(n, false);
        for (int i = 0; i < n; ++i) {
            if (suspicious[i] && !canReachSuspicious[i]) {
                dfs(i, canReachSuspicious, reverseAdj);
            }
        }
        
        // Check if any non-suspicious method can reach suspicious methods
        for (int i = 0; i < n; ++i) {
            if (canReachSuspicious[i] && !suspicious[i]) {
                // External dependency found, cannot remove suspicious methods
                vector<int> allMethods(n);
                iota(allMethods.begin(), allMethods.end(), 0);
                return allMethods;
            }
        }
        
        // No external dependencies, return non-suspicious methods
        vector<int> result;
        for (int i = 0; i < n; ++i) {
            if (!suspicious[i]) {
                result.push_back(i);
            }
        }
        return result;
    }
};

Go

func remainingMethods(n int, k int, invocations [][]int) []int {
    // Build forward and reverse adjacency lists
    adj := make([][]int, n)
    reverseAdj := make([][]int, n)
    for _, invocation := range invocations {
        adj[invocation[0]] = append(adj[invocation[0]], invocation[1])
        reverseAdj[invocation[1]] = append(reverseAdj[invocation[1]], invocation[0])
    }
    
    // DFS helper function
    var dfs func(int, []bool, [][]int)
    dfs = func(node int, visited []bool, graph [][]int) {
        visited[node] = true
        for _, neighbor := range graph[node] {
            if !visited[neighbor] {
                dfs(neighbor, visited, graph)
            }
        }
    }
    
    // Find all suspicious methods (reachable from k)
    suspicious := make([]bool, n)
    dfs(k, suspicious, adj)
    
    // Find all methods that can reach suspicious methods
    canReachSuspicious := make([]bool, n)
    for i := 0; i < n; i++ {
        if suspicious[i] && !canReachSuspicious[i] {
            dfs(i, canReachSuspicious, reverseAdj)
        }
    }
    
    // Check if any non-suspicious method can reach suspicious methods
    for i := 0; i < n; i++ {
        if canReachSuspicious[i] && !suspicious[i] {
            // External dependency found, return all methods
            allMethods := make([]int, n)
            for j := 0; j < n; j++ {
                allMethods[j] = j
            }
            return allMethods
        }
    }
    
    // No external dependencies, return non-suspicious methods
    var result []int
    for i := 0; i < n; i++ {
        if !suspicious[i] {
            result = append(result, i)
        }
    }
    return result
}

Java

import java.util.*;

class Solution {
    private void dfs(int node, boolean[] visited, List<List<Integer>> adj) {
        visited[node] = true;
        for (int neighbor : adj.get(node)) {
            if (!visited[neighbor]) {
                dfs(neighbor, visited, adj);
            }
        }
    }
    
    public List<Integer> remainingMethods(int n, int k, int[][] invocations) {
        // Build forward and reverse adjacency lists
        List<List<Integer>> adj = new ArrayList<>();
        List<List<Integer>> reverseAdj = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            adj.add(new ArrayList<>());
            reverseAdj.add(new ArrayList<>());
        }
        
        for (int[] invocation : invocations) {
            adj.get(invocation[0]).add(invocation[1]);
            reverseAdj.get(invocation[1]).add(invocation[0]);
        }
        
        // Find all suspicious methods (reachable from k)
        boolean[] suspicious = new boolean[n];
        dfs(k, suspicious, adj);
        
        // Find all methods that can reach suspicious methods
        boolean[] canReachSuspicious = new boolean[n];
        for (int i = 0; i < n; i++) {
            if (suspicious[i] && !canReachSuspicious[i]) {
                dfs(i, canReachSuspicious, reverseAdj);
            }
        }
        
        // Check if any non-suspicious method can reach suspicious methods
        for (int i = 0; i < n; i++) {
            if (canReachSuspicious[i] && !suspicious[i]) {
                // External dependency found, return all methods
                List<Integer> allMethods = new ArrayList<>();
                for (int j = 0; j < n; j++) {
                    allMethods.add(j);
                }
                return allMethods;
            }
        }
        
        // No external dependencies, return non-suspicious methods
        List<Integer> result = new ArrayList<>();
        for (int i = 0; i < n; i++) {
            if (!suspicious[i]) {
                result.add(i);
            }
        }
        return result;
    }
}

Kotlin

class Solution {
    private fun dfs(node: Int, visited: BooleanArray, adj: Array<MutableList<Int>>) {
        visited[node] = true
        for (neighbor in adj[node]) {
            if (!visited[neighbor]) {
                dfs(neighbor, visited, adj)
            }
        }
    }
    
    fun remainingMethods(n: Int, k: Int, invocations: Array<IntArray>): List<Int> {
        // Build forward and reverse adjacency lists
        val adj = Array(n) { mutableListOf<Int>() }
        val reverseAdj = Array(n) { mutableListOf<Int>() }
        
        for (invocation in invocations) {
            adj[invocation[0]].add(invocation[1])
            reverseAdj[invocation[1]].add(invocation[0])
        }
        
        // Find all suspicious methods (reachable from k)
        val suspicious = BooleanArray(n)
        dfs(k, suspicious, adj)
        
        // Find all methods that can reach suspicious methods
        val canReachSuspicious = BooleanArray(n)
        for (i in 0 until n) {
            if (suspicious[i] && !canReachSuspicious[i]) {
                dfs(i, canReachSuspicious, reverseAdj)
            }
        }
        
        // Check if any non-suspicious method can reach suspicious methods
        for (i in 0 until n) {
            if (canReachSuspicious[i] && !suspicious[i]) {
                // External dependency found, return all methods
                return (0 until n).toList()
            }
        }
        
        // No external dependencies, return non-suspicious methods
        return (0 until n).filter { !suspicious[it] }
    }
}

Python

def removeMethods(n, k, invocations):
    from collections import deque
    g = [[] for _ in range(n)]
    for a, b in invocations:
        g[a].append(b)
    suspicious = [False] * n
    q = deque([k])
    suspicious[k] = True
    while q:
        u = q.popleft()
        for v in g[u]:
            if not suspicious[v]:
                suspicious[v] = True
                q.append(v)
    for a, b in invocations:
        if not suspicious[a] and suspicious[b]:
            return list(range(n))
##### Rust

```rust
impl Solution {
    fn dfs(node: usize, visited: &mut Vec<bool>, adj: &Vec<Vec<usize>>) {
        visited[node] = true;
        for &neighbor in &adj[node] {
            if !visited[neighbor] {
                Self::dfs(neighbor, visited, adj);
            }
        }
    }
    
    pub fn remaining_methods(n: i32, k: i32, invocations: Vec<Vec<i32>>) -> Vec<i32> {
        let n = n as usize;
        let k = k as usize;
        
        // Build forward and reverse adjacency lists
        let mut adj = vec![Vec::new(); n];
        let mut reverse_adj = vec![Vec::new(); n];
        
        for invocation in &invocations {
            let from = invocation[0] as usize;
            let to = invocation[1] as usize;
            adj[from].push(to);
            reverse_adj[to].push(from);
        }
        
        // Find all suspicious methods (reachable from k)
        let mut suspicious = vec![false; n];
        Self::dfs(k, &mut suspicious, &adj);
        
        // Find all methods that can reach suspicious methods
        let mut can_reach_suspicious = vec![false; n];
        for i in 0..n {
            if suspicious[i] && !can_reach_suspicious[i] {
                Self::dfs(i, &mut can_reach_suspicious, &reverse_adj);
            }
        }
        
        // Check if any non-suspicious method can reach suspicious methods
        for i in 0..n {
            if can_reach_suspicious[i] && !suspicious[i] {
                // External dependency found, return all methods
                return (0..n as i32).collect();
            }
        }
        
        // No external dependencies, return non-suspicious methods
        (0..n as i32).filter(|&i| !suspicious[i as usize]).collect()
    }
}

TypeScript

function remainingMethods(n: number, k: number, invocations: number[][]): number[] {
    // Build forward and reverse adjacency lists
    const adj: number[][] = Array.from({ length: n }, () => []);
    const reverseAdj: number[][] = Array.from({ length: n }, () => []);
    
    for (const [from, to] of invocations) {
        adj[from].push(to);
        reverseAdj[to].push(from);
    }
    
    // DFS helper function
    const dfs = (node: number, visited: boolean[], graph: number[][]): void => {
        visited[node] = true;
        for (const neighbor of graph[node]) {
            if (!visited[neighbor]) {
                dfs(neighbor, visited, graph);
            }
        }
    };
    
    // Find all suspicious methods (reachable from k)
    const suspicious = Array(n).fill(false);
    dfs(k, suspicious, adj);
    
    // Find all methods that can reach suspicious methods
    const canReachSuspicious = Array(n).fill(false);
    for (let i = 0; i < n; i++) {
        if (suspicious[i] && !canReachSuspicious[i]) {
            dfs(i, canReachSuspicious, reverseAdj);
        }
    }
    
    // Check if any non-suspicious method can reach suspicious methods
    for (let i = 0; i < n; i++) {
        if (canReachSuspicious[i] && !suspicious[i]) {
            // External dependency found, return all methods
            return Array.from({ length: n }, (_, i) => i);
        }
    }
    
    // No external dependencies, return non-suspicious methods
    return Array.from({ length: n }, (_, i) => i).filter(i => !suspicious[i]);
}

Complexity

• ⏰ Time complexity: O(n + e), where n is the number of methods and e is the number of invocations. Each node and edge is visited at most twice (once in forward DFS to find suspicious methods, once in reverse DFS to check external dependencies).
• 🧺 Space complexity: O(n + e), for storing the forward and reverse adjacency lists plus the visited arrays.