Reschedule Meetings for Maximum Free Time I

Problem

You are given an integer eventTime denoting the duration of an event, where the event occurs from time t = 0 to time t = eventTime.

You are also given two integer arrays startTime and endTime, each of length n. These represent the start and end time of n non-overlapping meetings, where the ith meeting occurs during the time [startTime[i], endTime[i]].

You can reschedule at most k meetings by moving their start time while maintaining the same duration , to maximize the longest continuous period of free time during the event.

The relative order of all the meetings should stay the same and they should remain non-overlapping.

Return the maximum amount of free time possible after rearranging the meetings.

Note that the meetings can not be rescheduled to a time outside the event.

Examples

Example 1

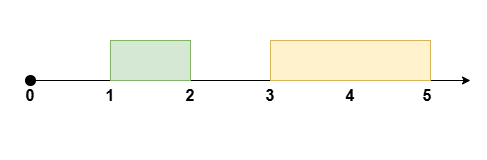
Input: eventTime = 5, k = 1, startTime = [1,3], endTime = [2,5]
Output: 2
Explanation:
Reschedule the meeting at `[1, 2]` to `[2, 3]`, leaving no meetings during the time `[0, 2]`.

Example 2

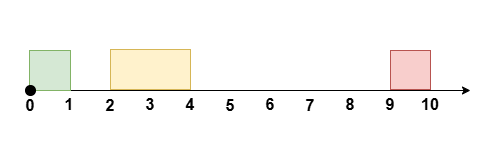
Input: eventTime = 10, k = 1, startTime = [0,2,9], endTime = [1,4,10]
Output: 6
Explanation:
Reschedule the meeting at `[2, 4]` to `[1, 3]`, leaving no meetings during the time `[3, 9]`.

Example 3

Input: eventTime = 5, k = 2, startTime = [0,1,2,3,4], endTime =
[1,2,3,4,5]
Output: 0
Explanation:
There is no time during the event not occupied by meetings.

Constraints

• 1 <= eventTime <= 10^9
• n == startTime.length == endTime.length
• 2 <= n <= 10^5
• 1 <= k <= n
• 0 <= startTime[i] < endTime[i] <= eventTime
• endTime[i] <= startTime[i + 1] where i lies in the range [0, n - 2].

Solution

Method 1 – Sliding Window on Gaps

Intuition

The free time is the gap between meetings. By rescheduling up to k meetings, we can "merge" up to k gaps, maximizing the largest continuous free time. This is a classic sliding window of size n-k+1 over the gaps.

Approach

1. Compute all gaps between meetings, including before the first and after the last meeting.
2. The answer is the maximum sum of any (k+1) consecutive gaps (i.e., after merging k gaps).

Code

C++

#include <vector>
using namespace std;
class Solution {
public:
    int maxFreeTime(int eventTime, int k, vector<int>& startTime, vector<int>& endTime) {
        int n = startTime.size();
        vector<int> gaps(n + 1);
        gaps[0] = startTime[0] - 0;
        for (int i = 1; i < n; ++i) {
            gaps[i] = startTime[i] - endTime[i - 1];
        }
        gaps[n] = eventTime - endTime[n - 1];
        int window = k + 1;
        int curr = 0, maxSum = 0;
        for (int i = 0; i < window; ++i) curr += gaps[i];
        maxSum = curr;
        for (int i = window; i < gaps.size(); ++i) {
            curr += gaps[i] - gaps[i - window];
            maxSum = max(maxSum, curr);
        }
        return maxSum;
    }
};

Go

func maxFreeTime(eventTime int, k int, startTime []int, endTime []int) int {
    n := len(startTime)
    gaps := make([]int, n+1)
    gaps[0] = startTime[0] - 0
    for i := 1; i < n; i++ {
        gaps[i] = startTime[i] - endTime[i-1]
    }
    gaps[n] = eventTime - endTime[n-1]
    window := k + 1
    curr, maxSum := 0, 0
    for i := 0; i < window; i++ {
        curr += gaps[i]
    }
    maxSum = curr
    for i := window; i < len(gaps); i++ {
        curr += gaps[i] - gaps[i-window]
        if curr > maxSum {
            maxSum = curr
        }
    }
    return maxSum
}

Java

class Solution {
    public int maxFreeTime(int eventTime, int k, int[] startTime, int[] endTime) {
        int n = startTime.length;
        int[] gaps = new int[n + 1];
        // Before first meeting
        gaps[0] = startTime[0] - 0;
        // Between meetings
        for (int i = 1; i < n; i++) {
            gaps[i] = startTime[i] - endTime[i - 1];
        }
        // After last meeting
        gaps[n] = eventTime - endTime[n - 1];
        int window = k + 1;
        int curr = 0;
        for (int i = 0; i < window; i++) curr += gaps[i];
        int maxSum = curr;
        for (int i = window; i < gaps.length; i++) {
            curr += gaps[i] - gaps[i - window];
            maxSum = Math.max(maxSum, curr);
        }
        return maxSum;
    }
}

Kotlin

fun maxFreeTime(eventTime: Int, k: Int, startTime: IntArray, endTime: IntArray): Int {
    val n = startTime.size
    val gaps = IntArray(n + 1)
    gaps[0] = startTime[0] - 0
    for (i in 1 until n) {
        gaps[i] = startTime[i] - endTime[i - 1]
    }
    gaps[n] = eventTime - endTime[n - 1]
    val window = k + 1
    var curr = 0
    for (i in 0 until window) curr += gaps[i]
    var maxSum = curr
    for (i in window until gaps.size) {
        curr += gaps[i] - gaps[i - window]
        maxSum = maxOf(maxSum, curr)
    }
    return maxSum
}

Python

def maxFreeTime(eventTime, k, startTime, endTime):
    n = len(startTime)
    # Compute all gaps
    gaps = []
    # Before first meeting
    gaps.append(startTime[0] - 0)
    # Between meetings
    for i in range(1, n):
        gaps.append(startTime[i] - endTime[i-1])
    # After last meeting
    gaps.append(eventTime - endTime[-1])
    # Sliding window of size k+1
    window = k + 1
    max_sum = curr = sum(gaps[:window])
    for i in range(window, len(gaps)):
        curr += gaps[i] - gaps[i-window]
        max_sum = max(max_sum, curr)
    return max_sum

Rust

pub fn max_free_time(event_time: i32, k: i32, start_time: Vec<i32>, end_time: Vec<i32>) -> i32 {
    let n = start_time.len();
    let mut gaps = vec![0; n + 1];
    gaps[0] = start_time[0];
    for i in 1..n {
        gaps[i] = start_time[i] - end_time[i - 1];
    }
    gaps[n] = event_time - end_time[n - 1];
    let window = (k + 1) as usize;
    let mut curr: i32 = gaps[..window].iter().sum();
    let mut max_sum = curr;
    for i in window..gaps.len() {
        curr += gaps[i] - gaps[i - window];
        if curr > max_sum {
            max_sum = curr;
        }
    }
    max_sum
}

TypeScript

function maxFreeTime(eventTime: number, k: number, startTime: number[], endTime: number[]): number {
    const n = startTime.length;
    const gaps: number[] = new Array(n + 1);
    gaps[0] = startTime[0] - 0;
    for (let i = 1; i < n; i++) {
        gaps[i] = startTime[i] - endTime[i - 1];
    }
    gaps[n] = eventTime - endTime[n - 1];
    const window = k + 1;
    let curr = 0;
    for (let i = 0; i < window; i++) curr += gaps[i];
    let maxSum = curr;
    for (let i = window; i < gaps.length; i++) {
        curr += gaps[i] - gaps[i - window];
        maxSum = Math.max(maxSum, curr);
    }
    return maxSum;
}

Complexity

• ⏰ Time complexity: O(n) — One pass to compute gaps, one pass for sliding window.
• 🧺 Space complexity: O(n) — For the gaps array.