Problem

You are given an integer eventTime denoting the duration of an event. You are also given two integer arrays startTime and endTime, each of length n.

These represent the start and end times of n non-overlapping meetings that occur during the event between time t = 0 and time t = eventTime, where the ith meeting occurs during the time [startTime[i], endTime[i]].

You can reschedule at most one meeting by moving its start time while maintaining the same duration , such that the meetings remain non-overlapping, to maximize the longest continuous period of free time during the event.

Return the maximum amount of free time possible after rearranging the meetings.

Note that the meetings can not be rescheduled to a time outside the event and they should remain non-overlapping.

Note: In this version , it is valid for the relative ordering of the meetings to change after rescheduling one meeting.

Examples

Example 1

1
2
3
4
5

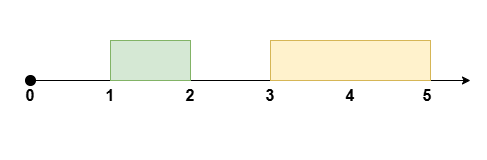
Input: eventTime = 5, startTime = [1,3], endTime = [2,5]
Output: 2
Explanation:
Reschedule the meeting at `[1, 2]` to `[2, 3]`, leaving no meetings during the
time `[0, 2]`.

Example 2

1
2
3
4
5

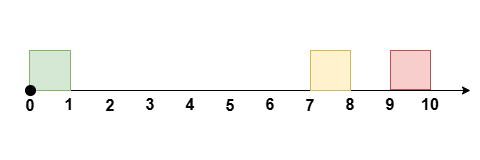
Input: eventTime = 10, startTime = [0,7,9], endTime = [1,8,10]
Output: 7
Explanation:
Reschedule the meeting at `[0, 1]` to `[8, 9]`, leaving no meetings during the
time `[0, 7]`.

Example 3

1
2
3
4
5

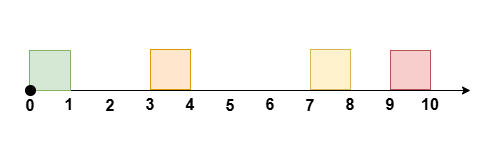
Input: eventTime = 10, startTime = [0,3,7,9], endTime = [1,4,8,10]
Output: 6
Explanation:
Reschedule the meeting at `[3, 4]` to `[8, 9]`, leaving no meetings during the
time `[1, 7]`.

Example 4

1
2
3
4

Input: eventTime = 5, startTime = [0,1,2,3,4], endTime = [1,2,3,4,5]
Output: 0
Explanation:
There is no time during the event not occupied by meetings.

Constraints

  • 1 <= eventTime <= 10^9
  • n == startTime.length == endTime.length
  • 2 <= n <= 10^5
  • 0 <= startTime[i] < endTime[i] <= eventTime
  • endTime[i] <= startTime[i + 1] where i lies in the range [0, n - 2].

Solution

Method 1 – Greedy Gap Maximization

Intuition

To maximize the longest free time, we can try moving each meeting to every possible valid position (without overlap and within event bounds), and for each configuration, calculate the maximum free gap. Since the number of meetings is small, this brute-force approach is feasible.

Approach

  1. For each meeting, try moving it to every possible valid position:
    • Remove the meeting from the list.
    • For every possible start time (from 0 to eventTime - duration), insert the meeting at that position.
    • Merge and sort all meetings, check for overlaps.
    • If valid, compute all free gaps and track the maximum.
  2. Also consider the case where no meeting is moved.
  3. Return the largest free gap found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
public:
    int maxFreeTime(int eventTime, vector<int>& s, vector<int>& e) {
        int n = s.size(), ans = 0;
        vector<pair<int,int>> mt(n);
        for(int i=0;i<n;++i) mt[i]={s[i],e[i]};
        auto getMaxGap = [&](vector<pair<int,int>>& arr) {
            sort(arr.begin(), arr.end());
            int mx = arr[0].first;
            for(int i=1;i<arr.size();++i)
                mx = max(mx, arr[i].first-arr[i-1].second);
            mx = max(mx, eventTime-arr.back().second);
            return mx;
        };
        ans = getMaxGap(mt);
        for(int i=0;i<n;++i) {
            int dur = e[i]-s[i];
            vector<pair<int,int>> rest;
            for(int j=0;j<n;++j) if(i!=j) rest.push_back({s[j],e[j]});
            for(int st=0;st<=eventTime-dur;++st) {
                pair<int,int> moved = {st,st+dur};
                vector<pair<int,int>> arr = rest;
                arr.push_back(moved);
                sort(arr.begin(), arr.end());
                bool ok = true;
                for(int k=1;k<arr.size();++k) if(arr[k].first<arr[k-1].second) ok=false;
                if(ok) ans = max(ans, getMaxGap(arr));
            }
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

func maxFreeTime(eventTime int, s []int, e []int) int {
    n, ans := len(s), 0
    mt := make([][2]int, n)
    for i := 0; i < n; i++ {
        mt[i] = [2]int{s[i], e[i]}
    }
    getMaxGap := func(arr [][2]int) int {
        sort.Slice(arr, func(i, j int) bool { return arr[i][0] < arr[j][0] })
        mx := arr[0][0]
        for i := 1; i < len(arr); i++ {
            if arr[i][0]-arr[i-1][1] > mx {
                mx = arr[i][0] - arr[i-1][1]
            }
        }
        if eventTime-arr[len(arr)-1][1] > mx {
            mx = eventTime - arr[len(arr)-1][1]
        }
        return mx
    }
    ans = getMaxGap(mt)
    for i := 0; i < n; i++ {
        dur := e[i] - s[i]
        rest := make([][2]int, 0, n-1)
        for j := 0; j < n; j++ {
            if i != j {
                rest = append(rest, [2]int{s[j], e[j]})
            }
        }
        for st := 0; st <= eventTime-dur; st++ {
            moved := [2]int{st, st + dur}
            arr := append([][2]int{}, rest...)
            arr = append(arr, moved)
            sort.Slice(arr, func(i, j int) bool { return arr[i][0] < arr[j][0] })
            ok := true
            for k := 1; k < len(arr); k++ {
                if arr[k][0] < arr[k-1][1] {
                    ok = false
                    break
                }
            }
            if ok {
                g := getMaxGap(arr)
                if g > ans {
                    ans = g
                }
            }
        }
    }
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

class Solution {
    public int maxFreeTime(int eventTime, int[] s, int[] e) {
        int n = s.length, ans = 0;
        int[][] mt = new int[n][2];
        for(int i=0;i<n;++i) mt[i]=new int[]{s[i],e[i]};
        java.util.Arrays.sort(mt, java.util.Comparator.comparingInt(a->a[0]));
        ans = getMaxGap(mt, eventTime);
        for(int i=0;i<n;++i) {
            int dur = e[i]-s[i];
            int[][] rest = new int[n-1][2];
            int idx=0;
            for(int j=0;j<n;++j) if(i!=j) rest[idx++]=new int[]{s[j],e[j]};
            for(int st=0;st<=eventTime-dur;++st) {
                int[][] arr = new int[n][2];
                for(int k=0;k<n-1;++k) arr[k]=rest[k];
                arr[n-1]=new int[]{st,st+dur};
                java.util.Arrays.sort(arr, java.util.Comparator.comparingInt(a->a[0]));
                boolean ok=true;
                for(int k=1;k<n;++k) if(arr[k][0]<arr[k-1][1]) ok=false;
                if(ok) ans=Math.max(ans, getMaxGap(arr, eventTime));
            }
        }
        return ans;
    }
    private int getMaxGap(int[][] arr, int eventTime) {
        int mx = arr[0][0];
        for(int i=1;i<arr.length;++i)
            mx = Math.max(mx, arr[i][0]-arr[i-1][1]);
        mx = Math.max(mx, eventTime-arr[arr.length-1][1]);
        return mx;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

class Solution {
    fun maxFreeTime(eventTime: Int, s: IntArray, e: IntArray): Int {
        val n = s.size
        var ans = 0
        val mt = Array(n) { i -> intArrayOf(s[i], e[i]) }
        fun getMaxGap(arr: Array<IntArray>): Int {
            arr.sortBy { it[0] }
            var mx = arr[0][0]
            for (i in 1 until arr.size) mx = maxOf(mx, arr[i][0] - arr[i-1][1])
            mx = maxOf(mx, eventTime - arr.last()[1])
            return mx
        }
        ans = getMaxGap(mt.copyOf())
        for (i in 0 until n) {
            val dur = e[i] - s[i]
            val rest = Array(n-1) { j -> if (j < i) intArrayOf(s[j], e[j]) else intArrayOf(s[j+1], e[j+1]) }
            for (st in 0..eventTime-dur) {
                val arr = rest.copyOf() + arrayOf(intArrayOf(st, st+dur))
                arr.sortBy { it[0] }
                var ok = true
                for (k in 1 until arr.size) if (arr[k][0] < arr[k-1][1]) ok = false
                if (ok) ans = maxOf(ans, getMaxGap(arr))
            }
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Solution:
    def maxFreeTime(self, eventTime: int, s: list[int], e: list[int]) -> int:
        n = len(s)
        mt = [(s[i], e[i]) for i in range(n)]
        def getMaxGap(arr: list[tuple[int,int]]) -> int:
            arr = sorted(arr)
            mx = arr[0][0]
            for i in range(1, len(arr)):
                mx = max(mx, arr[i][0] - arr[i-1][1])
            mx = max(mx, eventTime - arr[-1][1])
            return mx
        ans = getMaxGap(mt)
        for i in range(n):
            dur = e[i] - s[i]
            rest = [mt[j] for j in range(n) if j != i]
            for st in range(eventTime - dur + 1):
                arr = rest + [(st, st+dur)]
                arr.sort()
                ok = all(arr[k][0] >= arr[k-1][1] for k in range(1, n))
                if ok:
                    ans = max(ans, getMaxGap(arr))
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

impl Solution {
    pub fn max_free_time(event_time: i32, s: Vec<i32>, e: Vec<i32>) -> i32 {
        let n = s.len();
        let mut mt: Vec<(i32,i32)> = (0..n).map(|i| (s[i],e[i])).collect();
        let get_max_gap = |arr: &mut Vec<(i32,i32)>| -> i32 {
            arr.sort();
            let mut mx = arr[0].0;
            for i in 1..arr.len() {
                mx = mx.max(arr[i].0 - arr[i-1].1);
            }
            mx = mx.max(event_time - arr[arr.len()-1].1);
            mx
        };
        let mut ans = get_max_gap(&mut mt.clone());
        for i in 0..n {
            let dur = e[i] - s[i];
            let mut rest: Vec<(i32,i32)> = (0..n).filter(|&j| j!=i).map(|j| (s[j],e[j])).collect();
            for st in 0..=event_time-dur {
                let mut arr = rest.clone();
                arr.push((st,st+dur));
                arr.sort();
                let mut ok = true;
                for k in 1..arr.len() {
                    if arr[k].0 < arr[k-1].1 { ok = false; break; }
                }
                if ok {
                    let g = get_max_gap(&mut arr);
                    if g > ans { ans = g; }
                }
            }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class Solution {
    maxFreeTime(eventTime: number, s: number[], e: number[]): number {
        const n = s.length;
        const mt: [number,number][] = s.map((v,i)=>[s[i],e[i]]);
        function getMaxGap(arr: [number,number][]): number {
            arr = arr.slice().sort((a,b)=>a[0]-b[0]);
            let mx = arr[0][0];
            for(let i=1;i<arr.length;++i)
                mx = Math.max(mx, arr[i][0]-arr[i-1][1]);
            mx = Math.max(mx, eventTime-arr[arr.length-1][1]);
            return mx;
        }
        let ans = getMaxGap(mt);
        for(let i=0;i<n;++i) {
            const dur = e[i]-s[i];
            const rest = mt.filter((_,j)=>j!==i);
            for(let st=0;st<=eventTime-dur;++st) {
                const arr = rest.concat([[st,st+dur]]).sort((a,b)=>a[0]-b[0]);
                let ok = true;
                for(let k=1;k<arr.length;++k) if(arr[k][0]<arr[k-1][1]) ok=false;
                if(ok) ans = Math.max(ans, getMaxGap(arr));
            }
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n^3 * T) where n is the number of meetings and T is eventTime. For each meeting, we try all possible new positions and check validity and compute gaps.
  • 🧺 Space complexity: O(n) for storing meeting intervals and temporary arrays.

Method 2 – Optimal Merge of Free Intervals

Intuition

Instead of brute-forcing all possible positions, we can analyze the structure of the free intervals between meetings. For each meeting, there are two main ways to move it to maximize the free time:

  • If a meeting can be shifted into a non-adjacent free slot (not touching its immediate neighbors), it can create a new free interval equal to the sum of its own duration and the two adjacent free intervals.
  • Otherwise, moving the meeting merges the two adjacent free intervals into one, minus the duration of the meeting itself.

By precomputing which meetings can be shifted into such slots, we can efficiently determine the maximum possible free interval after moving any meeting.

Approach

  1. For each meeting, check if it can be moved into a non-adjacent free slot on the left or right by traversing from both directions and recording the maximum non-adjacent free slot seen so far.
  2. For each meeting, calculate the left and right boundaries (end of previous meeting and start of next meeting).
  3. If the meeting can be moved into a non-adjacent slot, the new free interval is right - left.
  4. Otherwise, the new free interval is right - left - (endTime[i] - startTime[i]).
  5. Return the maximum value found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    int maxFreeTime(int eventTime, vector<int>& s, vector<int>& e) {
        int n = s.size();
        vector<bool> q(n, false);
        for(int i=0, t1=0, t2=0; i<n; ++i) {
            if(e[i]-s[i]<=t1) q[i]=true;
            t1 = max(t1, s[i]-(i==0?0:e[i-1]));
            if(e[n-i-1]-s[n-i-1]<=t2) q[n-i-1]=true;
            t2 = max(t2, (i==0?eventTime:s[n-i])-e[n-i-1]);
        }
        int ans=0;
        for(int i=0;i<n;++i) {
            int left = i==0?0:e[i-1];
            int right = i==n-1?eventTime:s[i+1];
            if(q[i]) ans = max(ans, right-left);
            else ans = max(ans, right-left-(e[i]-s[i]));
        }
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

func maxFreeTime(eventTime int, s []int, e []int) int {
    n := len(s)
    q := make([]bool, n)
    t1, t2 := 0, 0
    for i := 0; i < n; i++ {
        if e[i]-s[i] <= t1 {
            q[i] = true
        }
        if i == 0 {
            t1 = max(t1, s[i])
        } else {
            t1 = max(t1, s[i]-e[i-1])
        }
        if e[n-i-1]-s[n-i-1] <= t2 {
            q[n-i-1] = true
        }
        if i == 0 {
            t2 = max(t2, eventTime-e[n-1])
        } else {
            t2 = max(t2, s[n-i]-e[n-i-1])
        }
    }
    ans := 0
    for i := 0; i < n; i++ {
        left := 0
        if i > 0 {
            left = e[i-1]
        }
        right := eventTime
        if i < n-1 {
            right = s[i+1]
        }
        if q[i] {
            ans = max(ans, right-left)
        } else {
            ans = max(ans, right-left-(e[i]-s[i]))
        }
    }
    return ans
}
func max(a, b int) int { if a > b { return a } else { return b } }
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    public int maxFreeTime(int eventTime, int[] s, int[] e) {
        int n = s.length;
        boolean[] q = new boolean[n];
        for (int i = 0, t1 = 0, t2 = 0; i < n; i++) {
            if (e[i] - s[i] <= t1) q[i] = true;
            t1 = Math.max(t1, s[i] - (i == 0 ? 0 : e[i - 1]));
            if (e[n - i - 1] - s[n - i - 1] <= t2) q[n - i - 1] = true;
            t2 = Math.max(t2, (i == 0 ? eventTime : s[n - i]) - e[n - i - 1]);
        }
        int ans = 0;
        for (int i = 0; i < n; i++) {
            int left = i == 0 ? 0 : e[i - 1];
            int right = i == n - 1 ? eventTime : s[i + 1];
            if (q[i]) ans = Math.max(ans, right - left);
            else ans = Math.max(ans, right - left - (e[i] - s[i]));
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    fun maxFreeTime(eventTime: Int, s: IntArray, e: IntArray): Int {
        val n = s.size
        val q = BooleanArray(n)
        var t1 = 0; var t2 = 0
        for (i in 0 until n) {
            if (e[i] - s[i] <= t1) q[i] = true
            t1 = maxOf(t1, s[i] - if (i == 0) 0 else e[i-1])
            if (e[n-i-1] - s[n-i-1] <= t2) q[n-i-1] = true
            t2 = maxOf(t2, if (i == 0) eventTime else s[n-i] - e[n-i-1])
        }
        var ans = 0
        for (i in 0 until n) {
            val left = if (i == 0) 0 else e[i-1]
            val right = if (i == n-1) eventTime else s[i+1]
            if (q[i]) ans = maxOf(ans, right-left)
            else ans = maxOf(ans, right-left-(e[i]-s[i]))
        }
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def maxFreeTime(self, eventTime: int, s: list[int], e: list[int]) -> int:
        n = len(s)
        q = [False]*n
        t1 = t2 = 0
        for i in range(n):
            if e[i]-s[i] <= t1:
                q[i] = True
            t1 = max(t1, s[i] - (0 if i==0 else e[i-1]))
            if e[n-i-1]-s[n-i-1] <= t2:
                q[n-i-1] = True
            t2 = max(t2, (eventTime if i==0 else s[n-i]) - e[n-i-1])
        ans = 0
        for i in range(n):
            left = 0 if i==0 else e[i-1]
            right = eventTime if i==n-1 else s[i+1]
            if q[i]:
                ans = max(ans, right-left)
            else:
                ans = max(ans, right-left-(e[i]-s[i]))
        return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

impl Solution {
    pub fn max_free_time(event_time: i32, s: Vec<i32>, e: Vec<i32>) -> i32 {
        let n = s.len();
        let mut q = vec![false; n];
        let (mut t1, mut t2) = (0, 0);
        for i in 0..n {
            if e[i]-s[i] <= t1 { q[i]=true; }
            t1 = t1.max(s[i] - if i==0 {0} else {e[i-1]});
            if e[n-i-1]-s[n-i-1] <= t2 { q[n-i-1]=true; }
            t2 = t2.max(if i==0 {event_time} else {s[n-i]-e[n-i-1]});
        }
        let mut ans = 0;
        for i in 0..n {
            let left = if i==0 {0} else {e[i-1]};
            let right = if i==n-1 {event_time} else {s[i+1]};
            if q[i] { ans = ans.max(right-left); }
            else { ans = ans.max(right-left-(e[i]-s[i])); }
        }
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
    maxFreeTime(eventTime: number, s: number[], e: number[]): number {
        const n = s.length;
        const q: boolean[] = Array(n).fill(false);
        let t1 = 0, t2 = 0;
        for(let i=0;i<n;++i) {
            if(e[i]-s[i]<=t1) q[i]=true;
            t1 = Math.max(t1, s[i]-(i==0?0:e[i-1]));
            if(e[n-i-1]-s[n-i-1]<=t2) q[n-i-1]=true;
            t2 = Math.max(t2, (i==0?eventTime:s[n-i])-e[n-i-1]);
        }
        let ans = 0;
        for(let i=0;i<n;++i) {
            const left = i==0?0:e[i-1];
            const right = i==n-1?eventTime:s[i+1];
            if(q[i]) ans = Math.max(ans, right-left);
            else ans = Math.max(ans, right-left-(e[i]-s[i]));
        }
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n), since we only traverse the meetings a constant number of times.
  • 🧺 Space complexity: O(n), for the auxiliary array to track valid moves.