problemeasyalgorithmsleetcode-566leetcode 566leetcode566

Reshape the Matrix

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

In MATLAB, there is a handy function called reshape which can reshape an m x n matrix into a new one with a different size r x c keeping its original data.

You are given an m x n matrix mat and two integers r and c representing the number of rows and the number of columns of the wanted reshaped matrix.

The reshaped matrix should be filled with all the elements of the original matrix in the same row-traversing order as they were.

If the reshape operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.

Examples

Example 1


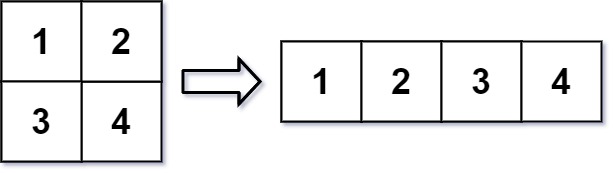
![](https://assets.leetcode.com/uploads/2021/04/24/reshape1-grid.jpg)

Input: mat = [[1,2],[3,4]], r = 1, c = 4
Output: [[1,2,3,4]]

Example 2


![](https://assets.leetcode.com/uploads/2021/04/24/reshape2-grid.jpg)

Input: mat = [[1,2],[3,4]], r = 2, c = 4
Output: [[1,2],[3,4]]

Constraints

  • m == mat.length
  • n == mat[i].length
  • 1 <= m, n <= 100
  • -1000 <= mat[i][j] <= 1000
  • 1 <= r, c <= 300

Solution

Method 1 - Flatten and Rebuild

Intuition

If the total number of elements matches, we can flatten the matrix and fill the new one row by row. Otherwise, return the original matrix.

Approach

Count the total elements. If mn != rc, return mat. Otherwise, flatten mat and fill the new matrix row by row.

Code

C++
#include <vector>
using namespace std;
class Solution {
public:
    vector<vector<int>> matrixReshape(vector<vector<int>>& mat, int r, int c) {
        int m = mat.size(), n = mat[0].size();
        if (m * n != r * c) return mat;
        vector<vector<int>> res(r, vector<int>(c));
        for (int i = 0; i < m * n; ++i)
            res[i / c][i % c] = mat[i / n][i % n];
        return res;
    }
};
Go
func matrixReshape(mat [][]int, r int, c int) [][]int {
    m, n := len(mat), len(mat[0])
    if m*n != r*c { return mat }
    res := make([][]int, r)
    for i := range res { res[i] = make([]int, c) }
    for i := 0; i < m*n; i++ {
        res[i/c][i%c] = mat[i/n][i%n]
    }
    return res
}
Java
class Solution {
    public int[][] matrixReshape(int[][] mat, int r, int c) {
        int m = mat.length, n = mat[0].length;
        if (m * n != r * c) return mat;
        int[][] res = new int[r][c];
        for (int i = 0; i < m * n; i++)
            res[i / c][i % c] = mat[i / n][i % n];
        return res;
    }
}
Kotlin
class Solution {
    fun matrixReshape(mat: Array<IntArray>, r: Int, c: Int): Array<IntArray> {
        val m = mat.size; val n = mat[0].size
        if (m * n != r * c) return mat
        val res = Array(r) { IntArray(c) }
        for (i in 0 until m * n)
            res[i / c][i % c] = mat[i / n][i % n]
        return res
    }
}
Python
class Solution:
    def matrixReshape(self, mat: list[list[int]], r: int, c: int) -> list[list[int]]:
        m, n = len(mat), len(mat[0])
        if m * n != r * c:
            return mat
        flat = [x for row in mat for x in row]
        return [flat[i*c:(i+1)*c] for i in range(r)]
Rust
impl Solution {
    pub fn matrix_reshape(mat: Vec<Vec<i32>>, r: i32, c: i32) -> Vec<Vec<i32>> {
        let m = mat.len();
        let n = mat[0].len();
        let (r, c) = (r as usize, c as usize);
        if m * n != r * c { return mat; }
        let mut res = vec![vec![0; c]; r];
        for i in 0..(m * n) {
            res[i / c][i % c] = mat[i / n][i % n];
        }
        res
    }
}
TypeScript
function matrixReshape(mat: number[][], r: number, c: number): number[][] {
    const m = mat.length, n = mat[0].length;
    if (m * n !== r * c) return mat;
    const flat = mat.flat();
    const res: number[][] = [];
    for (let i = 0; i < r; i++) res.push(flat.slice(i * c, (i + 1) * c));
    return res;
}

Complexity

  • ⏰ Time complexity: O(mn) — for flattening and filling the new matrix.
  • 🧺 Space complexity: O(mn) — for the new matrix.

Comments