Problem

Given a rectangular m * n two-dimensional matrix, write an algorithm to return all the diagonals of the matrix as a list of lists.

Examples:

Example 1:

1
2

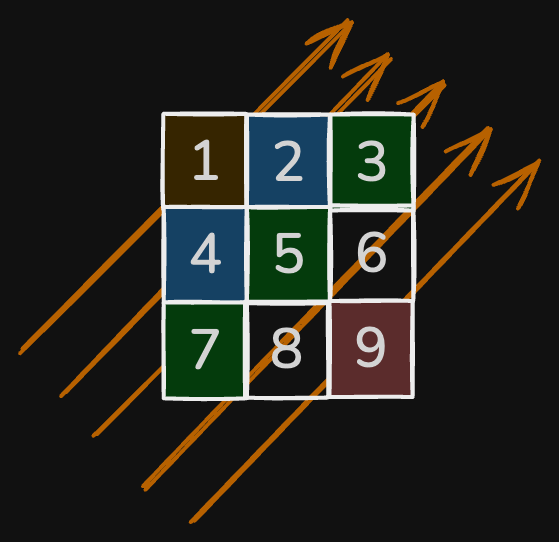
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]

Example 2:

$$ \begin {matrix} \colorbox{red}{1} & \colorbox{blue}{2} & \colorbox{green}{3} & \colorbox{magenta}{4} \\ \colorbox{blue}{5} & \colorbox{green}{6} & \colorbox{magenta}{7} & \colorbox{orange}{8} \\ \colorbox{green}{9} & \colorbox{magenta}{10} & \colorbox{orange}{11} & \colorbox{purple}{12} \\ \colorbox{magenta}{13} & \colorbox{orange}{14} & \colorbox{purple}{15} & \colorbox{grey}{16} \end {matrix} $$

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

Input: matrix = [
	[1, 2, 3, 4],
	[5, 6, 7, 8],
	[9, 10, 11, 12],
	[13, 14, 15, 16]
]
Output: [
	[1],
	[5, 2],
	[9, 6, 3],
	[13, 10, 7, 4],
	[14, 11, 8],
	[15, 12],
	[16]
]

Method 1 - Separating diagonals in first and second half

To extract all diagonals of a matrix, we can leverage the indexing properties of the matrix.

Here is the approach:

  1. Diagonal traversal:
    • We traverse from the bottom-left to the top-right for each diagonal in the matrix.
    • For each starting point, move upwards-right to gather elements of the diagonal.
  2. Handling Starting Points:
    • First, handle all starting points from the first column.
    • Next, handle all starting points from the top row (excluding the first element to avoid duplication).

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

public class Solution {
    public List<List<Integer>> getDiagonals(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        List<List<Integer>> result = new ArrayList<>();

        // Start from the first column
        for (int row = 0; row < m; row++) {
            List<Integer> diagonal = new ArrayList<>();
            int r = row, c = 0;
            while (r >= 0 && c < n) {
                diagonal.add(matrix[r][c]);
                r--;
                c++;
            }
            result.add(diagonal);
        }

        // Start from the top row (excluding the first element)
        for (int col = 1; col < n; col++) {
            List<Integer> diagonal = new ArrayList<>();
            int r = m - 1, c = col;
            while (r >= 0 && c < n) {
                diagonal.add(matrix[r][c]);
                r--;
                c++;
            }
            result.add(diagonal);
        }

        return result;
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        int[][] matrix = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12},
                {13, 14, 15, 16}
        };

        List<List<Integer>> diagonals = sol.getDiagonals(matrix);
        for (List<Integer> diag : diagonals) {
            System.out.println(diag);
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

class Solution:
    def get_diagonals(self, matrix):
        m, n = len(matrix), len(matrix[0])
        result = []

        # Start from the first column
        for row in range(m):
            diagonal = []
            r, c = row, 0
            while r >= 0 and c < n:
                diagonal.append(matrix[r][c])
                r -= 1
                c += 1
            result.append(diagonal)

        # Start from the top row (excluding the first element)
        for col in range(1, n):
            diagonal = []
            r, c = m - 1, col
            while r >= 0 and c < n:
                diagonal.append(matrix[r][c])
                r -= 1
                c += 1
            result.append(diagonal)

        return result

# Example usage
sol = Solution()
matrix = [
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16]
]

diagonals = sol.get_diagonals(matrix)
for diag in diagonals:
    print(diag)

Complexity

  • ⏰ Time complexity: O(m * n), where m is the number of rows and n is the number of columns. Each element in the matrix is visited exactly once.
  • 🧺 Space complexity: O(m * n) to store the results and the visited states.

Method 2 - Using Queue and BFS

Use a Breadth-First Search (BFS) with a queue to traverse each diagonal. Starting from each cell in the matrix, we enqueue the current cell and continue exploring its diagonal neighbours, until all of them are visited.

In order to understand the BFS approach for extracting diagonals from a matrix, let’s first observe the pattern. If you examine the zigzag or diagonal traversal, you’ll notice that moving either down or right from any element in one diagonal will lead you to elements of the consecutive diagonal. This insight is key to storing the upcoming diagonal elements in a queue while processing and collecting the current diagonal elements.

Here’s how the BFS solution works:

  1. Initialization: Start the process with the first element in the matrix at index (0, 0). Add this element to the queue for processing.
  2. Processing the Queue: While the queue is not empty, perform the following steps:
    1. Determine the current size of the queue. This size indicates the number of elements present at the current diagonal level.
    2. For each element in this diagonal level:
      • Dequeue the element from the front of the queue.
      • Collect this element as part of the current diagonal.
      • Add the elements that are positioned downward and rightward to the queue for future processing. (Edge cases are handled to ensure elements are not duplicated or out of matrix bounds).
    3. After processing all elements of the current diagonal, move on to the next level.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

public class Solution {
    public List<List<Integer>> getDiagonals(int[][] grid) {
        int m = grid.length;
        if (m == 0) {
            return new ArrayList<>();
        }
        int n = grid[0].length;
        List<List<Integer>> result = new ArrayList<>();

        Queue<Integer[]> queue = new LinkedList<>();

        // Process each diagonal starting from the first column
        for (int row = 0; row < m; row++) {
            queue.add(new Integer[]{row, 0});
            List<Integer> diagonal = new ArrayList<>();

            while (!queue.isEmpty()) {
                Integer[] position = queue.poll();
                int r = position[0];
                int c = position[1];

                if (r < m && c < n) {
                    diagonal.add(grid[r][c]);

                    if (r + 1 < m && c + 1 < n) {
                        queue.add(new Integer[]{r + 1, c + 1});
                    }
                }
            }
            result.add(diagonal);
        }

        // Process each diagonal starting from the top row (excluding the first element)
        for (int col = 1; col < n; col++) {
            queue.add(new Integer[]{m - 1, col});
            List<Integer> diagonal = new ArrayList<>();

            while (!queue.isEmpty()) {
                Integer[] position = queue.poll();
                int r = position[0];
                int c = position[1];

                if (r < m && c < n) {
                    diagonal.add(grid[r][c]);

                    if (r + 1 < m && c + 1 < n) {
                        queue.add(new Integer[]{r + 1, c + 1});
                    }
                }
            }
            result.add(diagonal);
        }

        return result;
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        int[][] matrix = {
                {1, 2, 3, 4},
                {5, 6, 7, 8},
                {9, 10, 11, 12},
                {13, 14, 15, 16}
        };

        List<List<Integer>> diagonals = sol.getDiagonals(matrix);
        for (List<Integer> diag : diagonals) {
            System.out.println(diag);
        }
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

class Solution:
    def get_diagonals(self, matrix):
        m = len(matrix)
        if m == 0:
            return []
        n = len(matrix[0])
        result = []

        queue = deque()

        # Process each diagonal starting from the first column
        for row in range(m):
            queue.append((row, 0))
            diagonal = []

            while queue:
                r, c = queue.popleft()
                if 0 <= r < m and 0 <= c < n:
                    diagonal.append(matrix[r][c])
                    if r + 1 < m and c + 1 < n:
                        queue.append((r + 1, c + 1))

            result.append(diagonal)

        # Process each diagonal starting from the top row (excluding the first element)
        for col in range(1, n):
            queue.append((m - 1, col))
            diagonal = []

            while queue:
                r, c = queue.popleft()
                if 0 <= r < m and 0 <= c < n:
                    diagonal.append(matrix[r][c])
                    if r + 1 < m and c + 1 < n:
                        queue.append((r + 1, c + 1))

            result.append(diagonal)

        return result

# Example usage
sol = Solution()
matrix = [
    [1, 2, 3, 4],
    [5, 6, 7, 8],
    [9, 10, 11, 12],
    [13, 14, 15, 16]
]

diagonals = sol.get_diagonals(matrix)
for diag in diagonals:
    print(diag)

Complexity

  • ⏰ Time complexity: O(m * n), where m is the number of rows and n is the number of columns.
  • 🧺 Space complexity: O(m * n) to store the results.