problemeasyalgorithmsleetcode-2103leetcode 2103leetcode2103

Rings and Rods

EasyUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There are n rings and each ring is either red, green, or blue. The rings are distributed across ten rods labeled from 0 to 9.

You are given a string rings of length 2n that describes the n rings that are placed onto the rods. Every two characters in rings forms a color-position pair that is used to describe each ring where:

  • The first character of the ith pair denotes the ith ring's color ('R', 'G', 'B').
  • The second character of the ith pair denotes the rod that the ith ring is placed on ('0' to '9').

For example, "R3G2B1" describes n == 3 rings: a red ring placed onto the rod labeled 3, a green ring placed onto the rod labeled 2, and a blue ring placed onto the rod labeled 1.

Return the number of rods that haveall three colors of rings on them.

Examples

Example 1


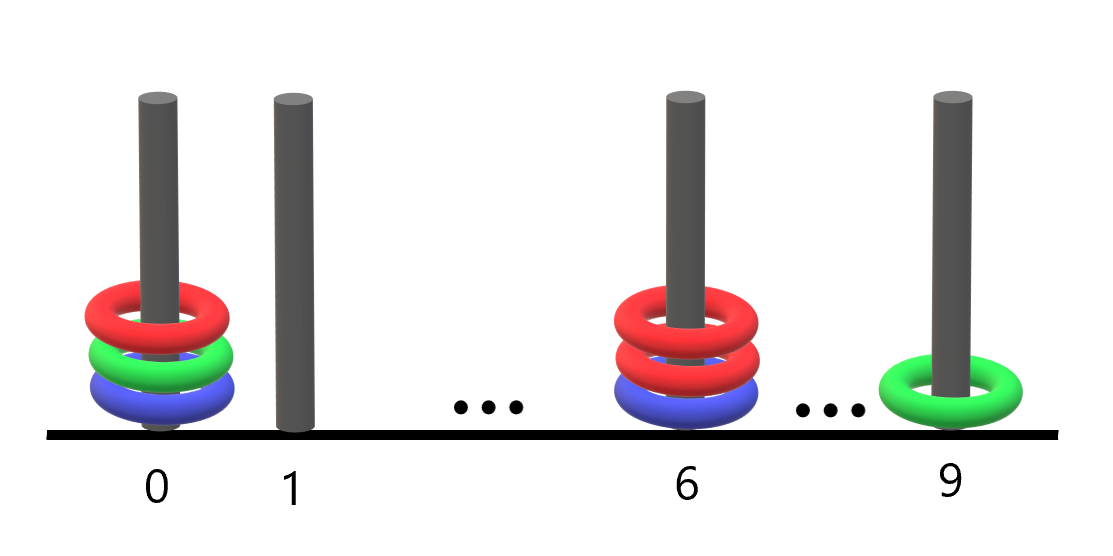
![](https://assets.leetcode.com/uploads/2021/11/23/ex1final.png)

Input: rings = "B0B6G0R6R0R6G9"
Output: 1
Explanation: 
- The rod labeled 0 holds 3 rings with all colors: red, green, and blue.
- The rod labeled 6 holds 3 rings, but it only has red and blue.
- The rod labeled 9 holds only a green ring.
Thus, the number of rods with all three colors is 1.

Example 2


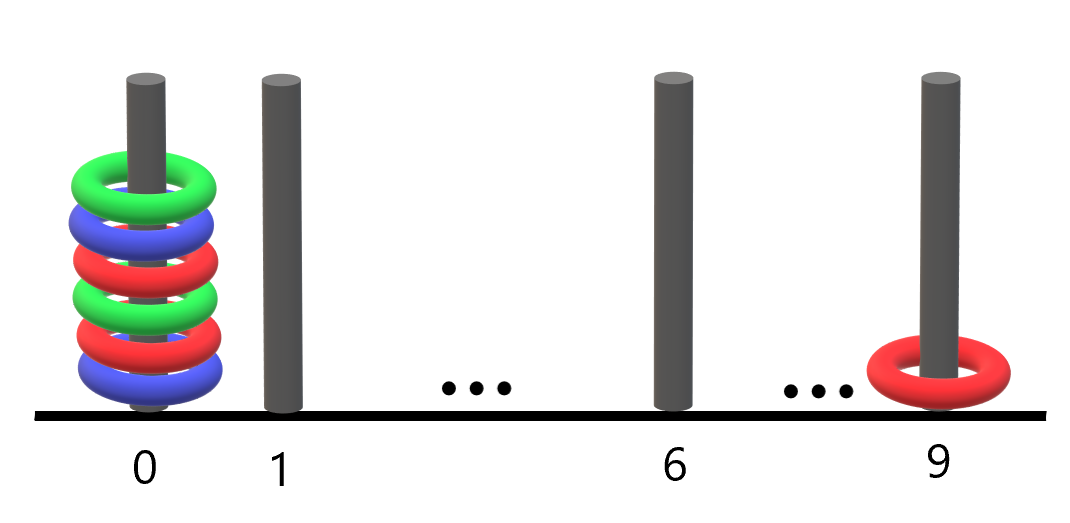
![](https://assets.leetcode.com/uploads/2021/11/23/ex2final.png)

Input: rings = "B0R0G0R9R0B0G0"
Output: 1
Explanation: 
- The rod labeled 0 holds 6 rings with all colors: red, green, and blue.
- The rod labeled 9 holds only a red ring.
Thus, the number of rods with all three colors is 1.

Example 3

Input: rings = "G4"
Output: 0
Explanation: 
Only one ring is given. Thus, no rods have all three colors.

Constraints

  • rings.length == 2 * n
  • 1 <= n <= 100
  • rings[i] where i is even is either 'R', 'G', or 'B' (0-indexed).
  • rings[i] where i is odd is a digit from '0' to '9' (0-indexed).

Solution

Method 1 - Hash Map by Rod

Intuition

We need to know, for each rod, which colors are present. If a rod has all three colors, it counts. This is a classic hash map (or array) problem.

Approach

Iterate through the string in steps of 2, mapping each rod to a set of colors. At the end, count how many rods have all three colors.

Code

C++
#include <unordered_set>
#include <vector>
using namespace std;
class Solution {
public:
    int countPoints(string rings) {
        vector<unordered_set<char>> rods(10);
        for (int i = 0; i < rings.size(); i += 2) {
            char color = rings[i];
            int rod = rings[i+1] - '0';
            rods[rod].insert(color);
        }
        int res = 0;
        for (auto& s : rods) if (s.size() == 3) res++;
        return res;
    }
};
Go
func countPoints(rings string) int {
    rods := make([]map[byte]bool, 10)
    for i := range rods { rods[i] = make(map[byte]bool) }
    for i := 0; i < len(rings); i += 2 {
        color := rings[i]
        rod := rings[i+1] - '0'
        rods[rod][color] = true
    }
    res := 0
    for _, s := range rods {
        if len(s) == 3 { res++ }
    }
    return res
}
Java
import java.util.*;
class Solution {
    public int countPoints(String rings) {
        Set<Character>[] rods = new HashSet[10];
        for (int i = 0; i < 10; i++) rods[i] = new HashSet<>();
        for (int i = 0; i < rings.length(); i += 2) {
            char color = rings.charAt(i);
            int rod = rings.charAt(i+1) - '0';
            rods[rod].add(color);
        }
        int res = 0;
        for (Set<Character> s : rods) if (s.size() == 3) res++;
        return res;
    }
}
Kotlin
class Solution {
    fun countPoints(rings: String): Int {
        val rods = Array(10) { mutableSetOf<Char>() }
        for (i in rings.indices step 2) {
            val color = rings[i]
            val rod = rings[i+1].digitToInt()
            rods[rod].add(color)
        }
        return rods.count { it.size == 3 }
    }
}
Python
class Solution:
    def countPoints(self, rings: str) -> int:
        rods = [set() for _ in range(10)]
        for i in range(0, len(rings), 2):
            color = rings[i]
            rod = int(rings[i+1])
            rods[rod].add(color)
        return sum(1 for s in rods if len(s) == 3)
Rust
impl Solution {
    pub fn count_points(rings: String) -> i32 {
        let mut rods = vec![std::collections::HashSet::new(); 10];
        let bytes = rings.as_bytes();
        let n = bytes.len();
        let mut i = 0;
        while i < n {
            let color = bytes[i] as char;
            let rod = (bytes[i+1] - b'0') as usize;
            rods[rod].insert(color);
            i += 2;
        }
        rods.iter().filter(|s| s.len() == 3).count() as i32
    }
}
TypeScript
function countPoints(rings: string): number {
    const rods: Set<string>[] = Array.from({length: 10}, () => new Set());
    for (let i = 0; i < rings.length; i += 2) {
        const color = rings[i];
        const rod = Number(rings[i+1]);
        rods[rod].add(color);
    }
    return rods.filter(s => s.size === 3).length;
}

Complexity

  • ⏰ Time complexity: O(n) — where n is the length of rings.
  • 🧺 Space complexity: O(1) — at most 10 rods, each with up to 3 colors.

Comments