Rotate n x n matrix by 90 degrees

Problem

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise). You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Another way to ask the same problem

Given an image represented by an NxN matrix, where each pixel in the image is 4 bytes, write a method to rotate the image by 90 degrees. Can you do this in place?

Examples

Example 1:

Input: matrix =[[1,2,3],[4,5,6],[7,8,9]]
Output:[[7,4,1],[8,5,2],[9,6,3]]

Example 2:

Input: matrix =[[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Solution

Consider the matrix from example 2 follow the dry run.

Video explanation

Here is the video explaining below methods in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/xB1cnwlvQSk" frameborder="0" allowfullscreen></iframe></div>

Method 1 - Naive approach using a copy matrix

Intuition

The simplest way to understand matrix rotation is to think of the movement of elements in columns to rows. For a rotated matrix:

• The first row of the original matrix becomes the last column in the rotated version.
• The second row becomes the second-last column, and so on.

This can be achieved easily by creating a copy matrix to store the rotated version. Then, copy this rotated matrix back into the original matrix to satisfy the "in-place" requirement.

Approach

1. Create a new matrix to store the rotated version.
2. Use two nested loops to map the positions of each element:
   • The element at matrix[i][j] moves to the position rotated[j][n - 1 - i].
3. Copy the rotated matrix back to the original matrix.

Code

Java

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        int[][] rotated = new int[n][n];
        
        // Step 1: Create temporary rotated copy
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                rotated[j][n - 1 - i] = matrix[i][j];
            }
        }
        
        // Step 2: Copy back to original matrix
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                matrix[i][j] = rotated[i][j];
            }
        }
    }
}

Python

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # Step 1: Create a temporary rotated version
        rotated: List[List[int]] = [[0] * n for _ in range(n)]
        for i in range(n):
            for j in range(n):
                # Compute rotated position
                rotated[j][n-1-i] = matrix[i][j]
        
        # Step 2: Copy rotated version back into the original matrix
        for i in range(n):
            for j in range(n):
                matrix[i][j] = rotated[i][j]

Dry Run

Lets understand this by example. Consider the array :

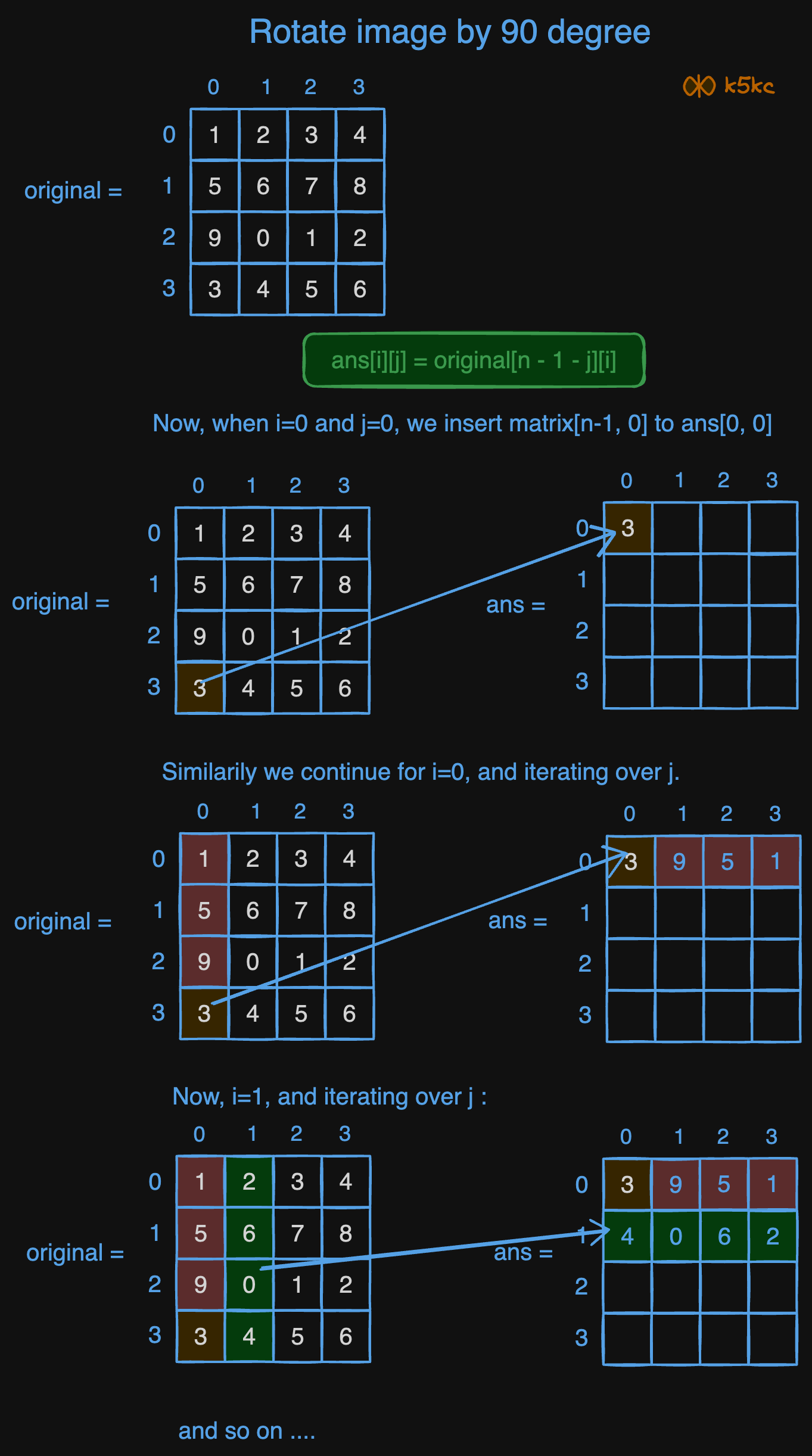
Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(n^2)

But as we are using lots of space, can we do better?

Method 2 - Four swap technique - layered looping

Intuition

Matrix rotation can also be viewed as a layer-by-layer process:

• Each layer of the matrix resembles a square ring.
• Elements move clockwise within the ring:
  • Top → Right → Bottom → Left → Top.
• By performing these swaps one element at a time, the rotation is achieved without extra space.

Approach

1. Identify concentric layers in the matrix (e.g., outermost layer, 2nd layer, etc.).
2. For each layer:
   • Iterate over the top row of the layer (i indexes the columns).
   • For each element in the top row:
     • Perform four swaps:
       • Top element → Right column.
       • Right column → Bottom row.
       • Bottom row → Left column.
       • Left column → Top row.
3. Repeat for all layers until the entire matrix is rotated.

Code

Java

class Solution {
    public void rotate(int[][] matrix) {
        int n = matrix.length;
        // Process each layer
        for (int layer = 0; layer < n / 2; layer++) {
            for (int i = layer; i < n - layer - 1; i++) { // For each element in the layer
                // Save the top element
                int top = matrix[layer][i];
                
                // Perform the four swaps
                // Left -> Top
                matrix[layer][i] = matrix[n - i - 1][layer];
                
                // Bottom -> Left
                matrix[n - i - 1][layer] = matrix[n - layer - 1][n - i - 1];
                
                // Right -> Bottom
                matrix[n - layer - 1][n - i - 1] = matrix[i][n - layer - 1];
                
                // Top -> Right
                matrix[i][n - layer - 1] = top;
            }
        }
    }
}

Python

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        n = len(matrix)
        # Process each layer
        for layer in range(n // 2):     
            for i in range(layer, n - layer - 1): # For each element in the layer
                # Save the top element
                top = matrix[layer][i]
                
                # Perform the four swaps
                # Left -> Top
                matrix[layer][i] = matrix[n - i - 1][layer]
                
                # Bottom -> Left
                matrix[n - i - 1][layer] = matrix[n - layer - 1][n - i - 1]
                
                # Right -> Bottom
                matrix[n - layer - 1][n - i - 1] = matrix[i][n - layer - 1]
                
                # Top -> Right
                matrix[i][n - layer - 1] = top

Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(1)

Method 3 - Four swap technique - different looping

This example is taken from here. Here is the basic algo:

1. Iterate over the 2D array with i and j iterators to the size of N/2
2. Now take the corner elements based on i and j, and swap them accordingly

This method is similar to method 1, we were doing this in method 1:

ret[i, j] = matrix[n - j - 1, i];

that means we have to save matrix[i][j] to to temp variable, before updating it with matrix[n-1-j][i]

Code

Java

class Solution {

	public static void rotate(int[][] matrix) {
		int n = matrix.length; // Renamed N to n for clarity
		for (int i = 0; i < n / 2; ++i) {
			for (int j = 0; j<(n + 1) / 2; ++j) {
				int temp = matrix[i][j]; // save the top element;
				matrix[i][j] = matrix[n - 1 - j][i]; // right -> top;
				matrix[n - 1 - j][i] = matrix[n - 1 - i][n - 1 - j]; // bottom -> right;
				matrix[n - 1 - i][n - 1 - j] = matrix[j][n - 1 - i]; // left -> bottom;
				matrix[j][n - 1 - i] = temp; // top -> left;
			}
		}
	}

}

Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(1)

Dry Run

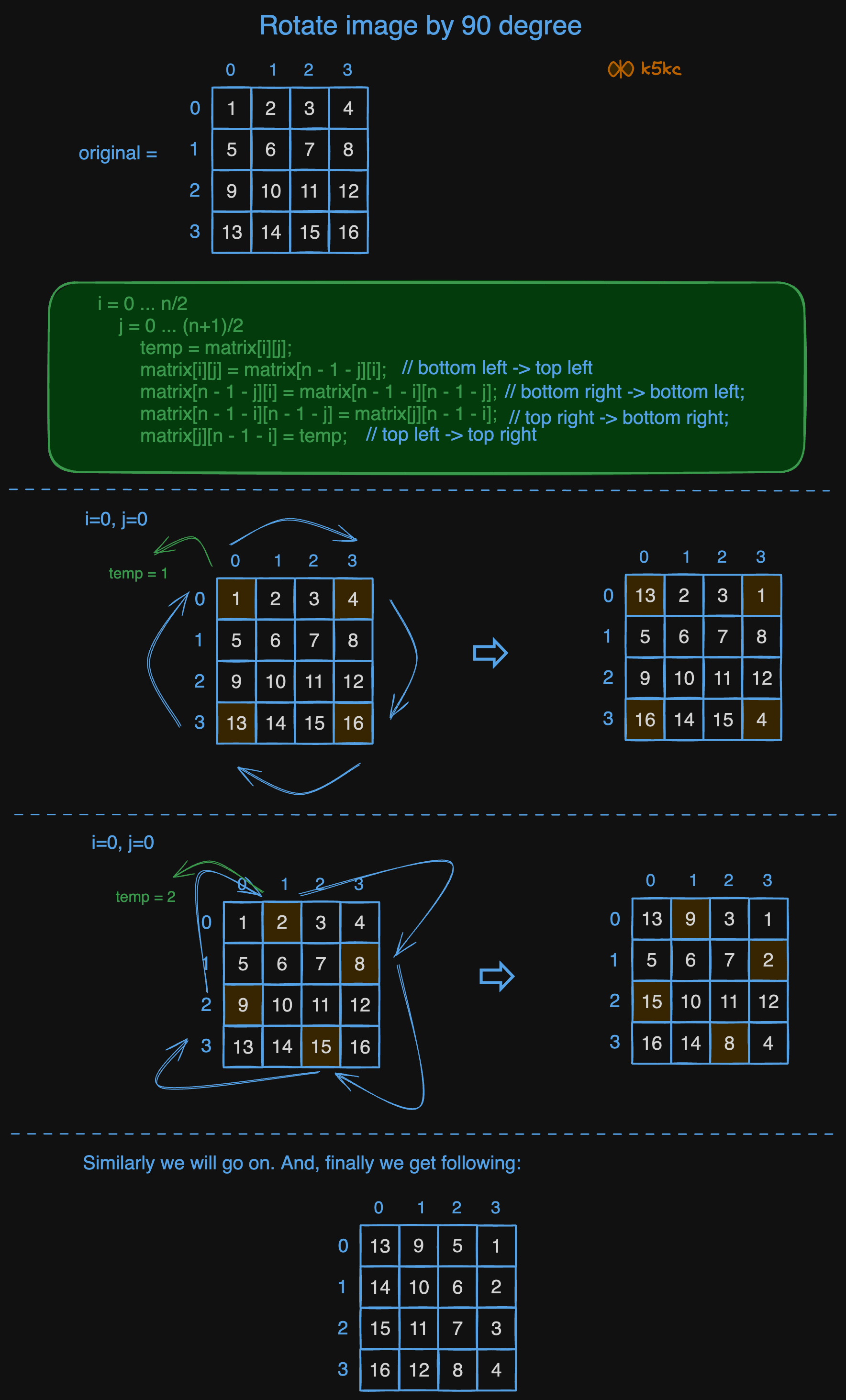
So, to sum up we were doing this:

1 4

13 16

then we rotate the following diamond which is sort of askew

   2
           8
9      
       15

and then the 2nd skewed diamond

       3
5          
           12
   14

so that takes care of the outer edge so essentially we do that one shell at a time until finally the middle square (or if it's odd just the final element which does not move)

6 7
10 11

so now let's figure out the indices of each layer, assume we always work with the outermost layer, we are doing

[0,0] -> [0,n-1], [0,n-1] -> [n-1,n-1], [n-1,n-1] -> [n-1,0], and [n-1,0] -> [0,0]
[0,1] -> [1,n-1], [1,n-2] -> [n-1,n-2], [n-1,n-2] -> [n-2,0], and [n-2,0] -> [0,1]
[0,2] -> [2,n-2], [2,n-2] -> [n-1,n-3], [n-1,n-3] -> [n-3,0], and [n-3,0] -> [0,2]

so on and so onuntil we are halfway through the edge so in general the pattern is

[0,i] -> [i,n-i], [i,n-i] -> [n-1,n-(i+1)], [n-1,n-(i+1)] -> [n-(i+1),0], and [n-(i+1),0] to [0,i]

Can we do better. It may not look obvious, but yes we can. Here is the next solution:

Method 4 - Using Transpose and Reverse

Intuition

Rotating a matrix is equivalent to transposing it (converting rows into columns) followed by reversing each row:

• Transpose rearranges the matrix by swapping matrix[i][j] with matrix[j][i], making rows into columns. (You can read more here: [Transpose of a Matrix](transpose-of-a-matrix).)
• Reversing rows aligns the columns into their proper clockwise-rotated order.

This method is both intuitive and simple, breaking the problem into two manageable steps.

Approach

1. Transpose the matrix:
   • Swap elements above the diagonal (matrix[i][j] ↔ matrix[j][i] where j > i).
2. Reverse each row:
   • For each row, reverse its elements in place (swap elements symmetrically from start to end).

Here is how it will work (as gif):

Or if you prefer to watch silent video: <div class="youtube-embed"><iframe src="https://www.youtube.com/embed/laYqkeZsg9Q" frameborder="0" allowfullscreen></iframe></div>

Code

Java

public class Solution {
    public void rotate(int[][] matrix) {
        // Step 1: Transpose the matrix
        transpose(matrix);

        // Step 2: Reverse each row
        reverseRows(matrix);
    }

    private void transpose(int[][] matrix) {
        int n = matrix.length;

        // Swap elements above the diagonal
        for (int i = 0; i < n; i++) {
            for (int j = i + 1; j < n; j++) {  // Start at j = i + 1 to avoid swapping diagonal
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
    }

    private void reverseRows(int[][] matrix) {
        int n = matrix.length;

        // Iterate through rows
        for (int i = 0; i < n; i++) {
            // Loop to the middle of the row
            for (int j = 0; j < n / 2; j++) {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[i][n - j - 1];
                matrix[i][n - j - 1] = temp;
            }
        }
    }
}

Python

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        # Step 1: Transpose the matrix
        self.transpose(matrix)

        # Step 2: Reverse each row
        self.reverseRows(matrix)

    def transpose(self, matrix: List[List[int]]) -> None:
        n = len(matrix)

        # Swap elements above the diagonal
        for i in range(n):
            for j in range(i + 1, n):  # Start at j = i + 1 to avoid swapping diagonal
                matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]

    def reverseRows(self, matrix: List[List[int]]) -> None:
        n = len(matrix)

        # Iterate through rows
        for i in range(n):
            # Loop to the middle of the row
            for j in range(n // 2):
                temp = matrix[i][j]
                matrix[i][j] = matrix[i][n - j - 1]
                matrix[i][n - j - 1] = temp

Complexity

• ⏰ Time complexity: O(n^2)
• 🧺 Space complexity: O(1)

Method 5 - Adding Decorator on the Top of Matrix

This method has been suggested by Drew here. Just keeping it here: Whilst rotating the data in place might be necessary (perhaps to update the physically stored representation), it becomes simpler and possibly more performant to add a layer of indirection onto the array access, perhaps an interface:

interface IReadableMatrix {
 int GetValue(int x, int y);
}

If your Matrix already implements this interface, then it can be rotated via a decorator class like this:

class RotatedMatrix: IReadableMatrix {
    private readonly IReadableMatrix _baseMatrix;

    public RotatedMatrix(IReadableMatrix baseMatrix) {
        _baseMatrix = baseMatrix;
    }

    int GetValue(int x, int y) {
        // transpose x and y dimensions
        return _baseMatrix(y, x);
    }
}

Rotating +90/-90/180 degrees, flipping horizontally/vertically and scaling can all be achieved in this fashion as well. Performance would need to be measured in your specific scenario. However the O(n^2) operation has now been replaced with an O(1) call. It's a virtual method call which is slower than direct array access, so it depends upon how frequently the rotated array is used after rotation. If it's used once, then this approach would definitely win. If it's rotated then used in a long-running system for days, then in-place rotation might perform better. It also depends whether you can accept the up-front cost. As with all performance issues, measure, measure, measure!