Same Tree

Problem

Given the roots of two binary trees p and q, write a function to check if they are the same or not.

Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.

For e.g. in the below diagram, example 1 has identical trees but example 2 doesnt.

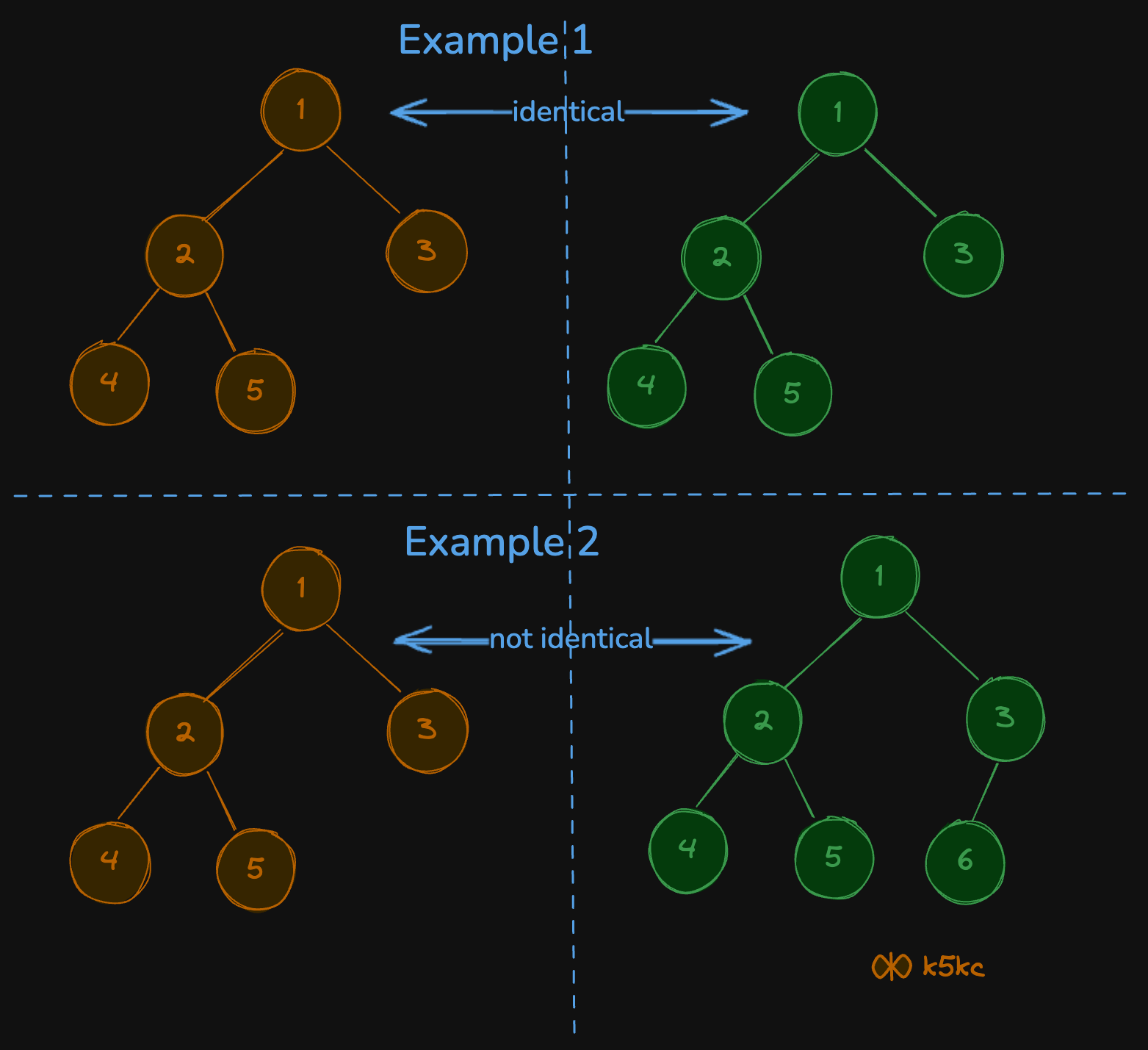
Examples

Example 1

flowchart LR
    subgraph p ["Tree p"]
        A(1):::orange
        B(2):::orange
        C(3):::orange
        A --- B & C
    end
    subgraph q ["Tree q"]
        D(1):::green
        E(2):::green
        F(3):::green
        D --- E & F
    end
    p <==>|Identical| q

    classDef green fill:#3CB371,stroke:#000,stroke-width:1px,color:#fff; 
classDef blue fill:#0000FF,stroke:#000,stroke-width:1px,color:#fff;
classDef orange fill:#DC582A,stroke:#333,stroke-width:2px;

linkStyle 4 stroke:blue,stroke-width:2px

Input: p = [1,2,3], q = [1,2,3]
Output: true

Example 2

flowchart LR
    subgraph p ["Tree p"]
        A(1)
        B(2)
        A --- B
        A ~~~ N1:::hidden
    end
    subgraph q ["Tree q"]
        D(1)
        E(2)
        D ~~~ N2:::hidden
        D --- E
    end
    
    
    p <==>|Not Identical| q
    classDef hidden display:none

Input: p = [1,2], q = [1,null,2]
Output: false

Example 3

flowchart LR
    subgraph p ["Tree p"]
        A(1)
        B(2)
        C(1)
        A --- B
        A --- C
    end
    subgraph q ["Tree q"]
        D(1)
        E(1)
        F(2)
        D --- E
        D --- F
    end
    p <==>|Not Identical| q

Input: p = [1,2,1], q = [1,1,2]
Output: false

Solution

Method 1 - Recursive

Algorithm

• Recursive Traversal: Begin by traversing both trees simultaneously from their roots.
• Match Check: If either root is null or their data doesn't match, return false (structural or value mismatch).
• Subtree Verification: Recursively check if p.left is a subtree of q.left and p.right is a subtree of q.right.
• Completion Consistency: If one tree finishes traversing (null) while the other has nodes, return false (structural difference).
• Match Confirmation: If both trees reach the end simultaneously (both null), return true (trees match).

Video explanation

Here is the video explaining this method in detail. Please check it out:

<div class="youtube-embed"><iframe src="https://www.youtube.com/embed/Cq1LF5WJWY8" frameborder="0" allowfullscreen></iframe></div>

Complexity

• ⏰ Time complexity: O(n) — Each node in both trees is visited exactly once.
• 🧺 Space complexity: O(h) — The maximum depth of the recursion stack is the height of the tree (h). In the worst case (skewed tree), this is O(n); for a balanced tree, it is O(log n).

Code

Java

public boolean isSameTree(TreeNode p, TreeNode q) {
    if (p == null && q == null) {
        return true;
    }
    if (p == null || q == null) {
        return false;
    }

    return p.val == q.val &&
        isSameTree(p.left, q.left) &&
        isSameTree(p.right, q.right);
}

Python

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        # If both nodes are null, they are identical.
        if not p and not q:
            return True
        # If one is null or their values are different, they are not identical.
        if not p or not q or p.val != q.val:
            return False
        # Recursively check the left and right subtrees.
        return self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)

Rust

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn is_same_tree(p: Option<Rc<RefCell<TreeNode>>>, q: Option<Rc<RefCell<TreeNode>>>) -> bool {
        match (p, q) {
            (None, None) => true,
            (Some(p), Some(q)) => {
                let p = p.borrow();
                let q = q.borrow();
                p.val == q.val
                    && Self::is_same_tree(p.left.clone(), q.left.clone())
                    && Self::is_same_tree(p.right.clone(), q.right.clone())
            }
            _ => false,
        }
    }
}

Details on Rust code

A regular rust user would see this line

#[derive(Debug, PartialEq, Eq)]
pub struct TreeNode {

and deduce that Eq is already derived for TreeNode and hence the equivalence of TreeNode can just as simple as p == q

pub fn is_same_tree(p: Option<Rc<RefCell<TreeNode>>>, q: Option<Rc<RefCell<TreeNode>>>) -> bool {
    p == q
}

Method 2 - Iterative using Level Order Traversal

Intuition

Instead of recursion, we can use queues to traverse both trees in parallel, level by level. By comparing nodes at each level, we can efficiently check for structural and value equality without relying on the call stack.

Approach

1. Initialize two queues, one for each tree, and enqueue their roots.
2. While both queues are not empty:
   • Dequeue a node from each queue.
   • If both nodes are null, continue (they match at this position).
   • If only one is null or their values differ, return false (trees differ).
   • Enqueue the left and right children of both nodes for further comparison.
3. After traversal, if both queues are empty, the trees are identical; otherwise, they differ.

Complexity

• ⏰ Time complexity: O(n) — Each node in both trees is enqueued and dequeued exactly once.
• 🧺 Space complexity: O(w) — The maximum number of nodes in the queue at any time is the width of the tree (w). In the worst case (complete binary tree), this is O(n); for a skewed tree, it is O(1).

Code

C++

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        std::queue<TreeNode*> queue1, queue2;
        queue1.push(p);
        queue2.push(q);
        while (!queue1.empty() && !queue2.empty()) {
            TreeNode* node1 = queue1.front(); queue1.pop();
            TreeNode* node2 = queue2.front(); queue2.pop();
            if (!node1 && !node2) continue;
            if (!node1 || !node2 || node1->val != node2->val) return false;
            queue1.push(node1->left);
            queue1.push(node1->right);
            queue2.push(node2->left);
            queue2.push(node2->right);
        }
        return queue1.empty() && queue2.empty();
    }
};

Go

func isSameTree(p *TreeNode, q *TreeNode) bool {
    type Pair struct {
        p, q *TreeNode
    }
    var queue []Pair
    queue = append(traverse, Pair{p, q})
    for len(traverse) > 0 {
        pair := queue[len(traverse) - 1]
        traverse = queue[:len(traverse) - 1]
        if pair.p != nil && pair.q != nil && pair.p.Val == pair.q.Val {
            traverse = append(traverse, Pair{pair.p.Left, pair.q.Left})
            traverse = append(traverse, Pair{pair.p.Right, pair.q.Right})
        } else if pair.p != nil || pair.q != nil {
            return false
        }
    }
    return true
}

Java

class Solution {
	public boolean isSameTree(TreeNode p, TreeNode q) {
		Queue<TreeNode> queue1 = new LinkedList<>();
		Queue<TreeNode> queue2 = new LinkedList<>();
	
		queue1.offer(p);
		queue2.offer(q);
	
		while (!queue1.isEmpty() && !queue2.isEmpty()) {
			TreeNode node1 = queue1.poll();
			TreeNode node2 = queue2.poll();
	
			if (node1 == null && node2 == null) {
				continue;
			}
			if (node1 == null || node2 == null || node1.val != node2.val) {
				return false;
			}
	
			queue1.offer(node1.left);
			queue1.offer(node1.right);
			queue2.offer(node2.left);
			queue2.offer(node2.right);
		}
	
		return queue1.isEmpty() && queue2.isEmpty();
	}
}

Python

class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        queue1, queue2 = deque([p]), deque([q])
        while queue1 and queue2:
            node1, node2 = queue1.popleft(), queue2.popleft()
            if not node1 and not node2:
                continue
            if not node1 or not node2 or node1.val != node2.val:
                return False
            queue1.append(node1.left)
            queue1.append(node1.right)
            queue2.append(node2.left)
            queue2.append(node2.right)
        return not queue1 and not queue2

Rust

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn is_same_tree(p: Option<Rc<RefCell<TreeNode>>>, q: Option<Rc<RefCell<TreeNode>>>) -> bool {
        let mut queue = Vec::new();
        queue.push((p, q));
        while let Some((mut p, mut q)) = queue.pop() {
            if p.is_none() != q.is_none() {
                return false
            } else if let (Some(p), Some(q)) = (p.take(), q.take()) {
                let (mut p, mut q) = (p.borrow_mut(), q.borrow_mut());
                if p.val != q.val {
                    return false
                }
                queue.push((p.left.take(), q.left.take()));
                queue.push((p.right.take(), q.right.take()));
            }
        }
        true
    }
}

Method 3 - Iterative using DFS

Intuition

Instead of using recursion or queues, we can use stacks to traverse both trees in parallel, simulating a depth-first traversal. By comparing nodes as we pop them from the stack, we can check for both structural and value equality. This approach avoids recursion and leverages explicit stack management for control over traversal order.

Approach

1. Initialize two stacks, one for each tree, and push their roots.
2. While both stacks are not empty:
   • Pop a node from each stack.
   • If both nodes are null, continue (they match at this position).
   • If only one is null or their values differ, return false (trees differ).
   • Push the left and right children of both nodes onto their respective stacks for further comparison.
3. After traversal, if both stacks are empty, the trees are identical; otherwise, they differ.

Complexity

• ⏰ Time complexity: O(n) — Each node in both trees is pushed and popped from the stack exactly once.
• 🧺 Space complexity: O(h) — The maximum number of nodes in the stack at any time is the height of the tree (h). In the worst case (skewed tree), this is O(n); for a balanced tree, it is O(log n).

Code

Java

public boolean isSameTree(TreeNode p, TreeNode q) {
	Stack<TreeNode> stack1 = new Stack<>();
	Stack<TreeNode> stack2 = new Stack<>();

	stack1.push(p);
	stack2.push(q);

	while (!stack1.isEmpty() && !stack2.isEmpty()) {
		TreeNode node1 = stack1.pop();
		TreeNode node2 = stack2.pop();

		if (node1 == null && node2 == null) {
			continue;
		} else if (node1 == null || node2 == null || node1.val != node2.val) {
			return false;
		}

		stack1.push(node1.left);
		stack2.push(node2.left);

		stack1.push(node1.right);
		stack2.push(node2.right);
	}

	return stack1.isEmpty() && stack2.isEmpty();
}

Python

from typing import Optional
class Solution:
    def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
        stack1, stack2 = [p], [q]
        while stack1 and stack2:
            node1, node2 = stack1.pop(), stack2.pop()
            if not node1 and not node2:
                continue
            if not node1 or not node2 or node1.val != node2.val:
                return False
            stack1.append(node1.left)
            stack2.append(node2.left)
            stack1.append(node1.right)
            stack2.append(node2.right)
        return not stack1 and not stack2