Problem

Given a non-empty special binary tree consisting of nodes with the non-negative value, where each node in this tree has exactly two or zero sub-node. If the node has two sub-nodes, then this node’s value is the smaller value among its two sub-nodes. More formally, the property root.val = min(root.left.val, root.right.val) always holds.

Given such a binary tree, you need to output the second minimum value in the set made of all the nodes’ value in the whole tree.

If no such second minimum value exists, output -1 instead.

Examples

Example 1

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2020/10/15/smbt1.jpg)

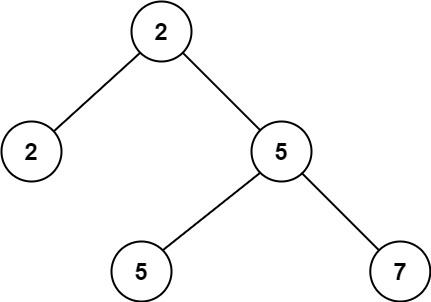
Input: root = [2,2,5,null,null,5,7]
Output: 5
Explanation: The smallest value is 2, the second smallest value is 5.

Example 2

1
2
3
4
5
6


![](https://assets.leetcode.com/uploads/2020/10/15/smbt2.jpg)

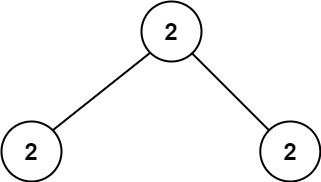
Input: root = [2,2,2]
Output: -1
Explanation: The smallest value is 2, but there isn't any second smallest value.

Constraints

  • The number of nodes in the tree is in the range [1, 25].
  • 1 <= Node.val <= 2^31 - 1
  • root.val == min(root.left.val, root.right.val) for each internal node of the tree.

Solution

Method 1 - DFS for Second Minimum

Intuition

The root is always the minimum value. The second minimum must be the smallest value in the tree that is greater than the root. We can traverse the tree and track the smallest value greater than root.val.

Approach

  1. Store the root value as min1.
  2. Traverse the tree (DFS or BFS). For each node:
    • If node.val > min1, update the answer if it’s smaller than current answer.
    • If node.val == min1, keep searching its children.
  3. Return the answer if found, else -1.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

struct TreeNode {
    int val;
    TreeNode *left, *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
    int findSecondMinimumValue(TreeNode* root) {
        int min1 = root->val, ans = -1;
        function<void(TreeNode*)> dfs = [&](TreeNode* node) {
            if (!node) return;
            if (node->val > min1) {
                if (ans == -1 || node->val < ans) ans = node->val;
            } else if (node->val == min1) {
                dfs(node->left); dfs(node->right);
            }
        };
        dfs(root);
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

type TreeNode struct {
    Val int
    Left, Right *TreeNode
}
func findSecondMinimumValue(root *TreeNode) int {
    min1, ans := root.Val, -1
    var dfs func(*TreeNode)
    dfs = func(node *TreeNode) {
        if node == nil { return }
        if node.Val > min1 {
            if ans == -1 || node.Val < ans { ans = node.Val }
        } else if node.Val == min1 {
            dfs(node.Left); dfs(node.Right)
        }
    }
    dfs(root)
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

class TreeNode {
    int val;
    TreeNode left, right;
    TreeNode(int x) { val = x; }
}
class Solution {
    public int findSecondMinimumValue(TreeNode root) {
        int min1 = root.val, ans = -1;
        ans = dfs(root, min1, ans);
        return ans;
    }
    private int dfs(TreeNode node, int min1, int ans) {
        if (node == null) return ans;
        if (node.val > min1) {
            if (ans == -1 || node.val < ans) ans = node.val;
        } else if (node.val == min1) {
            ans = dfs(node.left, min1, ans);
            ans = dfs(node.right, min1, ans);
        }
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class TreeNode(var `val`: Int) {
    var left: TreeNode? = null
    var right: TreeNode? = null
}
class Solution {
    fun findSecondMinimumValue(root: TreeNode?): Int {
        val min1 = root!!.`val`
        var ans = -1
        fun dfs(node: TreeNode?) {
            if (node == null) return
            if (node.`val` > min1) {
                if (ans == -1 || node.`val` < ans) ans = node.`val`
            } else if (node.`val` == min1) {
                dfs(node.left); dfs(node.right)
            }
        }
        dfs(root)
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
def findSecondMinimumValue(root):
    min1 = root.val
    ans = -1
    def dfs(node):
        nonlocal ans
        if not node:
            return
        if node.val > min1:
            if ans == -1 or node.val < ans:
                ans = node.val
        elif node.val == min1:
            dfs(node.left)
            dfs(node.right)
    dfs(root)
    return ans
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

use std::rc::Rc;
use std::cell::RefCell;
// Definition for a binary tree node.
// struct TreeNode { val: i32, left: Option<Rc<RefCell<TreeNode>>>, right: Option<Rc<RefCell<TreeNode>>> }
pub fn find_second_minimum_value(root: Option<Rc<RefCell<TreeNode>>>) -> i32 {
    let min1 = root.as_ref().unwrap().borrow().val;
    let mut ans = -1;
    fn dfs(node: &Option<Rc<RefCell<TreeNode>>>, min1: i32, ans: &mut i32) {
        if let Some(n) = node {
            let v = n.borrow().val;
            if v > min1 {
                if *ans == -1 || v < *ans { *ans = v; }
            } else if v == min1 {
                dfs(&n.borrow().left, min1, ans);
                dfs(&n.borrow().right, min1, ans);
            }
        }
    }
    dfs(&root, min1, &mut ans);
    ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class TreeNode {
    val: number
    left: TreeNode | null
    right: TreeNode | null
    constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
        this.val = (val===undefined ? 0 : val)
        this.left = (left===undefined ? null : left)
        this.right = (right===undefined ? null : right)
    }
}
function findSecondMinimumValue(root: TreeNode | null): number {
    const min1 = root!.val
    let ans = -1
    function dfs(node: TreeNode | null) {
        if (!node) return
        if (node.val > min1) {
            if (ans === -1 || node.val < ans) ans = node.val
        } else if (node.val === min1) {
            dfs(node.left); dfs(node.right)
        }
    }
    dfs(root)
    return ans
}

Complexity

  • ⏰ Time complexity: O(n) (visit each node once)
  • 🧺 Space complexity: O(h) (recursion stack, h = tree height)