Select Cells in Grid With Maximum Score
HardUpdated: Aug 2, 2025
Practice on:
Problem
You are given a 2D matrix grid consisting of positive integers.
You have to select one or more cells from the matrix such that the following conditions are satisfied:
- No two selected cells are in the same row of the matrix.
- The values in the set of selected cells are unique.
Your score will be the sum of the values of the selected cells.
Return the maximum score you can achieve.
Examples
Example 1
Input: grid = [[1,2,3],[4,3,2],[1,1,1]]
Output: 8
Explanation:
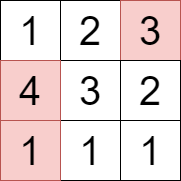
We can select the cells with values 1, 3, and 4 that are colored above.
Example 2
Input: grid = [[8,7,6],[8,3,2]]
Output: 15
Explanation:
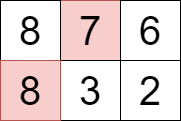
We can select the cells with values 7 and 8 that are colored above.
Constraints
1 <= grid.length, grid[i].length <= 101 <= grid[i][j] <= 100
Solution
Method 1 - DP with Bitmask (Enumerate Unique Values)
Intuition
We need to select at most one cell per row, and all selected values must be unique. Since grid values are small (≤100) and grid size is small (≤10x10), we can enumerate all subsets of unique values and try to assign them to rows using DP or backtracking.
Approach
- Collect all unique values in the grid.
- For each subset of unique values, try to assign each value to a row where it appears (no two values in the same row).
- For each subset, if assignment is possible, sum the values and update the answer.
- Use bitmask DP: dp[row][mask] = max sum for first 'row' rows, using values in 'mask'.
Code
C++
#include <vector>
#include <unordered_map>
#include <algorithm>
using namespace std;
class Solution {
public:
int maxScore(vector<vector<int>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> vals;
unordered_map<int, vector<int>> valRows;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
int v = grid[i][j];
if (valRows.count(v) == 0) vals.push_back(v);
valRows[v].push_back(i);
}
int U = vals.size(), res = 0;
for (int mask = 1; mask < (1<<U); ++mask) {
vector<int> used(m, 0);
int sum = 0, ok = 1;
for (int i = 0; i < U; ++i) if (mask & (1<<i)) {
int found = 0;
for (int r : valRows[vals[i]]) if (!used[r]) {
used[r] = 1; sum += vals[i]; found = 1; break;
}
if (!found) { ok = 0; break; }
}
if (ok) res = max(res, sum);
}
return res;
}
};
Go
func maxScore(grid [][]int) int {
m, n := len(grid), len(grid[0])
valRows := map[int][]int{}
vals := []int{}
for i := 0; i < m; i++ {
for j := 0; j < n; j++ {
v := grid[i][j]
if _, ok := valRows[v]; !ok { vals = append(vals, v) }
valRows[v] = append(valRows[v], i)
}
}
U, res := len(vals), 0
for mask := 1; mask < 1<<U; mask++ {
used := make([]bool, m)
sum, ok := 0, true
for i := 0; i < U; i++ {
if mask&(1<<i) > 0 {
found := false
for _, r := range valRows[vals[i]] {
if !used[r] { used[r] = true; sum += vals[i]; found = true; break }
}
if !found { ok = false; break }
}
}
if ok && sum > res { res = sum }
}
return res
}
Java
import java.util.*;
class Solution {
public int maxScore(int[][] grid) {
int m = grid.length, n = grid[0].length;
Map<Integer, List<Integer>> valRows = new HashMap<>();
List<Integer> vals = new ArrayList<>();
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
int v = grid[i][j];
if (!valRows.containsKey(v)) vals.add(v);
valRows.computeIfAbsent(v, k -> new ArrayList<>()).add(i);
}
int U = vals.size(), res = 0;
for (int mask = 1; mask < (1<<U); ++mask) {
boolean[] used = new boolean[m];
int sum = 0; boolean ok = true;
for (int i = 0; i < U; ++i) if ((mask & (1<<i)) > 0) {
boolean found = false;
for (int r : valRows.get(vals.get(i))) if (!used[r]) {
used[r] = true; sum += vals.get(i); found = true; break;
}
if (!found) { ok = false; break; }
}
if (ok) res = Math.max(res, sum);
}
return res;
}
}
Kotlin
class Solution {
fun maxScore(grid: Array<IntArray>): Int {
val m = grid.size
val n = grid[0].size
val valRows = mutableMapOf<Int, MutableList<Int>>()
val vals = mutableListOf<Int>()
for (i in 0 until m) for (j in 0 until n) {
val v = grid[i][j]
if (v !in valRows) vals.add(v)
valRows.getOrPut(v) { mutableListOf() }.add(i)
}
val U = vals.size
var res = 0
for (mask in 1 until (1 shl U)) {
val used = BooleanArray(m)
var sum = 0
var ok = true
for (i in 0 until U) if ((mask and (1 shl i)) != 0) {
var found = false
for (r in valRows[vals[i]]!!) if (!used[r]) {
used[r] = true; sum += vals[i]; found = true; break
}
if (!found) { ok = false; break }
}
if (ok) res = maxOf(res, sum)
}
return res
}
}
Python
def maxScore(grid):
m, n = len(grid), len(grid[0])
from collections import defaultdict
val_rows = defaultdict(list)
vals = []
for i in range(m):
for j in range(n):
v = grid[i][j]
if v not in val_rows:
vals.append(v)
val_rows[v].append(i)
U, res = len(vals), 0
for mask in range(1, 1<<U):
used = [0]*m
sumv, ok = 0, True
for i in range(U):
if mask & (1<<i):
found = False
for r in val_rows[vals[i]]:
if not used[r]:
used[r] = 1; sumv += vals[i]; found = True; break
if not found:
ok = False; break
if ok:
res = max(res, sumv)
return res
Rust
use std::collections::HashMap;
pub fn max_score(grid: Vec<Vec<i32>>) -> i32 {
let m = grid.len();
let n = grid[0].len();
let mut val_rows: HashMap<i32, Vec<usize>> = HashMap::new();
let mut vals = vec![];
for i in 0..m {
for j in 0..n {
let v = grid[i][j];
if !val_rows.contains_key(&v) { vals.push(v); }
val_rows.entry(v).or_default().push(i);
}
}
let U = vals.len();
let mut res = 0;
for mask in 1..(1<<U) {
let mut used = vec![false; m];
let mut sum = 0;
let mut ok = true;
for i in 0..U {
if (mask & (1<<i)) > 0 {
let mut found = false;
for &r in &val_rows[&vals[i]] {
if !used[r] { used[r] = true; sum += vals[i]; found = true; break; }
}
if !found { ok = false; break; }
}
}
if ok && sum > res { res = sum; }
}
res
}
TypeScript
function maxScore(grid: number[][]): number {
const m = grid.length, n = grid[0].length;
const valRows: Record<number, number[]> = {};
const vals: number[] = [];
for (let i = 0; i < m; ++i) for (let j = 0; j < n; ++j) {
const v = grid[i][j];
if (!(v in valRows)) vals.push(v);
if (!(v in valRows)) valRows[v] = [];
valRows[v].push(i);
}
const U = vals.length;
let res = 0;
for (let mask = 1; mask < (1<<U); ++mask) {
const used = Array(m).fill(false);
let sum = 0, ok = true;
for (let i = 0; i < U; ++i) if (mask & (1<<i)) {
let found = false;
for (const r of valRows[vals[i]]) {
if (!used[r]) { used[r] = true; sum += vals[i]; found = true; break; }
}
if (!found) { ok = false; break; }
}
if (ok && sum > res) res = sum;
}
return res;
}
Complexity
- ⏰ Time complexity:
O(2^U * U * m)where U = number of unique values (≤100), m = number of rows (≤10) - 🧺 Space complexity:
O(U + m)