Self Crossing

Problem

You are given an array of integers distance.

You start at the point (0, 0) on an X-Y plane, and you move distance[0] meters to the north, then distance[1] meters to the west, distance[2] meters to the south, distance[3] meters to the east, and so on. In other words, after each move, your direction changes counter-clockwise.

Return true if your path crosses itself or false if it does not.

You are given a sequence of positive numbers x_1, x_2, …, x_n (real-valued). Starting at the origin (0, 0), a traveler moves x_1 metres north, then x_2 metres west, then x_3 metres south, then x_4 metres east, and repeats the four-direction cycle counter-clockwise for the remaining distances.

Design a single-pass algorithm that uses O(1) extra memory to decide whether the traveler's path ever crosses itself (i.e., whether the polyline is self-intersecting).

Examples

Example 1

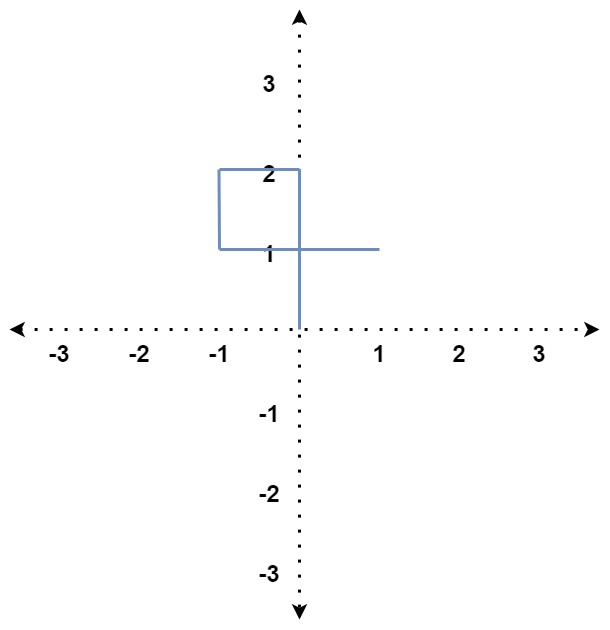
Input: distance = [2,1,1,2]
Output: true
Explanation: The path crosses itself at the point (0, 1).

Example 2

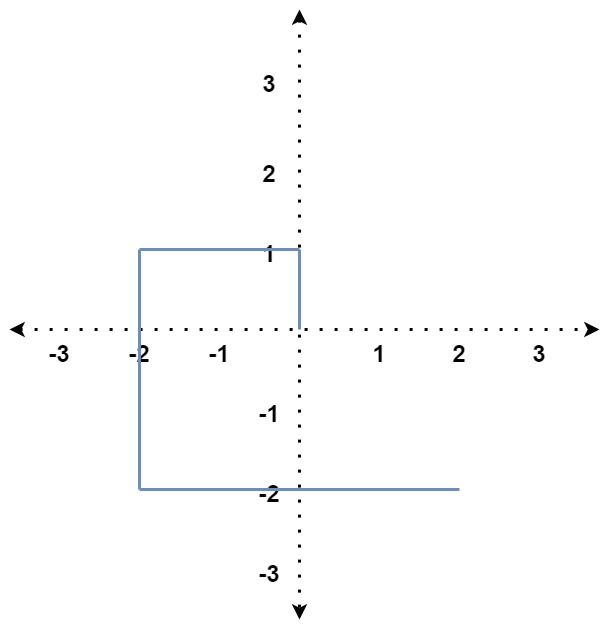
Input: distance = [1,2,3,4]
Output: false
Explanation: The path does not cross itself at any point.

Example 3

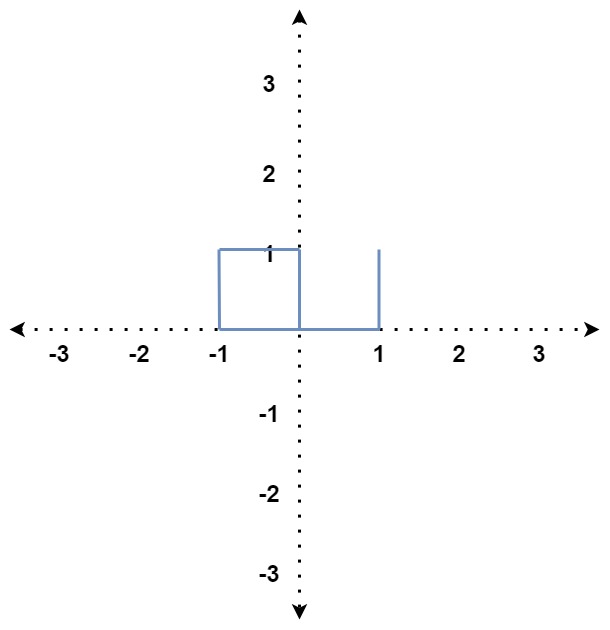
Input: distance = [1,1,1,2,1]
Output: true
Explanation: The path crosses itself at the point (0, 0).

Solution

Method 1 – Case Analysis (Three Crossing Patterns)

Intuition

As you walk in a counter-clockwise spiral, the path can only cross itself in three specific ways, based on the last 4, 5, or 6 moves. By checking these three cases at each step, we can detect any self-crossing efficiently.

Approach

Let the moves be denoted as x[0], x[1], x[2], ..., where:

x[0]: distance north
x[1]: distance west
x[2]: distance south
x[3]: distance east
... and so on, turning counter-clockwise after each move.

At each step i (starting from i = 3), we check for three possible crossing patterns:

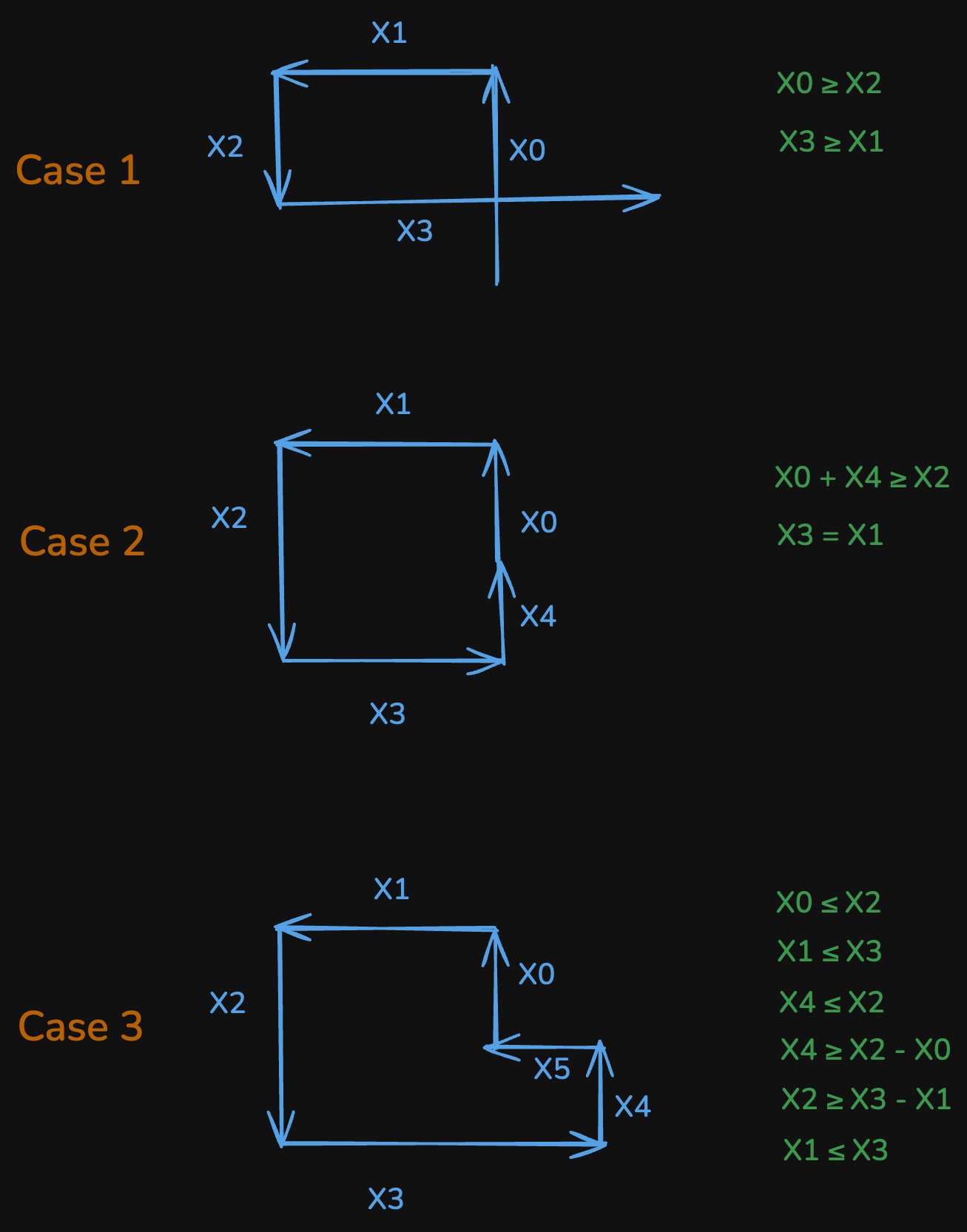
Case 1 (Fourth line crosses first):
- The current move x[i] crosses the segment x[i-3].
- Condition: x[i] >= x[i-2] and x[i-1] <= x[i-3]
- Visual: The path forms a simple loop, with the 4th segment crossing the 1st.
Case 2 (Fifth line meets first):
- The current move x[i] overlaps the segment x[i-4].
- Condition: i >= 4 and x[i-1] == x[i-3] and x[i] + x[i-4] >= x[i-2]
- Visual: The path touches or overlaps itself, with the 5th segment meeting the 1st.
Case 3 (Sixth line crosses first):
- The current move x[i] crosses the segment x[i-5].
- Condition: i >= 5 and all:
  - x[i-2] >= x[i-4]
  - x[i-1] <= x[i-3]
  - x[i-1] >= x[i-3] - x[i-5]
  - x[i] + x[i-4] >= x[i-2]
  - x[i-3] >= x[i-5]
- Visual: The path spirals in and the 6th segment crosses the 1st.

If any of these cases are true at any step, the path crosses itself. Otherwise, it does not.

Code

C++

class Solution {
public:
    bool isSelfCrossing(vector<int>& x) {
        int n = x.size();
        for (int i = 3; i < n; ++i) {
            if (x[i] >= x[i-2] && x[i-1] <= x[i-3]) return true;
            if (i >= 4 && x[i-1] == x[i-3] && x[i] + x[i-4] >= x[i-2]) return true;
            if (i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3] - x[i-5]
                && x[i] + x[i-4] >= x[i-2] && x[i-3] >= x[i-5]) return true;
        }
        return false;
    }
};

Go

func isSelfCrossing(x []int) bool {
    n := len(x)
    for i := 3; i < n; i++ {
        if x[i] >= x[i-2] && x[i-1] <= x[i-3] {
            return true
        }
        if i >= 4 && x[i-1] == x[i-3] && x[i]+x[i-4] >= x[i-2] {
            return true
        }
        if i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3]-x[i-5] && x[i]+x[i-4] >= x[i-2] && x[i-3] >= x[i-5] {
            return true
        }
    }
    return false
}

Java

class Solution {
    public boolean isSelfCrossing(int[] x) {
        int n = x.length;
        for (int i = 3; i < n; i++) {
            if (x[i] >= x[i-2] && x[i-1] <= x[i-3]) return true;
            if (i >= 4 && x[i-1] == x[i-3] && x[i] + x[i-4] >= x[i-2]) return true;
            if (i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3] - x[i-5]
                && x[i] + x[i-4] >= x[i-2] && x[i-3] >= x[i-5]) return true;
        }
        return false;
    }
}

Kotlin

class Solution {
    fun isSelfCrossing(x: IntArray): Boolean {
        val n = x.size
        for (i in 3 until n) {
            if (x[i] >= x[i-2] && x[i-1] <= x[i-3]) return true
            if (i >= 4 && x[i-1] == x[i-3] && x[i] + x[i-4] >= x[i-2]) return true
            if (i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3] - x[i-5]
                && x[i] + x[i-4] >= x[i-2] && x[i-3] >= x[i-5]) return true
        }
        return false
    }
}

Python

class Solution:
    def isSelfCrossing(self, x: list[int]) -> bool:
        n = len(x)
        for i in range(3, n):
            if x[i] >= x[i-2] and x[i-1] <= x[i-3]:
                return True
            if i >= 4 and x[i-1] == x[i-3] and x[i] + x[i-4] >= x[i-2]:
                return True
            if i >= 5 and x[i-2] >= x[i-4] and x[i-1] <= x[i-3] and x[i-1] >= x[i-3] - x[i-5] \
                and x[i] + x[i-4] >= x[i-2] and x[i-3] >= x[i-5]:
                return True
        return False

Rust

impl Solution {
    pub fn is_self_crossing(x: Vec<i32>) -> bool {
        let n = x.len();
        for i in 3..n {
            if x[i] >= x[i-2] && x[i-1] <= x[i-3] { return true; }
            if i >= 4 && x[i-1] == x[i-3] && x[i] + x[i-4] >= x[i-2] { return true; }
            if i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3] - x[i-5]
                && x[i] + x[i-4] >= x[i-2] && x[i-3] >= x[i-5] { return true; }
        }
        false
    }
}

TypeScript

class Solution {
    isSelfCrossing(x: number[]): boolean {
        const n = x.length;
        for (let i = 3; i < n; i++) {
            if (x[i] >= x[i-2] && x[i-1] <= x[i-3]) return true;
            if (i >= 4 && x[i-1] == x[i-3] && x[i] + x[i-4] >= x[i-2]) return true;
            if (i >= 5 && x[i-2] >= x[i-4] && x[i-1] <= x[i-3] && x[i-1] >= x[i-3] - x[i-5]
                && x[i] + x[i-4] >= x[i-2] && x[i-3] >= x[i-5]) return true;
        }
        return false;
    }
}

Complexity

⏰ Time complexity: O(n), where n is the number of moves.
🧺 Space complexity: O(1).