Problem

You are given a 2D integer array squares. Each squares[i] = [xi, yi, li] represents the coordinates of the bottom-left point and the side length of a square parallel to the x-axis.

Find the minimum y-coordinate value of a horizontal line such that the total area of the squares above the line equals the total area of the squares below the line.

Answers within 10-5 of the actual answer will be accepted.

Note : Squares may overlap. Overlapping areas should be counted multiple times.

Example 1

1
2
3
4
5
6

Input: squares = [[0,0,1],[2,2,1]]
Output: 1.00000
Explanation:
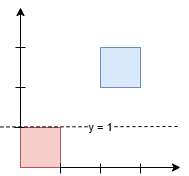
![](https://assets.leetcode.com/uploads/2025/01/06/4062example1drawio.png)
Any horizontal line between `y = 1` and `y = 2` will have 1 square unit above
it and 1 square unit below it. The lowest option is 1.

Example 2

1
2
3
4
5
6
7
8
9

Input: squares = [[0,0,2],[1,1,1]]
Output: 1.16667
Explanation:
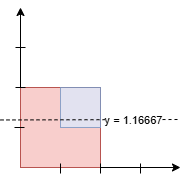
![](https://assets.leetcode.com/uploads/2025/01/15/4062example2drawio.png)
The areas are:
* Below the line: `7/6 * 2 (Red) + 1/6 (Blue) = 15/6 = 2.5`.
* Above the line: `5/6 * 2 (Red) + 5/6 (Blue) = 15/6 = 2.5`.
Since the areas above and below the line are equal, the output is `7/6 =
1.16667`.

Constraints

  • 1 <= squares.length <= 5 * 10^4
  • squares[i] = [xi, yi, li]
  • squares[i].length == 3
  • 0 <= xi, yi <= 10^9
  • 1 <= li <= 10^9
  • The total area of all the squares will not exceed 1012.

Examples

Solution

Method 1 – Binary Search + Direct Area Calculation

Intuition

Since overlapping areas are counted multiple times, the area below a line y is simply the sum of the area of each square below y. We can use binary search to find the minimum y where the area below is half the total area.

Approach

  1. For a given y, for each square, compute the area below y (if any part of the square is below y).
  2. Sum all such areas for all squares.
  3. Use binary search on y to find the value where the area below y is half the total area.
  4. Return the minimum such y.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    double separateSquares(vector<vector<int>>& squares) {
        auto area = [&](double y) -> double {
            double res = 0;
            for (auto& sq : squares) {
                double yl = sq[1], yr = sq[1] + sq[2];
                if (y <= yl) continue;
                double h = min(y, yr) - yl;
                if (h > 0) res += h * sq[2];
            }
            return res;
        };
        double total = 0;
        for (auto& sq : squares) total += sq[2] * sq[2];
        double l = 0, r = 1e9 + 1;
        for (int it = 0; it < 50; ++it) {
            double m = (l + r) / 2;
            if (area(m) * 2 < total) l = m;
            else r = m;
        }
        return l;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

class Solution {
    public double separateSquares(int[][] squares) {
        double total = 0;
        for (int[] sq : squares) total += (double)sq[2] * sq[2];
        double l = 0, r = 1e9 + 1;
        for (int it = 0; it < 50; ++it) {
            double m = (l + r) / 2;
            double area = 0;
            for (int[] sq : squares) {
                double yl = sq[1], yr = sq[1] + sq[2];
                if (m <= yl) continue;
                double h = Math.min(m, yr) - yl;
                if (h > 0) area += h * sq[2];
            }
            if (area * 2 < total) l = m;
            else r = m;
        }
        return l;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution:
    def separateSquares(self, squares: list[list[int]]) -> float:
        def area(y):
            res = 0
            for x, yl, l in squares:
                yr = yl + l
                if y <= yl:
                    continue
                h = min(y, yr) - yl
                if h > 0:
                    res += h * l
            return res
        total = sum(l * l for x, y, l in squares)
        l, r = 0, 1e9 + 1
        for _ in range(50):
            m = (l + r) / 2
            if area(m) * 2 < total:
                l = m
            else:
                r = m
        return l

Complexity

  • ⏰ Time complexity: O(n log M), where n = number of squares, M = search range. Each area computation is O(n), binary search is log M steps.
  • 🧺 Space complexity: O(1), as only a few variables are used.