problemhardalgorithmsleetcode-3515leetcode 3515leetcode3515

Shortest Path in a Weighted Tree

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

You are given an integer n and an undirected, weighted tree rooted at node 1 with n nodes numbered from 1 to n. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates an undirected edge from node ui to vi with weight wi.

You are also given a 2D integer array queries of length q, where each queries[i] is either:

  • [1, u, v, w'] - Update the weight of the edge between nodes u and v to w', where (u, v) is guaranteed to be an edge present in edges.
  • [2, x] - Compute the shortest path distance from the root node 1 to node x.

Return an integer array answer, where answer[i] is the shortest path distance from node 1 to x for the ith query of [2, x].

Examples

Example 1

Input: n = 2, edges = [[1,2,7]], queries = [[2,2],[1,1,2,4],[2,2]]
Output: [7,4]
Explanation:
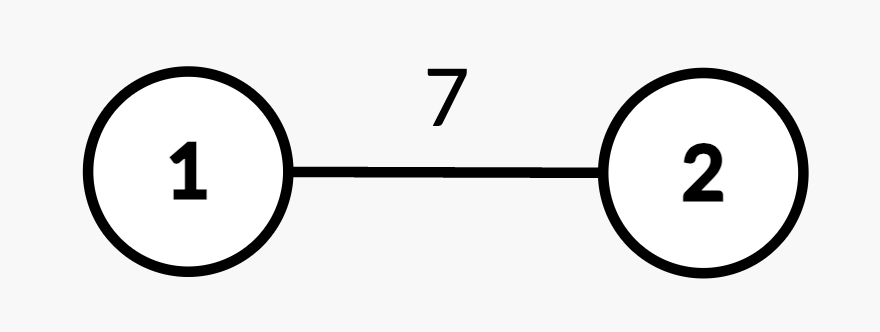
![](https://assets.leetcode.com/uploads/2025/03/13/screenshot-2025-03-13-at-133524.png)
* Query `[2,2]`: The shortest path from root node 1 to node 2 is 7.
* Query `[1,1,2,4]`: The weight of edge `(1,2)` changes from 7 to 4.
* Query `[2,2]`: The shortest path from root node 1 to node 2 is 4.

Example 2

Input: n = 3, edges = [[1,2,2],[1,3,4]], queries =
[[2,1],[2,3],[1,1,3,7],[2,2],[2,3]]
Output: [0,4,2,7]
Explanation:
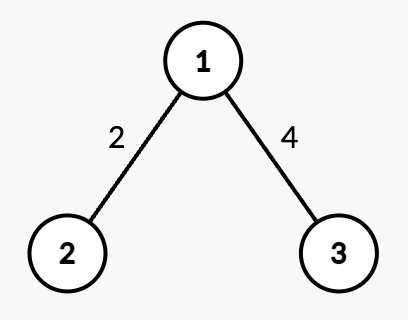
![](https://assets.leetcode.com/uploads/2025/03/13/screenshot-2025-03-13-at-132247.png)
* Query `[2,1]`: The shortest path from root node 1 to node 1 is 0.
* Query `[2,3]`: The shortest path from root node 1 to node 3 is 4.
* Query `[1,1,3,7]`: The weight of edge `(1,3)` changes from 4 to 7.
* Query `[2,2]`: The shortest path from root node 1 to node 2 is 2.
* Query `[2,3]`: The shortest path from root node 1 to node 3 is 7.

Example 3

Input: n = 4, edges = [[1,2,2],[2,3,1],[3,4,5]], queries =
[[2,4],[2,3],[1,2,3,3],[2,2],[2,3]]
Output: [8,3,2,5]
Explanation:
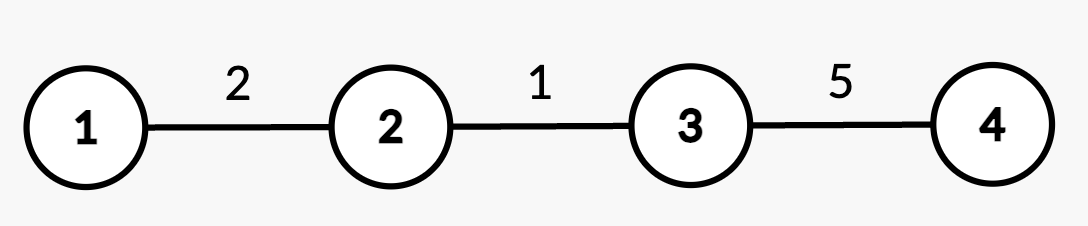
![](https://assets.leetcode.com/uploads/2025/03/13/screenshot-2025-03-13-at-133306.png)
* Query `[2,4]`: The shortest path from root node 1 to node 4 consists of edges `(1,2)`, `(2,3)`, and `(3,4)` with weights `2 + 1 + 5 = 8`.
* Query `[2,3]`: The shortest path from root node 1 to node 3 consists of edges `(1,2)` and `(2,3)` with weights `2 + 1 = 3`.
* Query `[1,2,3,3]`: The weight of edge `(2,3)` changes from 1 to 3.
* Query `[2,2]`: The shortest path from root node 1 to node 2 is 2.
* Query `[2,3]`: The shortest path from root node 1 to node 3 consists of edges `(1,2)` and `(2,3)` with updated weights `2 + 3 = 5`.

Constraints

  • 1 <= n <= 10^5
  • edges.length == n - 1
  • edges[i] == [ui, vi, wi]
  • 1 <= ui, vi <= n
  • 1 <= wi <= 10^4
  • The input is generated such that edges represents a valid tree.
  • 1 <= queries.length == q <= 10^5
  • queries[i].length == 2 or 4
    • queries[i] == [1, u, v, w'] or,
    • queries[i] == [2, x]
    • 1 <= u, v, x <= n
    • (u, v) is always an edge from edges.
    • 1 <= w' <= 10^4

Solution

Method 1 – Euler Tour + Binary Indexed Tree (Fenwick Tree)

Intuition

We need to support two operations efficiently:

  1. Update the weight of an edge.
  2. Query the shortest path from the root to any node.

Since the tree is rooted at 1, the shortest path from 1 to x is the sum of edge weights along the path. We can flatten the tree using an Euler tour, and use a Binary Indexed Tree (BIT) or Segment Tree to support fast range updates and point queries.

Approach

  1. Build the tree and assign each node an entry time (in-time) via DFS.
  2. For each edge, store its index and which child it connects to.
  3. Use a BIT to maintain the prefix sum of weights from the root to each node.
  4. For an update, update the BIT for the subtree of the child node.
  5. For a query, query the BIT at the in-time of the node.

Code

C++
#include <vector>
using namespace std;
class BIT {
    vector<long long> t; int n;
public:
    BIT(int sz): t(sz+2), n(sz+2) {}
    void add(int i, long long v) { for (; i < n; i += i&-i) t[i] += v; }
    long long sum(int i) { long long r=0; for (; i; i -= i&-i) r += t[i]; return r; }
    void range(int l, int r, long long v) { add(l, v); add(r+1, -v); }
};
class Solution {
public:
    vector<int> shortestPath(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {
        vector<vector<pair<int,int>>> g(n+1);
        map<pair<int,int>, int> edgeIdx;
        vector<int> eid(n+1), parent(n+1), in(n+1), out(n+1), weight(n);
        for (int i=0; i<edges.size(); ++i) {
            int u=edges[i][0], v=edges[i][1], w=edges[i][2];
            g[u].push_back({v,w}); g[v].push_back({u,w});
            edgeIdx[{u,v}] = edgeIdx[{v,u}] = i;
            weight[i] = w;
        }
        int time=1;
        function<void(int,int)> dfs = [&](int u, int p) {
            in[u]=time++;
            for (auto& [v,w]:g[u]) if (v!=p) {
                parent[v]=u;
                eid[v]=edgeIdx[{u,v}];
                dfs(v,u);
            }
            out[u]=time-1;
        };
        dfs(1,0);
        BIT bit(n+2);
        for (int v=2; v<=n; ++v) bit.range(in[v], in[v], weight[eid[v]]);
        vector<int> ans;
        for (auto& q:queries) {
            if (q[0]==1) {
                int u=q[1], v=q[2], w=q[3];
                int ch = parent[u]==v?u:v;
                int idx = eid[ch];
                int diff = w-weight[idx];
                bit.range(in[ch], out[ch], diff);
                weight[idx]=w;
            } else {
                int x=q[1];
                ans.push_back(bit.sum(in[x]));
            }
        }
        return ans;
    }
};
Java
import java.util.*;
class Solution {
    static class BIT {
        long[] t;
        int n;
        BIT(int sz) { t = new long[sz+2]; n = sz+2; }
        void add(int i, long v) { for (; i < n; i += i&-i) t[i] += v; }
        long sum(int i) { long r=0; for (; i>0; i -= i&-i) r += t[i]; return r; }
        void range(int l, int r, long v) { add(l, v); add(r+1, -v); }
    }
    public List<Integer> shortestPath(int n, int[][] edges, int[][] queries) {
        List<int[]>[] g = new List[n+1];
        for (int i=0; i<=n; ++i) g[i]=new ArrayList<>();
        Map<String,Integer> edgeIdx = new HashMap<>();
        int[] eid = new int[n+1], parent = new int[n+1], in = new int[n+1], out = new int[n+1], weight = new int[n];
        for (int i=0; i<edges.length; ++i) {
            int u=edges[i][0], v=edges[i][1], w=edges[i][2];
            g[u].add(new int[]{v,w}); g[v].add(new int[]{u,w});
            edgeIdx.put(u+","+v, i); edgeIdx.put(v+","+u, i);
            weight[i]=w;
        }
        int[] time = {1};
        dfs(1,0,g,parent,eid,edgeIdx,in,out,time);
        BIT bit = new BIT(n+2);
        for (int v=2; v<=n; ++v) bit.range(in[v], in[v], weight[eid[v]]);
        List<Integer> ans = new ArrayList<>();
        for (int[] q:queries) {
            if (q[0]==1) {
                int u=q[1], v=q[2], w=q[3];
                int ch = parent[u]==v?u:v;
                int idx = eid[ch];
                int diff = w-weight[idx];
                bit.range(in[ch], out[ch], diff);
                weight[idx]=w;
            } else {
                int x=q[1];
                ans.add((int)bit.sum(in[x]));
            }
        }
        return ans;
    }
    static void dfs(int u, int p, List<int[]>[] g, int[] parent, int[] eid, Map<String,Integer> edgeIdx, int[] in, int[] out, int[] time) {
        in[u]=time[0]++;
        for (int[] vw:g[u]) if (vw[0]!=p) {
            parent[vw[0]]=u;
            eid[vw[0]]=edgeIdx.get(u+","+vw[0]);
            dfs(vw[0],u,g,parent,eid,edgeIdx,in,out,time);
        }
        out[u]=time[0]-1;
    }
}
Python
class BIT:
    def __init__(self, n):
        self.n = n+2
        self.t = [0]*(self.n)
    def add(self, i, v):
        while i < self.n:
            self.t[i] += v
            i += i&-i
    def sum(self, i):
        r = 0
        while i:
            r += self.t[i]
            i -= i&-i
        return r
    def range(self, l, r, v):
        self.add(l, v)
        self.add(r+1, -v)

class Solution:
    def shortestPath(self, n, edges, queries):
        from collections import defaultdict
        g = defaultdict(list)
        edgeIdx = dict()
        weight = [0]*n
        for i, (u,v,w) in enumerate(edges):
            g[u].append((v,w))
            g[v].append((u,w))
            edgeIdx[(u,v)] = edgeIdx[(v,u)] = i
            weight[i] = w
        in_time = [0]*(n+1)
        out_time = [0]*(n+1)
        parent = [0]*(n+1)
        eid = [0]*(n+1)
        time = [1]
        def dfs(u, p):
            in_time[u]=time[0]
            time[0]+=1
            for v,w in g[u]:
                if v!=p:
                    parent[v]=u
                    eid[v]=edgeIdx[(u,v)]
                    dfs(v,u)
            out_time[u]=time[0]-1
        dfs(1,0)
        bit = BIT(n+2)
        for v in range(2,n+1):
            bit.range(in_time[v], in_time[v], weight[eid[v]])
        ans = []
        for q in queries:
            if q[0]==1:
                u,v,w = q[1:]
                ch = u if parent[u]==v else v
                idx = eid[ch]
                diff = w-weight[idx]
                bit.range(in_time[ch], out_time[ch], diff)
                weight[idx]=w
            else:
                x = q[1]
                ans.append(bit.sum(in_time[x]))
        return ans

Complexity

  • ⏰ Time complexity: O((n+q) log n) — Each update/query is O(log n), preprocessing is O(n).
  • 🧺 Space complexity: O(n) — For the tree, BIT, and auxiliary arrays.

Comments