Shortest Path Visiting All Nodes

Problem

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Examples

Example 1

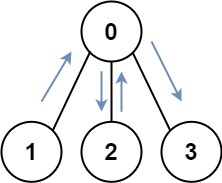
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2

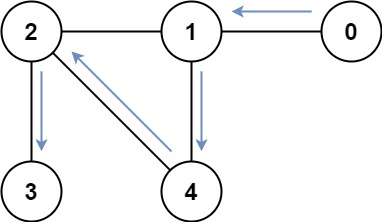
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Constraints

• n == graph.length
• 1 <= n <= 12
• 0 <= graph[i].length < n
• graph[i] does not contain i.
• If graph[a] contains b, then graph[b] contains a.
• The input graph is always connected.

Solution

Method 1 – BFS with Bitmask

Intuition

We need the shortest path that visits all nodes in a graph. Since revisiting nodes is allowed, and the number of nodes is small, we can use BFS with a bitmask to track visited nodes. Each state is defined by the current node and the set of visited nodes.

Approach

1. Use BFS starting from every node, with state (node, mask) where mask is a bitmask of visited nodes.
2. For each state, try all neighbors and update the mask.
3. If all nodes are visited (mask == (1<<n)-1), return the number of steps.
4. Use a queue for BFS and a set to avoid revisiting the same state.

Code

C++

class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();
        queue<pair<int, int>> q;
        vector<vector<int>> vis(n, vector<int>(1<<n, 0));
        for (int i = 0; i < n; ++i) {
            q.push({i, 1<<i});
            vis[i][1<<i] = 1;
        }
        int ans = 0;
        while (!q.empty()) {
            int sz = q.size();
            while (sz--) {
                auto [u, mask] = q.front(); q.pop();
                if (mask == (1<<n)-1) return ans;
                for (int v : graph[u]) {
                    int nxt = mask | (1<<v);
                    if (!vis[v][nxt]) {
                        vis[v][nxt] = 1;
                        q.push({v, nxt});
                    }
                }
            }
            ++ans;
        }
        return -1;
    }
};

Go

func shortestPathLength(graph [][]int) int {
    n := len(graph)
    type state struct{u, mask int}
    vis := make([][]bool, n)
    for i := range vis {
        vis[i] = make([]bool, 1<<n)
    }
    q := []state{}
    for i := 0; i < n; i++ {
        q = append(q, state{i, 1<<i})
        vis[i][1<<i] = true
    }
    ans := 0
    for len(q) > 0 {
        nq := []state{}
        for _, s := range q {
            if s.mask == (1<<n)-1 {
                return ans
            }
            for _, v := range graph[s.u] {
                nxt := s.mask | (1<<v)
                if !vis[v][nxt] {
                    vis[v][nxt] = true
                    nq = append(nq, state{v, nxt})
                }
            }
        }
        q = nq
        ans++
    }
    return -1
}

Java

class Solution {
    public int shortestPathLength(int[][] graph) {
        int n = graph.length;
        Queue<int[]> q = new LinkedList<>();
        boolean[][] vis = new boolean[n][1<<n];
        for (int i = 0; i < n; i++) {
            q.offer(new int[]{i, 1<<i});
            vis[i][1<<i] = true;
        }
        int ans = 0;
        while (!q.isEmpty()) {
            int sz = q.size();
            for (int i = 0; i < sz; i++) {
                int[] cur = q.poll();
                int u = cur[0], mask = cur[1];
                if (mask == (1<<n)-1) return ans;
                for (int v : graph[u]) {
                    int nxt = mask | (1<<v);
                    if (!vis[v][nxt]) {
                        vis[v][nxt] = true;
                        q.offer(new int[]{v, nxt});
                    }
                }
            }
            ans++;
        }
        return -1;
    }
}

Kotlin

class Solution {
    fun shortestPathLength(graph: Array<IntArray>): Int {
        val n = graph.size
        val vis = Array(n) { BooleanArray(1 shl n) }
        val q = ArrayDeque<Pair<Int, Int>>()
        for (i in 0 until n) {
            q.add(i to (1 shl i))
            vis[i][1 shl i] = true
        }
        var ans = 0
        while (q.isNotEmpty()) {
            repeat(q.size) {
                val (u, mask) = q.removeFirst()
                if (mask == (1 shl n) - 1) return ans
                for (v in graph[u]) {
                    val nxt = mask or (1 shl v)
                    if (!vis[v][nxt]) {
                        vis[v][nxt] = true
                        q.add(v to nxt)
                    }
                }
            }
            ans++
        }
        return -1
    }
}

Python

def shortestPathLength(graph: list[list[int]]) -> int:
    n = len(graph)
    from collections import deque
    vis = [[False]*(1<<n) for _ in range(n)]
    q = deque((i, 1<<i) for i in range(n))
    for i in range(n):
        vis[i][1<<i] = True
    ans = 0
    while q:
        for _ in range(len(q)):
            u, mask = q.popleft()
            if mask == (1<<n)-1:
                return ans
            for v in graph[u]:
                nxt = mask | (1<<v)
                if not vis[v][nxt]:
                    vis[v][nxt] = True
                    q.append((v, nxt))
        ans += 1
    return -1

Rust

use std::collections::VecDeque;
impl Solution {
    pub fn shortest_path_length(graph: Vec<Vec<i32>>) -> i32 {
        let n = graph.len();
        let mut vis = vec![vec![false; 1<<n]; n];
        let mut q = VecDeque::new();
        for i in 0..n {
            q.push_back((i, 1<<i));
            vis[i][1<<i] = true;
        }
        let mut ans = 0;
        while !q.is_empty() {
            for _ in 0..q.len() {
                let (u, mask) = q.pop_front().unwrap();
                if mask == (1<<n)-1 { return ans; }
                for &v in &graph[u] {
                    let nxt = mask | (1<<v);
                    if !vis[v as usize][nxt] {
                        vis[v as usize][nxt] = true;
                        q.push_back((v as usize, nxt));
                    }
                }
            }
            ans += 1;
        }
        -1
    }
}

TypeScript

class Solution {
    shortestPathLength(graph: number[][]): number {
        const n = graph.length;
        const vis: boolean[][] = Array.from({length: n}, () => Array(1<<n).fill(false));
        const q: [number, number][] = [];
        for (let i = 0; i < n; i++) {
            q.push([i, 1<<i]);
            vis[i][1<<i] = true;
        }
        let ans = 0;
        while (q.length) {
            const sz = q.length;
            for (let i = 0; i < sz; i++) {
                const [u, mask] = q.shift()!;
                if (mask === (1<<n)-1) return ans;
                for (const v of graph[u]) {
                    const nxt = mask | (1<<v);
                    if (!vis[v][nxt]) {
                        vis[v][nxt] = true;
                        q.push([v, nxt]);
                    }
                }
            }
            ans++;
        }
        return -1;
    }
}

Complexity

• ⏰ Time complexity: O(n*2^n), since there are n*2^n possible states.
• 🧺 Space complexity: O(n*2^n), for the visited states.