problemhardalgorithmsleetcode-2003leetcode 2003leetcode2003

Smallest Missing Genetic Value in Each Subtree

HardUpdated: Aug 2, 2025
Practice on:
LeetCode

Problem

There is a family tree rooted at 0 consisting of n nodes numbered 0 to n - 1. You are given a 0-indexed integer array parents, where parents[i] is the parent for node i. Since node 0 is the root , parents[0] == -1.

There are 105 genetic values, each represented by an integer in the inclusive range [1, 105]. You are given a 0-indexed integer array nums, where nums[i] is a distinct genetic value for node i.

Return an arrayans of lengthn whereans[i]is thesmallest genetic value that is missing from the subtree rooted at node i.

The subtree rooted at a node x contains node x and all of its descendant nodes.

Examples

Example 1


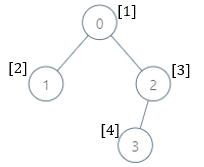
![](https://assets.leetcode.com/uploads/2021/08/23/case-1.png)

Input: parents = [-1,0,0,2], nums = [1,2,3,4]
Output: [5,1,1,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3] with values [1,2,3,4]. 5 is the smallest missing value.
- 1: The subtree contains only node 1 with value 2. 1 is the smallest missing value.
- 2: The subtree contains nodes [2,3] with values [3,4]. 1 is the smallest missing value.
- 3: The subtree contains only node 3 with value 4. 1 is the smallest missing value.

Example 2


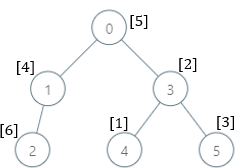
![](https://assets.leetcode.com/uploads/2021/08/23/case-2.png)

Input: parents = [-1,0,1,0,3,3], nums = [5,4,6,2,1,3]
Output: [7,1,1,4,2,1]
Explanation: The answer for each subtree is calculated as follows:
- 0: The subtree contains nodes [0,1,2,3,4,5] with values [5,4,6,2,1,3]. 7 is the smallest missing value.
- 1: The subtree contains nodes [1,2] with values [4,6]. 1 is the smallest missing value.
- 2: The subtree contains only node 2 with value 6. 1 is the smallest missing value.
- 3: The subtree contains nodes [3,4,5] with values [2,1,3]. 4 is the smallest missing value.
- 4: The subtree contains only node 4 with value 1. 2 is the smallest missing value.
- 5: The subtree contains only node 5 with value 3. 1 is the smallest missing value.

Example 3

Input: parents = [-1,2,3,0,2,4,1], nums = [2,3,4,5,6,7,8]
Output: [1,1,1,1,1,1,1]
Explanation: The value 1 is missing from all the subtrees.

Constraints

  • n == parents.length == nums.length
  • 2 <= n <= 10^5
  • 0 <= parents[i] <= n - 1 for i != 0
  • parents[0] == -1
  • parents represents a valid tree.
  • 1 <= nums[i] <= 10^5
  • Each nums[i] is distinct.

Solution

Method 1 – DFS from 1's Path (Efficient Subtree Marking)

Intuition

If 1 is not present in the tree, all answers are 1. Otherwise, only nodes on the path from the node with value 1 to the root can have answers greater than 1. We can use DFS to mark all genetic values in the subtree and incrementally find the smallest missing value.

Approach

  1. Build the tree as an adjacency list.
  2. Find the node with value 1. If not present, all answers are 1.
  3. For each node on the path from the node with value 1 to the root, do DFS to mark all genetic values in its subtree.
  4. For each such node, incrementally find the smallest missing value.
  5. For all other nodes, answer is 1.

Code

C++
#include <vector>
#include <unordered_set>
using namespace std;
class Solution {
public:
    vector<int> smallestMissingValueSubtree(vector<int>& parents, vector<int>& nums) {
        int n = parents.size();
        vector<vector<int>> g(n);
        for (int i = 1; i < n; ++i) g[parents[i]].push_back(i);
        vector<int> ans(n, 1);
        int pos = -1;
        for (int i = 0; i < n; ++i) if (nums[i] == 1) pos = i;
        if (pos == -1) return ans;
        vector<bool> seen(100002);
        int miss = 1;
        function<void(int)> dfs = [&](int u) {
            if (seen[nums[u]]) return;
            seen[nums[u]] = true;
            for (int v : g[u]) dfs(v);
        };
        for (int u = pos; u != -1; u = parents[u]) {
            dfs(u);
            while (seen[miss]) ++miss;
            ans[u] = miss;
        }
        return ans;
    }
};
Java
import java.util.*;
class Solution {
    public int[] smallestMissingValueSubtree(int[] parents, int[] nums) {
        int n = parents.length;
        List<Integer>[] g = new List[n];
        for (int i = 0; i < n; ++i) g[i] = new ArrayList<>();
        for (int i = 1; i < n; ++i) g[parents[i]].add(i);
        int[] ans = new int[n];
        Arrays.fill(ans, 1);
        int pos = -1;
        for (int i = 0; i < n; ++i) if (nums[i] == 1) pos = i;
        if (pos == -1) return ans;
        boolean[] seen = new boolean[100002];
        int miss = 1;
        Deque<Integer> stack = new ArrayDeque<>();
        // DFS implemented iteratively to avoid stack overflow
        for (int u = pos; u != -1; u = parents[u]) {
            stack.clear();
            stack.push(u);
            while (!stack.isEmpty()) {
                int node = stack.pop();
                if (seen[nums[node]]) continue;
                seen[nums[node]] = true;
                for (int v : g[node]) stack.push(v);
            }
            while (seen[miss]) ++miss;
            ans[u] = miss;
        }
        return ans;
    }
}
Python
class Solution:
    def smallestMissingValueSubtree(self, parents, nums):
        n = len(parents)
        g = [[] for _ in range(n)]
        for i in range(1, n):
            g[parents[i]].append(i)
        ans = [1] * n
        if 1 not in nums:
            return ans
        pos = nums.index(1)
        seen = set()
        miss = 1
        def dfs(u):
            if nums[u] in seen: return
            seen.add(nums[u])
            for v in g[u]:
                dfs(v)
        u = pos
        while u != -1:
            dfs(u)
            while miss in seen:
                miss += 1
            ans[u] = miss
            u = parents[u]
        return ans

Complexity

  • ⏰ Time complexity: O(n) — Each node is visited at most twice.
  • 🧺 Space complexity: O(n) — For the tree and seen set/array.

Comments