Problem

You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.

Return thelexicographically smallest string that starts at a leaf of this tree and ends at the root.

As a reminder, any shorter prefix of a string is lexicographically smaller.

  • For example, "ab" is lexicographically smaller than "aba".

A leaf of a node is a node that has no children.

Examples

Example 1

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2019/01/30/tree1.png)

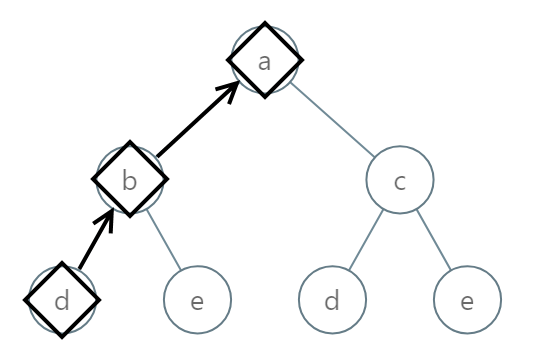
Input: root = [0,1,2,3,4,3,4]
Output: "dba"

Example 2

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2019/01/30/tree2.png)

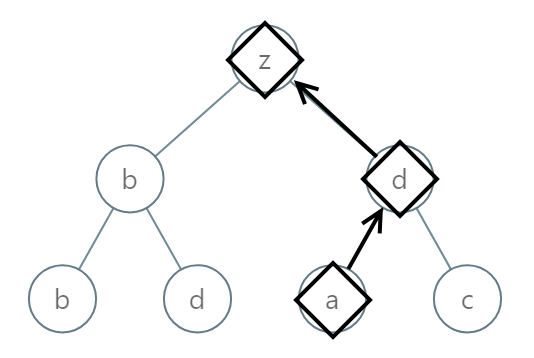
Input: root = [25,1,3,1,3,0,2]
Output: "adz"

Example 3

1
2
3
4
5


![](https://assets.leetcode.com/uploads/2019/02/01/tree3.png)

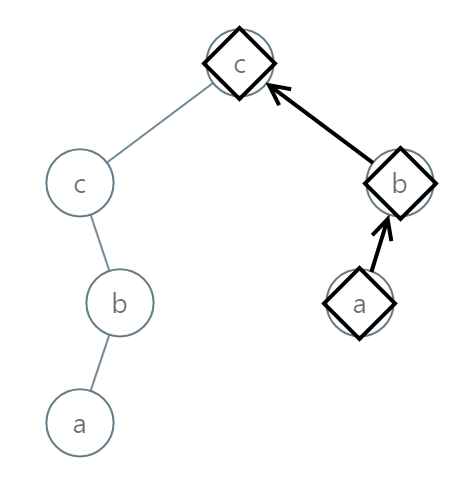
Input: root = [2,2,1,null,1,0,null,0]
Output: "abc"

Constraints

  • The number of nodes in the tree is in the range [1, 8500].
  • 0 <= Node.val <= 25

Solution

Method 1 – DFS with Path Tracking

Intuition

We want the lexicographically smallest string from any leaf to the root. We can use DFS to traverse all paths from leaves to root, building the string in reverse, and keep the smallest one found.

Approach

  1. Use DFS to traverse the tree, passing the current path (as a string or list).
  2. When a leaf is reached, build the string from leaf to root and compare with the current best.
  3. At each node, prepend the character for node.val to the path.
  4. Return the smallest string found.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

struct TreeNode { int val; TreeNode *left, *right; };
class Solution {
    string ans = "~";
    void dfs(TreeNode* node, string path) {
        if (!node) return;
        path = char('a' + node->val) + path;
        if (!node->left && !node->right) ans = min(ans, path);
        dfs(node->left, path);
        dfs(node->right, path);
    }
public:
    string smallestFromLeaf(TreeNode* root) {
        dfs(root, "");
        return ans;
    }
};
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

type TreeNode struct { Val int; Left, Right *TreeNode }
func smallestFromLeaf(root *TreeNode) string {
    ans := "~"
    var dfs func(*TreeNode, string)
    dfs = func(node *TreeNode, path string) {
        if node == nil { return }
        path = string('a'+node.Val) + path
        if node.Left == nil && node.Right == nil && path < ans { ans = path }
        dfs(node.Left, path)
        dfs(node.Right, path)
    }
    dfs(root, "")
    return ans
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class TreeNode { int val; TreeNode left, right; }
class Solution {
    String ans = "~";
    void dfs(TreeNode node, String path) {
        if (node == null) return;
        path = (char)('a'+node.val) + path;
        if (node.left == null && node.right == null && path.compareTo(ans) < 0) ans = path;
        dfs(node.left, path);
        dfs(node.right, path);
    }
    public String smallestFromLeaf(TreeNode root) {
        dfs(root, "");
        return ans;
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class TreeNode(var `val`: Int) { var left: TreeNode? = null; var right: TreeNode? = null }
class Solution {
    var ans = "~"
    fun dfs(node: TreeNode?, path: String) {
        if (node == null) return
        val p = ('a' + node.`val`).toChar() + path
        if (node.left == null && node.right == null && p < ans) ans = p
        dfs(node.left, p)
        dfs(node.right, p)
    }
    fun smallestFromLeaf(root: TreeNode?): String {
        dfs(root, "")
        return ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

class Solution:
    def smallestFromLeaf(self, root: 'TreeNode') -> str:
        ans = ['~']
        def dfs(node, path):
            if not node: return
            p = chr(ord('a') + node.val) + path
            if not node.left and not node.right:
                if p < ans[0]: ans[0] = p
            dfs(node.left, p)
            dfs(node.right, p)
        dfs(root, "")
        return ans[0]
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

use std::rc::Rc;
use std::cell::RefCell;
impl Solution {
    pub fn smallest_from_leaf(root: Option<Rc<RefCell<TreeNode>>>) -> String {
        fn dfs(node: Option<Rc<RefCell<TreeNode>>>, path: String, ans: &mut String) {
            if let Some(n) = node {
                let n = n.borrow();
                let mut p = (b'a' + n.val as u8) as char;
                let p = format!("{}{}", p, path);
                if n.left.is_none() && n.right.is_none() && p < *ans { *ans = p.clone(); }
                dfs(n.left.clone(), p.clone(), ans);
                dfs(n.right.clone(), p, ans);
            }
        }
        let mut ans = "~".to_string();
        dfs(root, String::new(), &mut ans);
        ans
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

class TreeNode { val: number; left: TreeNode | null; right: TreeNode | null; }
class Solution {
    smallestFromLeaf(root: TreeNode | null): string {
        let ans = "~";
        function dfs(node: TreeNode | null, path: string) {
            if (!node) return;
            const p = String.fromCharCode(97 + node.val) + path;
            if (!node.left && !node.right && p < ans) ans = p;
            dfs(node.left, p);
            dfs(node.right, p);
        }
        dfs(root, "");
        return ans;
    }
}

Complexity

  • ⏰ Time complexity: O(n*h), where n is the number of nodes and h is the height of the tree. Each path is built and compared.
  • 🧺 Space complexity: O(h), for the recursion stack and path string.