Problem

You are given an n x n integer matrix board where the cells are labeled from 1 to n^2 in a Boustrophedon style starting from the bottom left of the board (i.e. board[n - 1][0]) and alternating direction each row.

You start on square 1 of the board. In each move, starting from square curr, do the following:

  • Choose a destination square next with a label in the range [curr + 1, min(curr + 6, n^2)].
    • This choice simulates the result of a standard 6-sided die roll: i.e., there are always at most 6 destinations, regardless of the size of the board.
  • If next has a snake or ladder, you must move to the destination of that snake or ladder. Otherwise, you move to next.
  • The game ends when you reach the square n^2.

A board square on row r and column c has a snake or ladder if board[r][c] != -1. The destination of that snake or ladder is board[r][c]. Squares 1 and n^2 do not have a snake or ladder.

Note that you only take a snake or ladder at most once per move. If the destination to a snake or ladder is the start of another snake or ladder, you do not follow the subsequent snake or ladder.

  • For example, suppose the board is [[-1,4],[-1,3]], and on the first move, your destination square is 2. You follow the ladder to square 3, but do not follow the subsequent ladder to 4.

Return the least number of moves required to reach the square n^2. If it is not possible to reach the square, return -1.

Examples

Example 1:

1
2
3
4
5
6
7
8
9

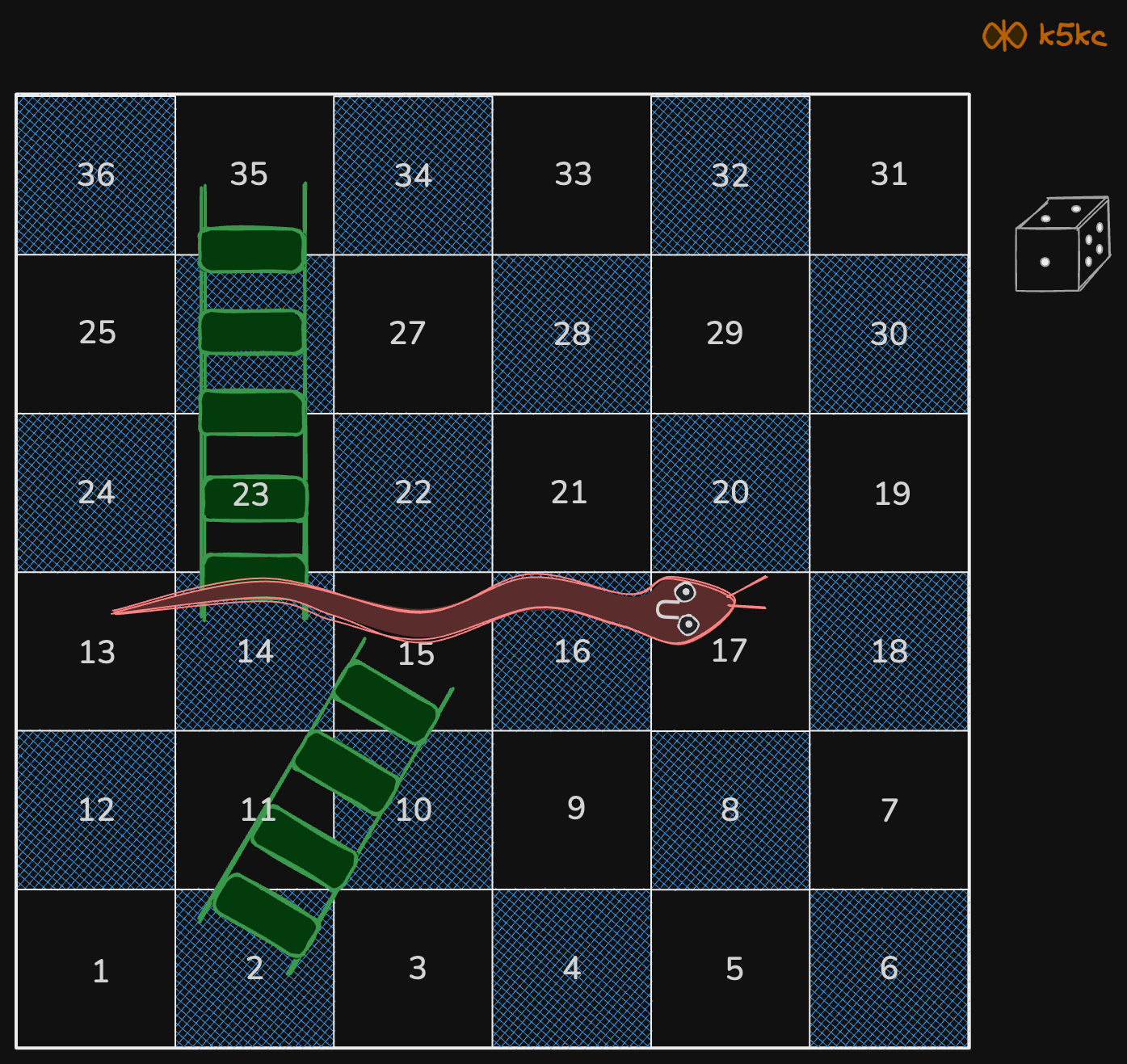
Input: board =[[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,-1,-1,-1,-1,-1],[-1,35,-1,-1,13,-1],[-1,-1,-1,-1,-1,-1],[-1,15,-1,-1,-1,-1]]
Output: 4
Explanation: 
In the beginning, you start at square 1 (at row 5, column 0).
You decide to move to square 2 and must take the ladder to square 15.
You then decide to move to square 17 and must take the snake to square 13.
You then decide to move to square 14 and must take the ladder to square 35.
You then decide to move to square 36, ending the game.
This is the lowest possible number of moves to reach the last square, so return 4.

Example 2:

1
2

Input: board =[[-1,-1],[-1,3]]
Output: 1

Solution

Method 1 - BFS

This approach efficiently solves the problem using BFS to find the minimum number of moves required to navigate from square 1 to square n^2 in a Boustrophedon-style board.

Here is approach:

  1. Label Conversion:
    • We need a way to convert from the linear square number (1 to (n^2)) to the 2D coordinates on the board.
  2. Breadth-First Search (BFS):
    • We start at square 1 and explore all possible next moves (up to 6 moves forward).
    • Keep track of visited squares to avoid cycles.
  3. Snakes and Ladders:
    • If a move lands on a square with a snake/ladder, directly move to the destination specified by that square.
  4. Termination:
    • The search ends once we reach square (n^2).

Here are the steps we can follow:

  1. Use a queue to perform BFS, starting from square 1.
  2. For each square, calculate all possible next moves (from 1 to 6 steps forward).
  3. Apply any snake or ladder effects.
  4. Continue until reaching (n^2) or exhausting all possible moves.

Code

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

public class Solution {
    // Convert the board position from number to 2D coordinates
    private int[] convertToCoordinates(int num, int n) {
        int row = (num - 1) / n;
        int col = (num - 1) % n;
        if (row % 2 == 1) { // Boustrophedon - reverse row order
            col = n - 1 - col;
        }
        row = n - 1 - row;
        return new int[] {row, col};
    }

    public int snakesAndLadders(int[][] board) {
        int n = board.length;
        int target = n * n;
        boolean[] visited = new boolean[n * n + 1];
        Queue<int[]> queue = new LinkedList<>();
        queue.offer(new int[] {1, 0}); // {current square, number of moves}

        while (!queue.isEmpty()) {
            int[] curr = queue.poll();
            int square = curr[0];
            int moves = curr[1];

            if (square == target) {
                return moves;
            }

            for (int nextSquare = square + 1;
                 nextSquare <= Math.min(square + 6, target); nextSquare++) {
                int[] pos = convertToCoordinates(nextSquare, n);
                int nextRow = pos[0];
                int nextCol = pos[1];

                int finalSquare = nextSquare;
                if (board[nextRow][nextCol] != -1) {
                    finalSquare = board[nextRow][nextCol];
                }

                if (!visited[finalSquare]) {
                    visited[finalSquare] = true;
                    queue.offer(new int[] {finalSquare, moves + 1});
                }
            }
        }

        return -1; // If we exhaust all possibilities and do not reach target
    }
}
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

from collections import deque


def get_board_value(board, n, num):
    quot, rem = divmod(num - 1, n)
    row = n - 1 - quot
    col = rem if quot % 2 == 0 else n - 1 - rem
    return board[row][col]


def snakesAndLadders(board):
    n = len(board)
    end_value = n * n
    visited = set()
    queue = deque([(1, 0)])  # (square, moves)

    while queue:
        square, moves = queue.popleft()
        if square == end_value:
            return moves
        for i in range(1, 7):
            next_square = square + i
            if next_square <= end_value:
                row, col = get_board_value(board, n, next_square)
                if col != -1:
                    next_square = col
                if next_square not in visited:
                    visited.add(next_square)
                    queue.append((next_square, moves + 1))

    return -1

Complexity

  • ⏰ Time complexity: O(n^2), where (n) is the dimension of the board. Each node (square) can be visited once, and each node has at most 6 neighboring nodes.
  • 🧺 Space complexity: O(n^2), due to the queue and visited set.